GlobalPointer:用统一的方式处理嵌套和非嵌套NER
By 苏剑林 | 2021-05-01 | 493298位读者 |(注:本文的相关内容已整理成论文《Global Pointer: Novel Efficient Span-based Approach for Named Entity Recognition》,如需引用可以直接引用英文论文,谢谢。)
本文将介绍一个称为GlobalPointer的设计,它利用全局归一化的思路来进行命名实体识别(NER),可以无差别地识别嵌套实体和非嵌套实体,在非嵌套(Flat NER)的情形下它能取得媲美CRF的效果,而在嵌套(Nested NER)情形它也有不错的效果。还有,在理论上,GlobalPointer的设计思想就比CRF更合理;而在实践上,它训练的时候不需要像CRF那样递归计算分母,预测的时候也不需要动态规划,是完全并行的,理想情况下时间复杂度是$\mathcal{O}(1)$!
简单来说,就是更漂亮、更快速、更强大!真有那么好的设计吗?不妨继续看看。
GlobalPointer #
常规的Pointer Network的设计在做实体识别或者阅读理解时,一般是用两个模块分别识别实体的首和尾,这会带来训练和预测时的不一致。而GlobalPointer就是针对这个不一致而设计的,它将首尾视为一个整体去进行判别,所以它更有“全局观”(更Global)。
基本思路 #
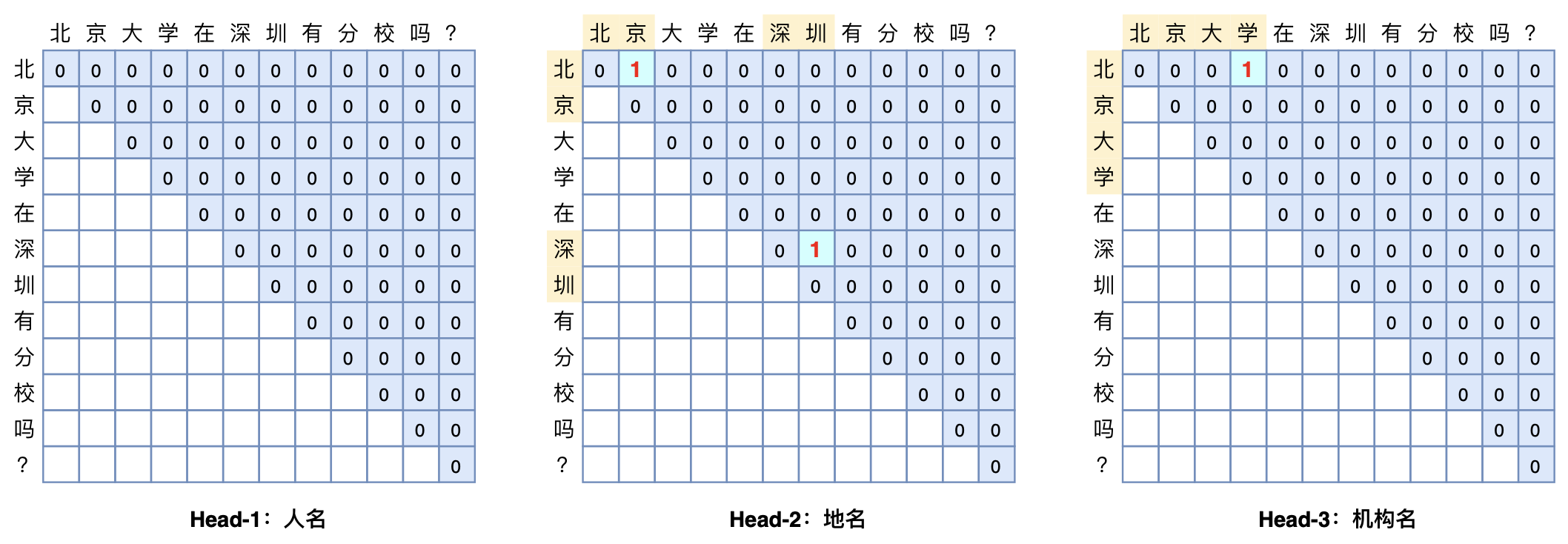
具体来说,假设要识别文本序列长度为$n$,简单起见先假定只有一种实体要识别,并且假定每个待识别实体是该序列的一个连续片段,长度不限,并且可以相互嵌套(两个实体之间有交集),那么该序列有多少个“候选实体”呢?不难得出,答案是$n(n+1)/2$个,即长度为$n$的序列有$n(n+1)/2$个不同的连续子序列,这些子序列包含了所有可能的实体,而我们要做的就是从这$n(n+1)/2$个“候选实体”里边挑出真正的实体,其实就是一个“$n(n+1)/2$选$k$”的多标签分类问题。如果有$m$种实体类型需要识别,那么就做成$m$个“$n(n+1)/2$选$k$”的多标签分类问题。这就是GlobalPointer的基本思想,以实体为基本单位进行判别,如本文开头的图片所示。
可能有读者会问:这种设计的复杂度明明就是$\mathcal{O}(n^2)$呀,不会特别慢吗?如果现在还是RNN/CNN的时代,那么它可能就显得很慢了,但如今是Transformer遍布NLP的时代,Transformer的每一层都是$\mathcal{O}(n^2)$的复杂度,多GlobalPointer一层不多,少GlobalPointer一层也不少,关键是$\mathcal{O}(n^2)$的复杂度仅仅是空间复杂度,如果并行性能好的话,时间复杂度甚至可以降到$\mathcal{O}(1)$,所以不会有明显感知。
数学形式 #
设长度为$n$的输入$t$经过编码后得到向量序列$[\boldsymbol{h}_1,\boldsymbol{h}_2,\cdots,\boldsymbol{h}_n]$,通过变换$\boldsymbol{q}_{i,\alpha}=\boldsymbol{W}_{q,\alpha}\boldsymbol{h}_i+\boldsymbol{b}_{q,\alpha}$和$\boldsymbol{k}_{i,\alpha}=\boldsymbol{W}_{k,\alpha}\boldsymbol{h}_i+\boldsymbol{b}_{k,\alpha}$我们可以得到序列向量序列$[\boldsymbol{q}_{1,\alpha},\boldsymbol{q}_{2,\alpha},\cdots,\boldsymbol{q}_{n,\alpha}]$和$[\boldsymbol{k}_{1,\alpha},\boldsymbol{k}_{2,\alpha},\cdots,\boldsymbol{k}_{n,\alpha}]$,它们是识别第$\alpha$种类型实体所用的向量序列。此时我们可以定义
\begin{equation}s_{\alpha}(i,j) = \boldsymbol{q}_{i,\alpha}^{\top}\boldsymbol{k}_{j,\alpha}\label{eq:s}\end{equation}
作为从$i$到$j$的连续片段是一个类型为$\alpha$的实体的打分。也就是说,用$\boldsymbol{q}_{i,\alpha}$与$\boldsymbol{k}_{j,\alpha}$的内积,作为片段$t_{[i:j]}$是类型为$\alpha$的实体的打分(logits),这里的$t_{[i:j]}$指的是序列$t$的第$i$个到第$j$个元素组成的连续子串。在这样的设计下,GlobalPointer事实上就是Multi-Head Attention的一个简化版而已,有多少种实体就对应多少个head,相比Multi-Head Attention去掉了$\boldsymbol{V}$相关的运算。
相对位置 #
理论上来说,式$\eqref{eq:s}$这样的设计就足够了,但实际上训练语料比较有限的情况下,它的表现往往欠佳,因为它没有显式地包含相对位置信息。在后面的实验中我们将会看到,加不加相对位置信息,效果可以相差30个百分点以上!
比如,我们要识别出地名,输入是天气预报的内容“北京:21度;上海:22度;杭州:23度;广州:24度;...”,这时候要识别出来的实体有很多,如果没有相对位置信息输入的话,GlobalPointer对实体的长度和跨度都不是特别敏感,因此很容易把任意两个实体的首尾组合都当成目标预测出来(即预测出“北京:21度;上海”这样的实体)。相反,有了相对位置信息之后,GlobalPointer就会对实体的长度和跨度比较敏感,因此能更好地分辨出真正的实体出来。
用哪种相对位置编码呢?理论上来说,Transformer里边所有的相对位置编码都可以考虑用(参考《让研究人员绞尽脑汁的Transformer位置编码》),但真的要去落实就会发现一个问题,大多数相对位置编码都对相对位置进行了一个截断,虽然这个截断范围对我们要识别的实体来说基本都够用了,但未免有点不优雅,不截断又会面临可学参数太多的问题。想来想去,还是觉得笔者之前构思的旋转式位置编码(RoPE)比较适合。
RoPE的介绍可见《Transformer升级之路:2、博采众长的旋转式位置编码》,它其实就是一个变换矩阵$\boldsymbol{\mathcal{R}}_i$,满足关系$\boldsymbol{\mathcal{R}}_i^{\top}\boldsymbol{\mathcal{R}}_j = \boldsymbol{\mathcal{R}}_{j-i}$,这样一来我们分别应用到$\boldsymbol{q},\boldsymbol{k}$中,就有
\begin{equation}s_{\alpha}(i,j) = (\boldsymbol{\mathcal{R}}_i\boldsymbol{q}_{i,\alpha})^{\top}(\boldsymbol{\mathcal{R}}_j\boldsymbol{k}_{j,\alpha}) = \boldsymbol{q}_{i,\alpha}^{\top} \boldsymbol{\mathcal{R}}_i^{\top}\boldsymbol{\mathcal{R}}_j\boldsymbol{k}_{j,\alpha} = \boldsymbol{q}_{i,\alpha}^{\top} \boldsymbol{\mathcal{R}}_{j-i}\boldsymbol{k}_{j,\alpha}\end{equation}
从而就显式地往打分$s_{\alpha}(i,j)$注入了相对位置信息。
优化细节 #
在这部分内容中,我们会讨论关于GlobalPointer在训练过程中的一些细节问题,包括损失函数的选择以及评价指标的计算和优化等,从中我们可以看到,GlobalPointer以实体为单位的设计有着诸多优雅和便利之处。
损失函数 #
到目前为止,我们已经设计好了打分$s_{\alpha}(i,j)$,识别特定的类$\alpha$的实体,则变成了共有$n(n+1)/2$类的多标签分类问题。接下来的关键是损失函数的设计。最朴素的思路是变成$n(n+1)/2$个二分类,然而实际使用时$n$往往并不小,那么$n(n+1)/2$更大,而每个句子的实体数不会很多(每一类的实体数目往往只是个位数),所以如果是$n(n+1)/2$个二分类的话,会带来极其严重的类别不均衡问题。
这时候我们之前研究的《将“Softmax+交叉熵”推广到多标签分类问题》就可以派上用场了。简单来说,这是一个用于多标签分类的损失函数,它是单目标多分类交叉熵的推广,特别适合总类别数很大、目标类别数较小的多标签分类问题。其形式也不复杂,在GlobalPointer的场景,它为
\begin{equation}\log \left(1 + \sum\limits_{(i,j)\in P_{\alpha}} e^{-s_{\alpha}(i,j)}\right) + \log \left(1 + \sum\limits_{(i,j)\in Q_{\alpha}} e^{s_{\alpha}(i,j)}\right)\end{equation}
其中$P_{\alpha}$是该样本的所有类型为$\alpha$的实体的首尾集合,$Q_{\alpha}$是该样本的所有非实体或者类型非$\alpha$的实体的首尾集合,注意我们只需要考虑$i\leq j$的组合,即
\begin{equation}\begin{aligned}
\Omega=&\,\big\{(i,j)\,\big|\,1\leq i\leq j\leq n\big\}\\
P_{\alpha}=&\,\big\{(i,j)\,\big|\,t_{[i:j]}\text{是类型为}\alpha\text{的实体}\big\}\\
Q_{\alpha}=&\,\Omega - P_{\alpha}
\end{aligned}\end{equation}
而在解码阶段,所有满足$s_{\alpha}(i,j) > 0$的片段$t_{[i:j]}$都被视为类型为$\alpha$的实体输出。可见,解码过程是及其简单的,并且在充分并行下解码效率就是$\mathcal{O}(1)$!
评价指标 #
对于NER来说,常见的评价指标就是F1,注意是实体级别的F1,并非标注标签级别的F1。在传统的Pointer Network或者CRF的设计下,我们并不容易在训练过程中直接计算实体级别的F1,但是在GlobalPointer的设计下,不管是计算实体级别的F1还是accuracy都是很容易的,比如F1的计算如下:
def global_pointer_f1_score(y_true, y_pred):
"""给GlobalPointer设计的F1
"""
y_pred = K.cast(K.greater(y_pred, 0), K.floatx())
return 2 * K.sum(y_true * y_pred) / K.sum(y_true + y_pred)能有这么简单,主要就是因为GlobalPointer的“Global”,它的y_true和y_pred本身就已经是实体级别了,通过y_pred > 0我们就可以知道哪些实体被抽取出来的,然后做个匹配就可以算出各种(实体级别的)指标,达到了训练、评估、预测的一致性。
优化F1值 #
GlobalPointer的“Global”还有一个好处,就是如果我们用它来做阅读理解的话,它可以直接优化阅读理解的F1指标!阅读理解的F1跟NER的F1有所不同,它是答案的一个模糊匹配程度,直接优化F1可能更有利于提高阅读理解的最终得分。将GlobalPointer用于阅读理解,相当于就只有一种实体类型的NER,此时我们定义
\begin{equation}p(i,j) = \frac{e^{s(i,j)}}{\sum\limits_{i \leq j} e^{s(i,j)}}\end{equation}
而有了$p(i,j)$之后,用强化学习的思想(参考《殊途同归的策略梯度与零阶优化》),优化F1就是以下述函数为损失:
\begin{equation}-\sum_{i\leq j} p(i,j) f_1(i,j) + \lambda \sum_{i\leq j}p(i,j)\log p(i,j)\end{equation}
这里的$f_1(i,j)$就是提前算好的片段$t_{[i:j]}$与标准答案之间的F1相似度,$\lambda$是一个超参数。当然,算出所有的$f_1(i,j)$成本可能会有点大,但它是一次性的,而且可以在计算时做些策略(比如首尾差别过大就直接置零),总的来说,可以控制在能接受的范围。如果为了提高阅读理解最终的F1,这是一种比较直接的可以尝试的方案。(笔者在今年的百度lic2021阅读理解赛道上尝试过,确实能有一定的效果。)
实验结果 #
现在一切准备就绪,马上就能够开始实验了,实验代码整理如下:
目前GlobalPointer已经内置在bert4keras>=0.10.6中,bert4keras的用户可以直接升级bert4keras使用。实验的三个任务均为中文NER任务,前两个为非嵌套NER,第三个为嵌套NER,它们的训练集文本长度统计信息为:
\begin{array}{c|cc}
\hline
& \text{平均字数} & \text{字数标准差} \\
\hline
\text{人民日报NER} & 46.93 & 30.08\\
\text{CLUENER} & 37.38 & 10.71\\
\text{CMeEE} & 54.15 & 80.27\\
\hline
\end{array}
人民日报 #
首先,我们验证一下在非嵌套场景GlobalPointer能否取代CRF,语料是经典的人民日报语料,baseline是BERT+CRF的组合,而对比的是BERT+GlobalPointer的组合,实验结果如下:
\begin{array}{c}
\text{人民日报NER实验结果} \\
{\begin{array}{c|cc|cc}
\hline
& \text{验证集F1} & \text{测试集F1} & \text{训练速度} & \text{预测速度}\\
\hline
\text{CRF} & 96.39\% & 95.46\% & 1\text{x} & 1\text{x}\\
\text{GlobalPointer (w/o RoPE)} & 54.35\% & 62.59\% & 1.61\text{x} & 1.13\text{x} \\
\text{GlobalPointer (w/ RoPE)}& 96.25\% & 95.51\% & 1.56\text{x} & 1.11\text{x} \\
\hline
\end{array}}
\end{array}
首先,表格中带来最大视觉冲击力的无疑是GlobalPointer有无RoPE的差距,达到了30个点以上!这说明了给GlobalPointer显式加入相对位置信息的重要性,后面的实验中我们将不再验证去掉RoPE的版本,默认都加上RoPE。
从表格中还可以看出,在经典的非嵌套NER任务中,效果上GlobalPointer可以跟CRF相媲美,速度上GlobalPointer还更胜一筹,称得上是又快又好了。
CLUENER #
当然,可能因为人民日报这个经典任务的起点已经很高了,所以拉不开差距。为此,我们在测一下比较新的CLUENER数据集,这个数据集也是非嵌套的,当前SOTA的F1是81%左右。BERT+CRF与BERT+GlobalPointer的对比如下:
\begin{array}{c}
\text{CLUENER实验结果} \\
{\begin{array}{c|cc|cc}
\hline
& \text{验证集F1} & \text{测试集F1} & \text{训练速度} & \text{预测速度}\\
\hline
\text{CRF} & 79.51\% & 78.70\% & 1\text{x} & 1\text{x}\\
\text{GlobalPointer}& 80.03\% & 79.44\% & 1.22\text{x} & 1\text{x} \\
\hline
\end{array}}
\end{array}
这个实验结果说明了,当NER难度增加之后,哪怕只是非嵌套的场景,GlobalPointer的效果能优于CRF,这说明对于NER场景,GlobalPointer其实比CRF更加好用。后面我们将对此做个简单的理论分析,进一步说明GlobalPointer相比CRF在理论上就更加合理。
至于速度方面,由于这个任务的文本长度普遍较短,因此GlobalPointer的速度增幅也没有那么明显。
CMeEE #
最后,我们来测一个嵌套的任务(CMeEE),它是去年biendata上的“中文医学文本命名实体识别”比赛,也是今年的“中文医疗信息处理挑战榜CBLUE”的任务1,简单来说就是医学方面的NER,带有一定的嵌套实体。同样比较CRF和GlobalPointer的效果:
\begin{array}{c}
\text{CMeEE实验结果} \\
{\begin{array}{c|cc|cc}
\hline
& \text{验证集F1} & \text{测试集F1} & \text{训练速度} & \text{预测速度}\\
\hline
\text{CRF} & 63.81\% & 64.39\% & 1\text{x} & 1\text{x}\\
\text{GlobalPointer}& 64.84\% & 65.98\% & 1.52\text{x} & 1.13\text{x} \\
\hline
\end{array}}
\end{array}
可以看到效果上GlobalPointer明显地优于CRF;速度方面,综合三个任务的结果,总的来说文本越长的任务,GlobalPointer的训练加速就越明显,而预测速度通常也略有提升,但幅度没有训练阶段大。随后笔者以RoBERTa large为encoder继续捣鼓了一下,发现线上测试集就可以(不是太难地)达到67%以上,这说明GlobalPointer是一个“称职”的设计了。
当然,可能有读者会诟病:你拿非嵌套的CRF去做嵌套的NER,这样跟GlobalPointer比肯定不公平呀。确实会有点,但是问题不大,一方面CMeEE目前的F1还比较低,嵌套的实体本来就不多,哪怕去掉嵌套部分当成非嵌套的来做,影响也不会太大;另一方面就是在嵌套NER方面,笔者还没发现比较简单明快的设计可以作为baseline跑跑的,所以就还是先跑个CRF看看了。欢迎读者报告其他设计的对比结果。
思考拓展 #
在本节中,我们将进一步对CRF和GlobalPointer做一个理论上的对比,并且介绍一些与GlobalPointer相关的工作,以方便读者更好地理解和定位GlobalPointer。
相比CRF #
CRF(条件随机场,Conditional Random Field)是序列标注的经典设计,由于大多数NER也能转化为序列标注问题,所以CRF也算是NER的经典方法,笔者也曾撰写过《简明条件随机场CRF介绍(附带纯Keras实现)》和《你的CRF层的学习率可能不够大》等文章来介绍CRF。在之前的介绍中,我们介绍过,如果序列标注的标签数为$k$,那么逐帧softmax和CRF的区别在于:
前者将序列标注看成是$n$个$k$分类问题,后者将序列标注看成是$1$个$k^n$分类问题。
这句话事实上也说明了逐帧softmax和CRF用于NER时的理论上的缺点。怎么理解呢?逐帧softmax将序列标注看成是$n$个$k$分类问题,那是过于宽松了,因为某个位置上的标注标签预测对了,不代表实体就能正确抽取出来了,起码有一个片段的标签都对了才算对;相反,CRF将序列标注看成是$1$个$k^n$分类问题,则又过于严格了,因为这意味着它要求所有实体都预测正确才算对,只对部分实体也不给分。虽然实际使用中我们用CRF也能出现部分正确的预测结果,但那只能说明模型本身的泛化能力好,CRF本身的设计确实包含了“全对才给分”的意思。
所以,CRF在理论上确实都存在不大合理的地方,而相比之下,GlobalPointer则更加贴近使用和评测场景:它本身就是以实体为单位的,并且它设计为一个“多标签分类”问题,这样它的损失函数和评价指标都是实体颗粒度的,哪怕只对一部分也得到了合理的打分。因此,哪怕在非嵌套NER场景,GlobalPointer能取得比CRF好也是“情理之中”的。
相关工作 #
如果读者比较关注实体识别、信息抽取的进展,那么应该可以发现,GlobalPointer与前段时间的关系抽取新设计TPLinker很相似。但事实上,这种全局归一化的思想,还可以追溯到更远。
对于笔者来说,第一次了解到这种思想,是在百度2017年发表的一篇《Globally Normalized Reader》,里边提出了一种用于阅读理解的全局归一化设计(GNR),里边不单单将(首, 尾)视为一个整体了,而是(句子, 首, 尾)视为一个整体(它是按照先选句子,然后在句子中选首尾的流程,所以多了一个句子维度),这样一来组合数就非常多了,因此它还用了《Sequence-to-Sequence Learning as Beam-Search Optimization》里边的思路来降低计算量。
有了GNR作铺垫,其实GlobalPointer就很容易可以想到的,事实上早在前年笔者在做LIC2019的关系抽取赛道的时候,类似的想法就已经有了,但是当时还有几个问题没有解决。
第一,当时Transformer还没有流行起来,总觉得$\mathcal{O}(n^2)$的复杂度很可怕;第二,当时《将“Softmax+交叉熵”推广到多标签分类问题》也还没想出来,所以多标签分类的不均衡问题没有很好的解决方案;第三,当时笔者对NLP各方面的理解也还浅,bert4keras也没开发,一旦实验起来束手束脚的,出现问题也不知道往哪里调(比如开始没加上RoPE,降低了30个点以上,如果是两年前,我肯定没啥调优方案了)。
所以,GlobalPointer算是这两年来笔者经过各方面积累后的一个有点“巧合”但又有点“水到渠成”的工作。至于TPLinker,它还真跟GlobalPointer起源没什么直接联系。当然,在形式上GlobalPointer确实跟TPLinker很相似,事实上TPLinker还可以追溯到更早的《Joint entity recognition and relation extraction as a multi-head selection problem》,只不过这系列文章都主要是把这种Global的思想用于关系抽取了,没有专门针对NER优化。
加性乘性 #
在具体实现上,TPLinker与GlobalPointer的一个主要区别是在Multi-Head上TPLinker用的是加性Attention:
\begin{equation}s_{\alpha}(i,j) = \boldsymbol{W}_{o,\alpha}\tanh\left(\boldsymbol{W}_{h,\alpha}[\boldsymbol{h}_{i},\boldsymbol{h}_{j}]+\boldsymbol{b}_{h,\alpha}\right)+\boldsymbol{b}_{o,\alpha}
\end{equation}
目前尚不清楚该选择与式$\eqref{eq:s}$的效果差异有多大,但是相比式$\eqref{eq:s}$的乘性Attention,虽然它们的理论复杂度相似,但实际实现上这种加性Attention的计算成本会大很多,尤其是空间成本(显存)会大很多~
所以笔者认为,就算加性效果确实比乘性好一些,也应该选择在乘性的基础上继续优化才行,因为加性的效率确实不行啊。此外,TPLinker等文章也没有像本文一样报告过相对位置信息的重要性,难道在加性Attention中相对位置不那么重要了?这些暂时还不得而知。
本文小结 #
本文介绍了一种NER的新设计GlobalPointer,它基于全局指针的思想,融合了笔者之前的一些研究结果,实现了用统一的方式处理嵌套和非嵌套NER的“理想设计”。实验结果显示,在非嵌套的情形下它能取得媲美CRF的效果,而在嵌套情形它也有不错的效果。
转载到请包括本文地址:https://kexue.fm/archives/8373
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (May. 01, 2021). 《GlobalPointer:用统一的方式处理嵌套和非嵌套NER 》[Blog post]. Retrieved from https://kexue.fm/archives/8373
@online{kexuefm-8373,
title={GlobalPointer:用统一的方式处理嵌套和非嵌套NER},
author={苏剑林},
year={2021},
month={May},
url={\url{https://kexue.fm/archives/8373}},
}










February 7th, 2022
请问是否可以提供阅读理解任务对应的损失的代码实现呢?
https://github.com/bojone/CLUE-bert4keras/blob/master/src/cmrc2018.py
感谢!
February 14th, 2022
按苏神的经验,用lstm做embedding,LSTM+GP效果会优于LSTM+CRF吗
会的
尝试了LSTM,BERT,ALBERT,LSTM,IDCNN,TextCNN等encoder,搭配GP和CRF,CRF仅在搭配IDCNN时和GP打成平手,其他encoder均是GP明显胜出。数据有偏差,仅供参考;
不好意思,没有TextCNN:p
感谢提供结果。
March 31st, 2022
请问有公式6对应的损失函数的代码吗,自己实现的训练时会梯度溢出
$\log$没加$\epsilon$吧?
April 2nd, 2022
苏神,你感觉对于有多个span(实体)需要抽取的类MRC任务,公式(6)可以直接套用吗,还是需要进行修改?因为直觉上两个实体的情况下总的 P=1 好像不太对?
这个不能,它只适用于答案只有一个的情况。
April 21st, 2022
有论文地址吗
April 26th, 2022
请问现在方案支持单字提取吗?效果如何?
如:我想听骁
做了实验,现有方案可以提取单字,效果比CRF好。
肯定可以的,没有限制实体的长度。
May 10th, 2022
苏神,想问您一下,为啥我用globalpointer跑biendata中文医学文本命名实体识别的效果还不如crf,想让您帮我看下啥原因
我掐指算了几算,依然算不出什么原因。施主可否再提供多一点信息?
就是globalpoint按苏神您的代码写的,但是就是不知道为啥识别出来的结果,像症状sym这种长实体很多都识别成了短实体,还不如crf,而且大致看了些带有几个嵌套的语句,也没识别出来嵌套实体,不知道是啥原因,代码感觉没错。f1值只有0.60,我的模型是roberta+bilstm+globalpoint,害
你是自己用别的语言复现的?cmeee这个任务?看看别人有没有实现好的对照一下?另外去掉lstm试试?
请问您去掉LSTM试了嘛,效果怎么样呢,最终你是选择搭了哪些模型框架呀
May 15th, 2022
请问,这种loss函数由考虑长尾分布吗?(最近看到一个工作,设计了针对不同类型的适应性阈值,并嵌入到了焦点损失函数中,来解决类别不均衡问题,当然,它是在关系识别任务中,但NER中应该也会存在不均衡的问题吧)
不知道你说的是什么不均衡。
May 24th, 2022
苏神你好,请问 “如果有m种实体类型需要识别,那么就做成m个“n(n+1)/2选k”的多标签分类问题” 这里m种实体类型是否可以做成n(n+1)/2个softmax多分类(类别数=m)?
可以做成$n(n+1)/2$个$m+1$分类(因为要多出一类“非实体”),但这样做的话,非实体类的样本就会非常多,于是有严重的类别不平衡问题。
在这篇文章,作者对实体识别做的就是上面老哥评论的(m+1)分类,但是作者实际训练时没有对所有的span进行分类,用了正样本和随机提取的一些负样本。针对深苏神回复的类别不平衡问题,苏神觉得这种做法是一个比较好的解决方案吗?
论文地址:https://static.aminer.cn/storage/pdf/arxiv/19/1909/1909.07755.pdf
“随机提取的一些负样本”那就是普通的过采样技术了,或许有效,但没什么新鲜的,从我自己的审美而言,算不上“比较好”。
June 8th, 2022
呃,评论被吞了吗?
请问苏神,如果将GP得到的token-pair网格得分,后接softmax函数(相当于对每个网格单元做m分类,m是类别),然后再用些focal_loss 或者 减轻负样本损失权重等方法,效果会不会比现在的更好?
可能可以达到相近的效果,但是大规模超过应该很难了。另外本文所提的loss可以认为无参数的了,像focal loss或者其他类似方法,有超参数要调,也是一件麻烦事。