生成扩散模型漫谈(三):DDPM = 贝叶斯 + 去噪
By 苏剑林 | 2022-07-19 | 272879位读者 |到目前为止,笔者给出了生成扩散模型DDPM的两种推导,分别是《生成扩散模型漫谈(一):DDPM = 拆楼 + 建楼》中的通俗类比方案和《生成扩散模型漫谈(二):DDPM = 自回归式VAE》中的变分自编码器方案。两种方案可谓各有特点,前者更为直白易懂,但无法做更多的理论延伸和定量理解,后者理论分析上更加完备一些,但稍显形式化,启发性不足。
在这篇文章中,我们再分享DDPM的一种推导,它主要利用到了贝叶斯定理来简化计算,整个过程的“推敲”味道颇浓,很有启发性。不仅如此,它还跟我们后面将要介绍的DDIM模型有着紧密的联系。
模型绘景 #
再次回顾,DDPM建模的是如下变换流程:
\begin{equation}\boldsymbol{x} = \boldsymbol{x}_0 \rightleftharpoons \boldsymbol{x}_1 \rightleftharpoons \boldsymbol{x}_2 \rightleftharpoons \cdots \rightleftharpoons \boldsymbol{x}_{T-1} \rightleftharpoons \boldsymbol{x}_T = \boldsymbol{z}\end{equation}
其中,正向就是将样本数据$\boldsymbol{x}$逐渐变为随机噪声$\boldsymbol{z}$的过程,反向就是将随机噪声$\boldsymbol{z}$逐渐变为样本数据$\boldsymbol{x}$的过程,反向过程就是我们希望得到的“生成模型”。
正向过程很简单,每一步是
\begin{equation}\boldsymbol{x}_t = \alpha_t \boldsymbol{x}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t,\quad \boldsymbol{\varepsilon}_t\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\end{equation}
或者写成$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})=\mathcal{N}(\boldsymbol{x}_t;\alpha_t \boldsymbol{x}_{t-1},\beta_t^2 \boldsymbol{I})$。在约束$\alpha_t^2 + \beta_t^2 = 1$之下,我们有
\begin{equation}\begin{aligned}
\boldsymbol{x}_t =&\, \alpha_t \boldsymbol{x}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t \\
=&\, \alpha_t \big(\alpha_{t-1} \boldsymbol{x}_{t-2} + \beta_{t-1} \boldsymbol{\varepsilon}_{t-1}\big) + \beta_t \boldsymbol{\varepsilon}_t \\
=&\,\cdots\\
=&\,(\alpha_t\cdots\alpha_1) \boldsymbol{x}_0 + \underbrace{(\alpha_t\cdots\alpha_2)\beta_1 \boldsymbol{\varepsilon}_1 + (\alpha_t\cdots\alpha_3)\beta_2 \boldsymbol{\varepsilon}_2 + \cdots + \alpha_t\beta_{t-1} \boldsymbol{\varepsilon}_{t-1} + \beta_t \boldsymbol{\varepsilon}_t}_{\sim \mathcal{N}(\boldsymbol{0}, (1-\alpha_t^2\cdots\alpha_1^2)\boldsymbol{I})}
\end{aligned}\end{equation}
从而可以求出$p(\boldsymbol{x}_t|\boldsymbol{x}_0)=\mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0,\bar{\beta}_t^2 \boldsymbol{I})$,其中$\bar{\alpha}_t = \alpha_1\cdots\alpha_t$,而$\bar{\beta}_t = \sqrt{1-\bar{\alpha}_t^2}$。
DDPM要做的事情,就是从上述信息中求出反向过程所需要的$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$,这样我们就能实现从任意一个$\boldsymbol{x}_T=\boldsymbol{z}$出发,逐步采样出$\boldsymbol{x}_{T-1},\boldsymbol{x}_{T-2},\cdots,\boldsymbol{x}_1$,最后得到随机生成的样本数据$\boldsymbol{x}_0=\boldsymbol{x}$。
请贝叶斯 #
下面我们请出伟大的贝叶斯定理。事实上,直接根据贝叶斯定理我们有
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) = \frac{p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})p(\boldsymbol{x}_{t-1})}{p(\boldsymbol{x}_t)}\label{eq:bayes}\end{equation}
然而,我们并不知道$p(\boldsymbol{x}_{t-1}),p(\boldsymbol{x}_t)$的表达式,所以此路不通。但我们可以退而求其次,在给定$\boldsymbol{x}_0$的条件下使用贝叶斯定理:
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \frac{p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)}{p(\boldsymbol{x}_t|\boldsymbol{x}_0)}\end{equation}
这样修改自然是因为$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1}),p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0),p(\boldsymbol{x}_t|\boldsymbol{x}_0)$都是已知的,所以上式是可计算的,代入各自的表达式得到:
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \mathcal{N}\left(\boldsymbol{x}_{t-1};\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\boldsymbol{x}_0,\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)\label{eq:p-xt-x0}\end{equation}
推导:上式的推导过程并不难,就是常规的展开整理而已,当然我们也可以找点技巧加快计算。首先,代入各自的表达式,可以发现指数部分除掉$-1/2$因子外,结果是:
\begin{equation}\frac{\Vert \boldsymbol{x}_t - \alpha_t \boldsymbol{x}_{t-1}\Vert^2}{\beta_t^2} + \frac{\Vert \boldsymbol{x}_{t-1} - \bar{\alpha}_{t-1}\boldsymbol{x}_0\Vert^2}{\bar{\beta}_{t-1}^2} - \frac{\Vert \boldsymbol{x}_t - \bar{\alpha}_t \boldsymbol{x}_0\Vert^2}{\bar{\beta}_t^2}\end{equation}
它关于$\boldsymbol{x}_{t-1}$是二次的,因此最终的分布必然也是正态分布,我们只需要求出其均值和协方差。不难看出,展开式中$\Vert \boldsymbol{x}_{t-1}\Vert^2$项的系数是
\begin{equation}\frac{\alpha_t^2}{\beta_t^2} + \frac{1}{\bar{\beta}_{t-1}^2} = \frac{\alpha_t^2\bar{\beta}_{t-1}^2 + \beta_t^2}{\bar{\beta}_{t-1}^2 \beta_t^2} = \frac{\alpha_t^2(1-\bar{\alpha}_{t-1}^2) + \beta_t^2}{\bar{\beta}_{t-1}^2 \beta_t^2} = \frac{1-\bar{\alpha}_t^2}{\bar{\beta}_{t-1}^2 \beta_t^2} = \frac{\bar{\beta}_t^2}{\bar{\beta}_{t-1}^2 \beta_t^2}\end{equation}
所以整理好的结果必然是$\frac{\bar{\beta}_t^2}{\bar{\beta}_{t-1}^2 \beta_t^2}\Vert \boldsymbol{x}_{t-1} - \tilde{\boldsymbol{\mu}}(\boldsymbol{x}_t, \boldsymbol{x}_0)\Vert^2$的形式,这意味着协方差矩阵是$\frac{\bar{\beta}_{t-1}^2 \beta_t^2}{\bar{\beta}_t^2}\boldsymbol{I}$。另一边,把一次项系数拿出来是$-2\left(\frac{\alpha_t}{\beta_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}}{\bar{\beta}_{t-1}^2}\boldsymbol{x}_0 \right)$,除以$\frac{-2\bar{\beta}_t^2}{\bar{\beta}_{t-1}^2 \beta_t^2}$后便可以得到
\begin{equation}\tilde{\boldsymbol{\mu}}(\boldsymbol{x}_t, \boldsymbol{x}_0)=\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\boldsymbol{x}_0 \end{equation}
这就得到了$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$的所有信息了,结果正是式$\eqref{eq:p-xt-x0}$。
去噪过程 #
现在我们得到了$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$,它有显式的解,但并非我们想要的最终答案,因为我们只想通过$\boldsymbol{x}_t$来预测$\boldsymbol{x}_{t-1}$,而不能依赖$\boldsymbol{x}_0$,$\boldsymbol{x}_0$是我们最终想要生成的结果。接下来,一个“异想天开”的想法是
如果我们能够通过$\boldsymbol{x}_t$来预测$\boldsymbol{x}_0$,那么不就可以消去$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$中的$\boldsymbol{x}_0$,使得它只依赖于$\boldsymbol{x}_t$了吗?
说干就干,我们用$\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$来预估$\boldsymbol{x}_0$,损失函数为$\Vert \boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)\Vert^2$。训练完成后,我们就认为
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t),\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)\label{eq:p-xt}\end{equation}
在$\Vert \boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)\Vert^2$中,$\boldsymbol{x}_0$代表原始数据,$\boldsymbol{x}_t$代表带噪数据,所以这实际上在训练一个去噪模型,这也就是DDPM的第一个“D”的含义(Denoising)。
具体来说,$p(\boldsymbol{x}_t|\boldsymbol{x}_0)=\mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0,\bar{\beta}_t^2 \boldsymbol{I})$意味着$\boldsymbol{x}_t = \bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon},\boldsymbol{\varepsilon}\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$,或者写成$\boldsymbol{x}_0 = \frac{1}{\bar{\alpha}_t}\left(\boldsymbol{x}_t - \bar{\beta}_t \boldsymbol{\varepsilon}\right)$,这启发我们将$\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$参数化为
\begin{equation}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t) = \frac{1}{\bar{\alpha}_t}\left(\boldsymbol{x}_t - \bar{\beta}_t \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right)\label{eq:bar-mu}\end{equation}
此时损失函数变为
\begin{equation}\Vert \boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)\Vert^2 = \frac{\bar{\beta}_t^2}{\bar{\alpha}_t^2}\left\Vert\boldsymbol{\varepsilon} - \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}, t)\right\Vert^2\end{equation}
省去前面的系数,就得到DDPM原论文所用的损失函数了。可以发现,本文是直接得出了从$\boldsymbol{x}_t$到$\boldsymbol{x}_0$的去噪过程,而不是像之前两篇文章那样,通过$\boldsymbol{x}_t$到$\boldsymbol{x}_{t-1}$的去噪过程再加上积分变换来推导,相比之下本文的推导可谓更加一步到位了。
另一边,我们将式$\eqref{eq:bar-mu}$代入到式$\eqref{eq:p-xt}$中,化简得到
\begin{equation}
p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \frac{\beta_t^2}{\bar{\beta}_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right),\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)\end{equation}
这就是反向的采样过程所用的分布,连同采样过程所用的方差也一并确定下来了。至此,DDPM推导完毕~(注:出于推导的流畅性考虑,本文的$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}$跟前两篇介绍不一样,反而跟DDPM原论文一致。)
推导:将式$\eqref{eq:bar-mu}$代入到式$\eqref{eq:p-xt}$的主要化简难度就是计算
\begin{equation}\begin{aligned}\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2} + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\alpha}_t\bar{\beta}_t^2} =&\, \frac{\alpha_t\bar{\beta}_{t-1}^2 + \beta_t^2/\alpha_t}{\bar{\beta}_t^2} = \frac{\alpha_t^2(1-\bar{\alpha}_{t-1}^2) + \beta_t^2}{\alpha_t\bar{\beta}_t^2} = \frac{1-\bar{\alpha}_t^2}{\alpha_t\bar{\beta}_t^2} = \frac{1}{\alpha_t}
\end{aligned}\end{equation}
预估修正 #
不知道读者有没有留意到一个有趣的地方:我们要做的事情,就是想将$\boldsymbol{x}_T$慢慢地变为$\boldsymbol{x}_0$,而我们在借用$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$近似$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$时,却包含了“用$\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$来预估$\boldsymbol{x}_0$”这一步,要是能预估准的话,那就直接一步到位了,还需要逐步采样吗?
真实情况是,“用$\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$来预估$\boldsymbol{x}_0$”当然不会太准的,至少开始的相当多步内不会太准。它仅仅起到了一个前瞻性的预估作用,然后我们只用$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$来推进一小步,这就是很多数值算法中的“预估-修正”思想,即我们用一个粗糙的解往前推很多步,然后利用这个粗糙的结果将最终结果推进一小步,以此来逐步获得更为精细的解。
由此我们还可以联想到Hinton三年前提出的《Lookahead Optimizer: k steps forward, 1 step back》,它同样也包含了预估(k steps forward)和修正(1 step back)两部分,原论文将其诠释为“快(Fast)-慢(Slow)”权重的相互结合,快权重就是预估得到的结果,慢权重则是基于预估所做的修正结果。如果愿意,我们也可以用同样的方式去诠释DDPM的“预估-修正”过程~
遗留问题 #
最后,在使用贝叶斯定理一节中,我们说式$\eqref{eq:bayes}$没法直接用的原因是$p(\boldsymbol{x}_{t-1})$和$p(\boldsymbol{x}_t)$均不知道。因为根据定义,我们有
\begin{equation}p(\boldsymbol{x}_t) = \int p(\boldsymbol{x}_t|\boldsymbol{x}_0)\tilde{p}(\boldsymbol{x}_0)d\boldsymbol{x}_0\end{equation}
其中$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$是知道的,而数据分布$\tilde{p}(\boldsymbol{x}_0)$无法提前预知,所以不能进行计算。不过,有两个特殊的例子,是可以直接将两者算出来的,这里我们也补充计算一下,其结果也正好是上一篇文章遗留的方差选取问题的答案。
第一个例子是整个数据集只有一个样本,不失一般性,假设该样本为$\boldsymbol{0}$,此时$\tilde{p}(\boldsymbol{x}_0)$为狄拉克分布$\delta(\boldsymbol{x}_0)$,可以直接算出$p(\boldsymbol{x}_t)=p(\boldsymbol{x}_t|\boldsymbol{0})$。继而代入式$\eqref{eq:bayes}$,可以发现结果正好是$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0)$取$\boldsymbol{x}_0=\boldsymbol{0}$的特例,即
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) = p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\boldsymbol{0}) = \mathcal{N}\left(\boldsymbol{x}_{t-1};\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t,\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)\end{equation}
我们主要关心其方差为$\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}$,这便是采样方差的选择之一。
第二个例子是数据集服从标准正态分布,即$\tilde{p}(\boldsymbol{x}_0)=\mathcal{N}(\boldsymbol{x}_0;\boldsymbol{0},\boldsymbol{I})$。前面我们说了$p(\boldsymbol{x}_t|\boldsymbol{x}_0)=\mathcal{N}(\boldsymbol{x}_t;\bar{\alpha}_t \boldsymbol{x}_0,\bar{\beta}_t^2 \boldsymbol{I})$意味着$\boldsymbol{x}_t = \bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon},\boldsymbol{\varepsilon}\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$,而此时根据假设还有$\boldsymbol{x}_0\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$,所以由正态分布的叠加性,$\boldsymbol{x}_t$正好也服从标准正态分布。将标准正态分布的概率密度代入式$\eqref{eq:bayes}$后,结果的指数部分除掉$-1/2$因子外,结果是:
\begin{equation}\frac{\Vert \boldsymbol{x}_t - \alpha_t \boldsymbol{x}_{t-1}\Vert^2}{\beta_t^2} + \Vert \boldsymbol{x}_{t-1}\Vert^2 - \Vert \boldsymbol{x}_t\Vert^2\end{equation}
跟推导$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0)$的过程类似,可以得到上述指数对应于
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) = \mathcal{N}\left(\boldsymbol{x}_{t-1};\alpha_t\boldsymbol{x}_t,\beta_t^2 \boldsymbol{I}\right)\end{equation}
我们同样主要关心其方差为$\beta_t^2$,这便是采样方差的另一个选择。
文章小结 #
本文分享了DDPM的一种颇有“推敲”味道的推导,它借助贝叶斯定理来直接推导反向的生成过程,相比之前的“拆楼-建楼”类比和变分推断理解更加一步到位。同时,它也更具启发性,跟接下来要介绍的DDIM有很密切的联系。
转载到请包括本文地址:https://kexue.fm/archives/9164
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jul. 19, 2022). 《生成扩散模型漫谈(三):DDPM = 贝叶斯 + 去噪 》[Blog post]. Retrieved from https://kexue.fm/archives/9164
@online{kexuefm-9164,
title={生成扩散模型漫谈(三):DDPM = 贝叶斯 + 去噪},
author={苏剑林},
year={2022},
month={Jul},
url={\url{https://kexue.fm/archives/9164}},
}







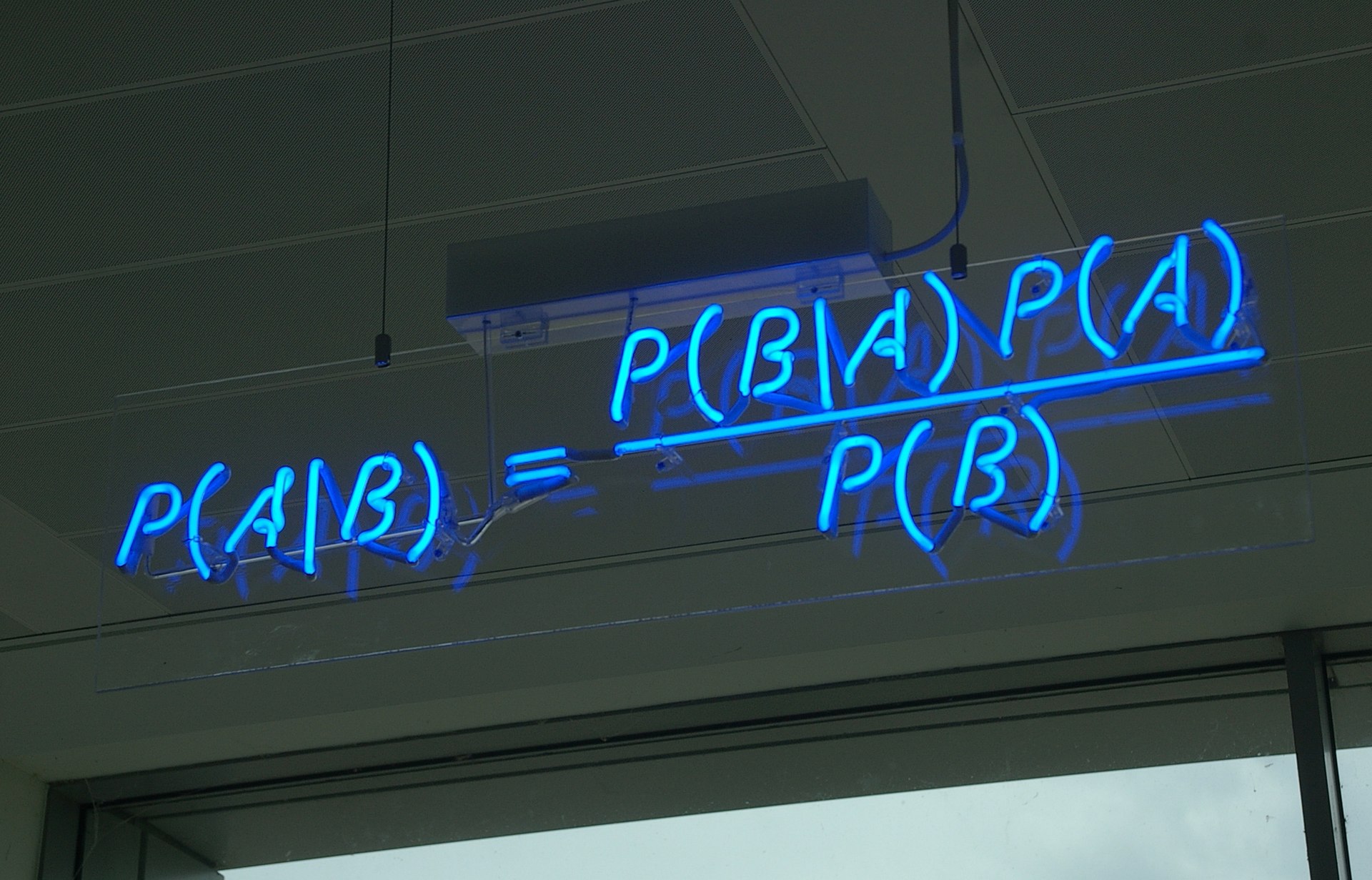



December 11th, 2023
式(5)右侧分子第一项少了条件概率x_0
不需要
请问为什么不需要呢,我看基本公式里面是需要的P(A/B,C)
它的假设就是$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1},\boldsymbol{x}_0)=p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$(马尔可夫链)
January 4th, 2024
苏神,我对“遗留问题”里面的讨论有一些疑问。之前公式(9)已经推出来了,只依靠Diffusion model forward process的假设($p(x_t|x_{t-1}), p(x_t|x_0), p(x_{t-1}|x_0)$都是正态分布),就能推导出来$p(x_{t-1}|x_{t},x_0)$的均值是$\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\boldsymbol{x}_0$,方差是一个固定的常数$\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}$。如果进一步将$x_0$建模为$x_t$的函数的话(我们通过$x_t$
来预测$x_0$),那么$p(x_{t-1}|{x_t})$的方差就应该也是$\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}$。但是为什么公式(16)和公式(18)推导出来在两个特殊case下,$p(x_{t-1}|{x_t})$的方差分别是$\beta_t^2$和$\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}$,不应该都是$\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}$吗?我的想法是,$p(x_{t-1}|{x_t})$的方差等于$\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}$是建立在两个假设之上的(或者说两个充分条件):(1)$p(x_t|x_{t-1}), p(x_t|x_0), p(x_{t-1}|x_0)$都是正态分布;(2)$x_0$可以被建模为$x_t$的函数。在Diffusion Model里,这两个假设都被使用了,因此在sampling时把$p(x_{t-1}|{x_t})$的方差设为$\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}$其实是比采用$\beta_t^2$作为方差更自洽的做法?请问苏神我的理解是对的吗?
你可以这样理解,给定$\boldsymbol{x}_t,\boldsymbol{x}_0$预测$\boldsymbol{x}_{t-1}$的方差是$\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}$没错,但事实上从$\boldsymbol{x}_t$预测$\boldsymbol{x}_0$也是不确定的,也是有方差的,所以从$\boldsymbol{x}_t$预测$\boldsymbol{x}_{t-1}$的方差实际上是它们俩的方差的组合,并不是单纯就等于$\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}$,所以DDPM用两个能精确计算的特例来提供最后的方差参考值也就能理解了。
更详细的讨论可以参考:https://kexue.fm/archives/9245
明白了,谢谢!我还想再追问一下:从道理上来说,用$\boldsymbol{x}_t$预测$\boldsymbol{x}_0$应该是一个不确定的过程;但是在Diffusion Model里,从$\boldsymbol{x}_t$预测$\boldsymbol{x}_0$被建模成了一个确定性的过程(一个UNet输入$\boldsymbol{x}_t$,输出是$\boldsymbol{x}_0$而不是$\boldsymbol{x}_0$的分布,所以我认为$\boldsymbol{x}_t$预测$\boldsymbol{x}_0$是一个确定性的过程,不知道这个理解有没有问题?)。如果$\boldsymbol{x}_t$预测$\boldsymbol{x}_0$是一个确定性的过程(也就是Diffusion Model的建模假设),那么$p(x_{t-1}|{x_t})$的方差是否就exactly的等于$\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2}$?
这里有一个误区,通过“某个模型 + 距离平方损失”直接进行重构$\boldsymbol{x}_0$,并不代表将$\boldsymbol{x}_t$预测$\boldsymbol{x}_0$建模为了一个确定性的过程,虽然你或者作者想象中是这样做的。
事实上,距离平方损失对应的是$-\log \mathcal{N}(\boldsymbol{x}_0;\boldsymbol{\mu}(\boldsymbol{x}_t),\sigma^2)$,这里的$\sigma$是某个常数。也就是说,距离平方损失其实只是将$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$建模为“方差为常数、均值为$\boldsymbol{\mu}(\boldsymbol{x}_t)$”的正态分布,并没有说方差为0。
而方差虽然假设为常数,但哪个常数最优还是未知的,所以才有 https://kexue.fm/archives/9245 的施展空间,该链接也是不需要重新训练模型的,也就是说直接用在DDPM训练好的模型上。所以说,DDPM或者其他扩散模型,并没有“将$\boldsymbol{x}_t$预测$\boldsymbol{x}_0$建模为了一个确定性的过程”。
January 8th, 2024
@苏剑林|comment-23484
感谢解答!我去仔细读下【生成扩散模型漫谈(七):最优扩散方差估计(上)】
April 18th, 2024
苏神您好,关于【预估修正】有一个问题想请教您一下。如果我们在推导$p(x_{t-1}|x_{t})$时不使用bayes,而是根据以下两个公式
$$ p(x_t|x_0) = \sqrt{\bar{a_t}}x_0 + \sqrt{1 - \bar{a_t}}\epsilon_{\theta} \\
p(x_{t-1}|x_0) = \sqrt{\bar{a_{t-1}}}x_0 + \sqrt{1 - \bar{a_{t-1}}}\epsilon $$
通过消去$x_0$,直接得到$x_{t-1}$关于$x_{t}$的表达式呢?其中$\epsilon_{\theta}$由$model(x_{t}, t)$给出,$\epsilon$则直接从$N(0, 1)$采样得到。以我浅薄的理解,这也是一种【预估修正】,即我们从$x_t$预估$\hat{x_0}$,并直接走到$\hat{x_0}$,但是因为$\hat{x_0}$并不准确,所以我们又退回来一些,到达$x_{t-1}$。
如果进一步推广,我们可以把任意的$t_1$和$t_2$赋值到前向公式$p(x_t|x_0)$的$t$中,再通过消去$x_0$得到任意2个时刻$t_1$与$t_2$间的转移方程(效果类似于DDIM,但是显然想法过于naive了)。
当然,我根据以上思路写代码试了一下,结果显示这个idea并不work。辗转反侧想不明白,所以来请教一下苏神,希望能得到一些指点
巧了,你这个处理方式,正好是 https://kexue.fm/archives/9262 一文中的公式(7)、(8)的模型,而它通常效果不好的原因在下面已经有分析。更好的做法应该是当这两个式子的噪声是同一个,然后联立消去噪声项,保留$\boldsymbol{x}_0$,然后用$\boldsymbol{x}_t$预测的$\boldsymbol{x}_0$替换掉$\boldsymbol{x}_0$项,这就得到了DDIM。
June 11th, 2024
苏神您好,我有一个问题。在DDPM的采样过程中,是从$x_T$开始一步步采样到最终的$x_0$,而$x_T$是从标准高斯分布中采样的,事实上每一步的$p(x_{t-1}|x_t)$我们是用$p(x_{t-1}|x_t, x_0 = \mu(x_t))$来近似的,而后者是个高斯分布,这会导致$T-1$时刻的分布也是高斯分布吗,这样经过$T$步采样会使得最终的$x_0$也是高斯分布吗?请问苏神我这样想的有什么问题吗?
$p(z)$是高斯分布,$p(x|z)$是条件高斯分布,不意味着$p(x)=\int p(x|z)p(z)dz$是高斯分布,事实上它甚至可以是任意复杂的分布。
比如GAN,它的理论基础也是上式,采样分布$p(z)$是标准正态分布,生成器则可以看成一个方差为0的条件高斯分布$p(x|z)$,但很显然,它可以生成很复杂的自然图像,而不单单是高斯噪声。
但是ddpm是高斯分布的叠加(减),理论上如果都是严格的高斯分布的话,却是只能得到高斯分布。GAN是把高斯分布放入一个函数,感觉不能这样简单的比较吧,或者说有区别但是不能这么简单的解释
跟GAN同理的,$p(\boldsymbol{x}_{t-2}|\boldsymbol{x}_{t-1})$、$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$都是高斯分布,不代表$p(\boldsymbol{x}_{t-2}|\boldsymbol{x}_t)$也是高斯分布。
June 13th, 2024
您好,公式(10)的标号没有显示
公式(13)的标号只显示了部分
用的是edge浏览器
Chrome和Safari测试正常,暂时无法测试所有浏览器,抱歉。
July 18th, 2024
\[
p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) \approx p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t),\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)
\]
"如果我们能够通过xt,来预测x0,那么不就可以消去p(xt−1|xt,x0)中的x0,使得它只依赖于xt了吗?"
这里能够近似约等于的理由 我觉得不够充分,希望博主能更具体展开说说吗
从直观上理解来说,左边的计算是不知道x0,所以理论上计算的时候需要对所有的x0做一个遍历然后积分计算,但实际上我们用神经网络预测一个最可能的x0,然后用它来近似计算。
同时,因为正态分布密度函数只有在靠近均值的时候才明显大于0,也就是说从直观意义上来说一个加噪图片只明显对应一个原图片,所以仅采用神经网络预测一个最可能的x0也有合理性。
我是这么理解。
甚至于可能训练出来的网络预测也不只是预测x0,他可能自动学习到的是预测多个可能x0的加权
首先,等式:
$$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) = \int p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0)p(\boldsymbol{x}_0|\boldsymbol{x}_t)d\boldsymbol{x}_0$$
是一个恒等式,它是联合分布和边缘分布的一个关系式。
我们本来要做的事情,是用正态分布去近似$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$,但非常巧合的是$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0)$也是正态分布,如果$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$也是正态分布的话,那么$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$也是正态分布。
也就是说,这个巧合,让我们可以将直接建模$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$,改为先建模$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$,然后间接得到$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$。只要$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$在努力用$\boldsymbol{x}_t$预测$\boldsymbol{x}_0$,那么间接得到的$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$也在努力用$\boldsymbol{x}_t$预测$\boldsymbol{x}_{t-1}$,这就是整个逻辑。
至于用$\boldsymbol{x}_t$能不能准确预测$\boldsymbol{x}_0$,其实不大重要,重点是“努力”,换句话说可以证明最大化$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$本质上等同于最大化$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$,“最大化”就行,也就是“努力”就行,不一定能精准。
August 7th, 2024
如果exp(二次函数)中的二次函数是类似于:(x-u)**2+7这种呢?还是正态分布吗?
话说为啥提问几次都不显示?
如果是开口向上的二次函数,那么exp(二次函数)根本无法归一化,所以连分布都不是,更不用说正态分布了。
你这个二次函数的问题不是出在后面$+7$,因为加一个常数无非是乘了一个$\text{e}^7$的常数,前面乘上一个$\frac{1}{\text{e}^7}$就抵消了。
关键在于$x^2$项的前面必须是负号,不然积分项是正无穷不收敛的
August 7th, 2024
请教下苏老师,前向过程既然已经定义好了:$\boldsymbol{x}_{t}=\alpha_{t} \boldsymbol{x}_{t-1}+\beta_{t} \varepsilon_{t}$,为什么不可以直接使用该公式由$\boldsymbol{x}_{t}$推导出$\boldsymbol{x}_{t-1}$呢
我不大确定你是不是想问为什么不直接建模$\boldsymbol{x}_t$预测$\boldsymbol{x}_{t-1}$的模型?如果是的话,可以参考 https://kexue.fm/archives/9119#%E9%99%8D%E4%BD%8E%E6%96%B9%E5%B7%AE
因为前向过程这个式子$x_t = \alpha_tx_{t-1} + \beta_t\epsilon{t}$虽然有个等号,但是他并不是个等式(equation),而是一个赋值操作。不能简单的按照等式的方法去移项求解$x_{t-1}=f(x_t)$。
原因就在于,$\epsilon_t$不是一个正常的变量,他是一个概率分布的采样,他是没有一个确定值的,每次采样都不一样,你把它移来移去他都不是同一个值。
等号的意思也不是左右相等,而是把右边的结果赋值给左边,他描述的是一个迭代过程。有点像编程语言里的等号,并不是代表左右相等。
赋值这个词很精准,受教了!
August 20th, 2024
苏老师您好,想请教一个问题,我看到有文献,用unet模型预测noise后,根据预测的noise和前向过程的公式变形,可以得到一个在第t步的预测x0,在训练的时候,对这个预测x0做一些约束,用作总体损失的一部分,我也尝试过这种方法,但是效果并不理想,是因为我的训练步不够多么,预估修正还没有达到一个理想的状态么?
抱歉啊,具体的理论推导我们可以交流一下,但涉及到实验中的效果优劣调试,我可能真就无能为力了,因为我自己的炼丹经验也不多。