生成扩散模型漫谈(二十七):将步长作为条件输入
By 苏剑林 | 2024-12-15 | 66625位读者 |这篇文章我们再次聚焦于扩散模型的采样加速。众所周知,扩散模型的采样加速主要有两种思路,一是开发更高效的求解器,二是事后蒸馏。然而,据笔者观察,除了上两篇文章介绍过的SiD外,这两种方案都鲜有能将生成步数降低到一步的结果。虽然SiD能做到单步生成,但它需要额外的蒸馏成本,并且蒸馏过程中用到了类似GAN的交替训练过程,总让人感觉差点意思。
本文要介绍的是《One Step Diffusion via Shortcut Models》,其突破性思想是将生成步长也作为扩散模型的条件输入,然后往训练目标中加入了一个直观的正则项,这样就能直接稳定训练出可以单步生成模型,可谓简单有效的经典之作。
ODE扩散 #
原论文的结论是基于ODE式扩散模型的,而对于ODE式扩散的理论基础,我们在本系列的(六)、(十二)、(十四)、(十五)、(十七)等博客中已经多次介绍,其中最简单的一种理解方式大概是(十七)中的ReFlow视角,下面我们简单重复一下。
假设$\boldsymbol{x}_0\sim p_0(\boldsymbol{x}_0)$是先验分布采样的随机噪声,$\boldsymbol{x}_1\sim p_1(\boldsymbol{x}_1)$是目标分布采样的真实样本(注:前面的文章中,普通都是$\boldsymbol{x}_T$是噪声、$\boldsymbol{x}_0$是目标样本,这里方便起见反过来了),ReFlow允许我们指定任意从$\boldsymbol{x}_0$到$\boldsymbol{x}_1$的运动轨迹,最简单的轨迹自然是直线:
\begin{equation}\boldsymbol{x}_t = (1-t)\boldsymbol{x}_0 + t \boldsymbol{x}_1\label{eq:line}\end{equation}
两边求导,就可以得到它满足的ODE(常微分方程):
\begin{equation}\frac{d\boldsymbol{x}_t}{dt} = \boldsymbol{x}_1 - \boldsymbol{x}_0\end{equation}
这个ODE很简单,但实际上没用,因为我们想要的是通过ODE由$\boldsymbol{x}_0$生成$\boldsymbol{x}_1$,而上述ODE却显式地依赖$\boldsymbol{x}_1$。为了解决这个问题,一个很简单的想法是“学一个$\boldsymbol{x}_t$的函数去逼近$\boldsymbol{x}_1 - \boldsymbol{x}_0$”,学完之后就用它来取代$\boldsymbol{x}_1 - \boldsymbol{x}_0$,即
\begin{equation}\boldsymbol{\theta}^* = \mathop{\text{argmin}}_{\boldsymbol{\theta}} \mathbb{E}_{\boldsymbol{x}_0\sim p_0(\boldsymbol{x}_0),\boldsymbol{x}_1\sim p_1(\boldsymbol{x}_1)}\left[\Vert\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - (\boldsymbol{x}_1 - \boldsymbol{x}_0)\Vert^2\right]\label{eq:loss}\end{equation}
以及
\begin{equation}\frac{d\boldsymbol{x}_t}{dt} = \boldsymbol{x}_1 - \boldsymbol{x}_0\quad\Rightarrow\quad\frac{d\boldsymbol{x}_t}{dt} = \boldsymbol{v}_{\boldsymbol{\theta}^*}(\boldsymbol{x}_t, t)\label{eq:ode-core}\end{equation}
这就是ReFlow。当然这里边还欠缺了一个理论证明,就是通过平方误差来拟合$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$所得到的ODE确实能生成我们期望的分布,这部分大家自行看《生成扩散模型漫谈(十七):构建ODE的一般步骤(下)》就好。
步长自洽 #
假设我们已经有了$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$,那么通过求解微分方程$\frac{d\boldsymbol{x}_t}{dt} = \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$就可以实现从$\boldsymbol{x}_0$到$\boldsymbol{x}_1$的变换。划重点,是“微分方程”,但实际上我们没法真的去数值计算微分方程,而是只能算“差分方程”:
\begin{equation}\boldsymbol{x}_{t + \epsilon} - \boldsymbol{x}_t = \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) \epsilon\label{eq:de}\end{equation}
这个差分方程是原始ODE的“欧拉近似”,近似程度取决于步长$\epsilon$的大小,当$\epsilon\to 0$时就精确等于原始ODE,换言之步长越小越精确。然而,生成步数等于$1/\epsilon$,我们希望生成步数越少越好,这意味着不能用太大的步长,最好$\epsilon$可以等于1,这样$\boldsymbol{x}_1 = \boldsymbol{x}_0 + \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_0, 0)$,一步就可以完成生成。
问题是,如果直接用大步长代入上式,最终所算得的$\boldsymbol{x}_1$必然会严重偏离精确解。这时候原论文(下称“Shortcut模型”)的巧妙构思就登场了:它认为模型$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$不应该只是$\boldsymbol{x}_t$和$t$的函数,还应该是步长$\epsilon$的函数,这样差分方程$\eqref{eq:de}$就可以自行适应步长:
\begin{equation}\boldsymbol{x}_{t + \epsilon} - \boldsymbol{x}_t = \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, \epsilon) \epsilon\end{equation}
目标$\eqref{eq:loss}$训练的是精确的ODE模型,所以它训练的是$\epsilon=0$的模型:
\begin{equation}\mathcal{L}_1 = \mathbb{E}_{\boldsymbol{x}_0\sim p_0(\boldsymbol{x}_0),\boldsymbol{x}_1\sim p_1(\boldsymbol{x}_1)}\left[\frac{1}{2}\Vert\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, 0) - (\boldsymbol{x}_1 - \boldsymbol{x}_0)\Vert^2\right]\end{equation}
那$\epsilon > 0$的部分又怎么训练呢?我们的目标是生成步数越少越好,这等价于说希望“两倍的步长走1步等于单倍的步长走2步”:
\begin{equation}\boldsymbol{x}_t + \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, 2\epsilon) 2\epsilon = \color{green}{\underbrace{\boldsymbol{x}_t + \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, \epsilon) \epsilon}_{\tilde{\boldsymbol{x}}_{t+\epsilon}}} + \boldsymbol{v}_{\boldsymbol{\theta}}\big(\color{green}{\underbrace{\boldsymbol{x}_t + \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, \epsilon) \epsilon}_{\tilde{\boldsymbol{x}}_{t+\epsilon}}}, t+\epsilon, \epsilon\big) \epsilon\label{eq:cond}\end{equation}
即$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, 2\epsilon) = [\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, \epsilon) + \boldsymbol{v}_{\boldsymbol{\theta}}(\color{green}{\tilde{\boldsymbol{x}}_{t+\epsilon}}, t+\epsilon, \epsilon)] /2$。为了达到这个目标,我们补充一项自洽性损失函数
\begin{equation}\mathcal{L}_2 = \mathbb{E}_{\boldsymbol{x}_0\sim p_0(\boldsymbol{x}_0),\boldsymbol{x}_1\sim p_1(\boldsymbol{x}_1)}\left[\Vert\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, 2\epsilon) - [\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, \epsilon)+ \boldsymbol{v}_{\boldsymbol{\theta}}(\color{green}{\tilde{\boldsymbol{x}}_{t+\epsilon}}, t+\epsilon, \epsilon) ]/2\Vert^2\right]\end{equation}
$\mathcal{L}_1$与$\mathcal{L}_2$相加,就构成了Shortcut模型的损失函数。
(注:有读者指出,更早的《Consistency Trajectory Models: Learning Probability Flow ODE Trajectory of Diffusion》提出过以离散化时间的起点和终点作为条件输入的做法,指定起点和终点后步长其实也就确定了,所以Shortcut以步长为输入的做法并不算完全创新。)
模型细节 #
以上基本就是Shortcut模型的全部理论内容,非常精巧且简明,但从理论到实验,还需要一些细节,比如步长$\epsilon$如何融入到模型中去。
首先,在训练$\mathcal{L}_2$时,Shortcut并没有均匀地从$[0,1]$采样$\epsilon$,而是设置了一个最小步长$2^{-7}$,然后将它们倍增至1,即所有的非零步长只有$\{2^{-7},2^{-6},2^{-5},2^{-4},2^{-3},2^{-2},2^{-1},1\}$这8个值,从前7个中均匀采样来训练$\mathcal{L}_2$。这样一来,$\epsilon$的取值就是有限的,算上$0$一共就只有9个,所以Shortcut模型直接以Embedding的方式来输入$\epsilon$,将它跟$t$的Embedding加在一起。
其次,注意到$\mathcal{L}_2$的计算量是比$\mathcal{L}_1$大的,因为$\boldsymbol{v}_{\boldsymbol{\theta}}(\tilde{\boldsymbol{x}}_{t+\epsilon}, t, \epsilon)$这一项需要两次前向传播,所以论文的做法是每个batch中$3/4$的样本都用来计算$\mathcal{L}_1$,剩下的$1/4$样本才用来算$\mathcal{L}_2$。该操作不仅是为了节省计算量,实际上还调节了$\mathcal{L}_1,\mathcal{L}_2$的权重,因为$\mathcal{L}_2$比$\mathcal{L}_1$更好训练,所以它的训练样本可以适当少些。
除此之外,论文在实践的时候还对$\mathcal{L}_2$做了微调,多加了个stop gradient算子:
\begin{equation}\mathcal{L}_2 = \mathbb{E}_{\boldsymbol{x}_0\sim p_0(\boldsymbol{x}_0),\boldsymbol{x}_1\sim p_1(\boldsymbol{x}_1)}\left[\Vert\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, 2\epsilon) - \color{skyblue}{\text{sg}[}\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t, \epsilon)+ \boldsymbol{v}_{\boldsymbol{\theta}}(\color{green}{\tilde{\boldsymbol{x}}_{t+\epsilon}}, t+\epsilon, \epsilon) \color{skyblue}{]}/2\Vert^2\right]\end{equation}
为什么要这样做呢?按照作者的回复,这是自引导学习的常见做法,被stop gradient的部分属于目标,不应该有梯度,跟BYOL、SimSiam等无监督学习方案类似。不过照笔者看来,这个操作最大的价值还是节省训练成本,因为$\boldsymbol{v}_{\boldsymbol{\theta}}(\tilde{\boldsymbol{x}}_{t+\epsilon}, t, \epsilon)$这一项做了两次前向传播,如果要对它反向传播,计算量也要翻倍。
实验效果 #
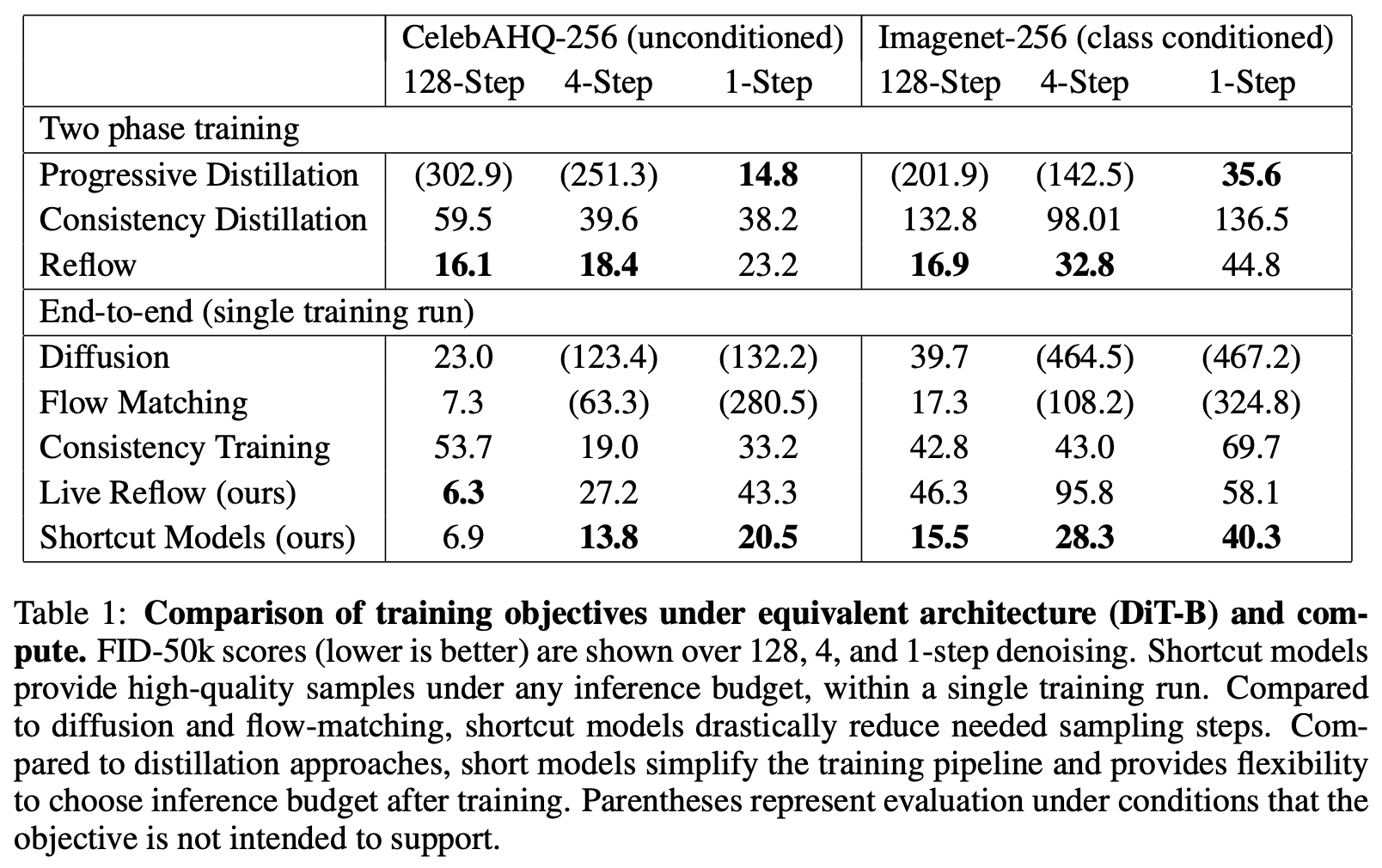
现在我们来看Shortcut模型的实验效果,看起来它是目前单步生成效果最好的、单阶段训练的扩散模型:
这是它的实际采样效果图:
不过仔细观察单步生成的样本就会发现,其实还有明显的瑕疵,所以说虽然Shortcut模型相比于之前的单阶段训练方案来说已经取得了较大的进步,但还有明显的提升空间。
作者已经将Shortcut模型的代码开源,Github链接是:
顺便说,Shortcut模型投到了ICLR 2025上,获得了reviewer的一致好评(全8分)。
延伸思考 #
看到Shortcut模型,不知道大家想到了哪些相关工作?笔者想到了一个可能大家都意想不到的,那就是我们在《生成扩散模型漫谈(二十一):中值定理加速ODE采样》介绍过的AMED。
Shortcut模型与AMED的底层思想是相通的,它们都已经发现,单靠研究复杂的高阶求解器,将生成的NFE(模型的运行次数)降低到个位数就已经很简单了,更不用说做单步生成了。所以它们一致认为,真正要变的并不是求解器,而是模型。该怎么变呢?AMED想到的是“中值定理”:对ODE两端积分,我们有精确的
\begin{equation}\boldsymbol{x}_{t + \epsilon} - \boldsymbol{x}_t = \int_t^{t + \epsilon}\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{\tau}, \tau) d\tau\end{equation}
类比“积分中值定理”,我们能找到一个$s\in[t, t + \epsilon]$,成立
\begin{equation}\frac{1}{\epsilon}\int_t^{t + \epsilon}\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_{\tau}, \tau) d\tau = \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_s, s)\end{equation}
于是我们得到
\begin{equation}\boldsymbol{x}_{t + \epsilon} - \boldsymbol{x}_t = \boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_s, s) \epsilon\end{equation}
当然,积分中值定理实际上只对标量函数成立,对向量函数是不保证成立的,所以说是“类比”。现在的问题是并不知道$s$的值,所以AMED的后续做法是用一个非常小的(计算量几乎可以忽略的)模型去预测$s$。
AMED是基于现成扩散模型的事后修正方法,因此它的效果取决于中值定理对$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$模型的成立程度,这显得有些“运气成分”,并且AMED需要先用欧拉格式预估一下$\boldsymbol{x}_s$,所以它的NFE最少是2,不能做到单步生成。相比之下,Shortcut模型更“激进”,它直接把步长作为条件输入,将加速生成的条件$\eqref{eq:cond}$作为损失函数,这样一来不仅避免了“中值定理”近似的可行性讨论,还使得最少NFE可以降低到1。
更巧妙的是,细思之下我们会发现两者的做法其实也有些共性,前面我们说了Shortcut是直接将$\epsilon$转成Embedding加到$t$的Embeddding上的,这不相当于跟AMED一样都是修改$t$嘛!只不过AMED是直接修改$t$的数值,而Shortcut修改的是$t$的Embedding。
文章小结 #
本文介绍了一个单阶段训练就可以实现单步生成的扩散模型新工作,它的突破思想是将步长也当成条件输入到扩散模型中,并配以一个直观的正则项,这样只通过单阶段训练就可以得到单步生成的扩散模型。
转载到请包括本文地址:https://kexue.fm/archives/10617
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Dec. 15, 2024). 《生成扩散模型漫谈(二十七):将步长作为条件输入 》[Blog post]. Retrieved from https://kexue.fm/archives/10617
@online{kexuefm-10617,
title={生成扩散模型漫谈(二十七):将步长作为条件输入},
author={苏剑林},
year={2024},
month={Dec},
url={\url{https://kexue.fm/archives/10617}},
}











December 15th, 2024
您好,请问(8)式右边第三项中,$v_\theta$的输入为什么是$t$而不是$t+\epsilon$呀?原文也是$t$,感到疑惑。
另:(8)式左边第二项$v_\theta$的输入应该是$2\epsilon$。
谢谢。
左边的笔误已修正,右端我也同意用$t+\epsilon$更合理,按照这个方式来写了。谢谢指出。
December 18th, 2024
看了原文,似乎也可以理解为一种一边训练diffusion一边distill的过程
$v_\theta(x_t, t,0)$的训练就是原本的diffusion,$v_\theta(x_t, t,d)$在训练过程中不断地吸收$d=0$的trajectories
$v_\theta(x_t, t,d)$的训练也完全不影响$v_\theta(x_t, t,0)$
如果用另一个网络$u$来做非零步长$d$也似乎可行,比如$u_\theta(x_t, t,d)$,说不定$u$还可以再简化
可以这么理解。
但用另一个模型来做$v_\theta(x_t, t,d)$简化不了吧?除非预测$v_\theta(x_t, t,d)$与$v_\theta(x_t, t,0)$的残差,可能还有机会。
December 19th, 2024
感觉有些像Progressive Distillation,相当于在finetune teacher model
是的,同感,我感觉 training cost 层面想要得到一个 one-step sampling 的扩散模型,是没有 free lunch 的。shortcut 模型学完,像是集成了 progressive distialltion 的多个学生模型
问题来了,如果是one-step sampling还能不能叫扩散模型呢
December 30th, 2024
感觉和这篇很像Catch-Up Distillation: You Only Need to Train Once for Accelerating Sampling然而这篇没中哈哈。不知道和ECT这种改进的CT比怎么样,之前实验跑过类似的,前传的成本其实也是有一些的。
Catch-Up Distillation相对来说还是复杂一些。ECT大致上相当于CT的EMA衰减系数设为0?我对CT这套方案其实兴趣不大,没有试验过,所以也不好判断优劣。当然本文的模型也未必是SOTA,只是学习到了“步长作为条件输入”这个思想,跟大家分享一下。
ECT 和CT分别是哪两片?
CT是https://arxiv.org/abs/2303.01469;ECT是https://arxiv.org/abs/2406.14548
February 8th, 2025
shortcut这类直接end-to-end的工作是不是暂时还比不过SiD这类后处理蒸馏
暂时是的
如果网络的预测目标不是速度而是x0的话(对应地不能用简单的一阶Euler采样了),这个时候在速度上约束这样的一致性还有用吗?
还是说在x0空间也可以推出相似的结论呢
预测速度跟预测$\boldsymbol{x}_0$本质上是等价的呀,而且最终生成过程也是一个ODE吧?
April 10th, 2025
感觉Shortcut Models可以看作基于Flow-Macting的CMs?
翻了翻我对一致性模型的理解( https://kexue.fm/archives/10633 ),好像没法对得上。
May 7th, 2025
(9)中如果忽略步长条件的作用,是不是就跟CM的损失函数等价了。这样看的话,步长嵌入的作用存疑
May 23rd, 2025
苏神可以看看最近的《Mean Flows for One-step Generative Modeling》吗?从Flow Mathcing角度做One Step的,看起来效果比ShortCut好多了。
https://kexue.fm/archives/10958 新鲜出炉
July 3rd, 2025
请问ϵ为什么要限制到2^-7, 2^-6, .. 2^-1, 2^0这8个数,感觉没有必要
从shortcut的整篇文风和结果来看,作者的原则是“够用即可”,所以步长假设这8个数确实很符合这个风格。
August 27th, 2025
从模型角度来说model(xt,t,d)和meanflow的model(xt,t1,t2)是等价的对吧
从理论能力来说是等价的,不过实践表现可能会有差距。