Muon优化器赏析：向量与矩阵有何本质区别？

随着LLM时代的到来，学术界对于优化器的研究热情似乎有所减退。这主要是因为目前主流的AdamW已经能够满足大多数需求，而如果对优化器“大动干戈”，那么需要巨大的验证成本。因此，当前优化器的变化，多数都只是工业界根据自己的训练经验来对AdamW打的一些小补丁。

不过，最近推特上一个名为“Muon”的优化器颇为热闹，它声称比AdamW更为高效，且并不只是在Adam基础上的“小打小闹”，而是体现了关于向量与矩阵差异的一些值得深思的原理。本文让我们一起赏析一番。

算法初探 #

Muon全称是“MomentUm Orthogonalized by Newton-schulz”，它适用于矩阵参数$\boldsymbol{W}\in\mathbb{R}^{n\times m}$，其更新规则是
\begin{equation}\begin{aligned}
\boldsymbol{M}_t =&\, \beta\boldsymbol{M}_{t-1} + \boldsymbol{G}_t \\[5pt]
\boldsymbol{W}_t =&\, \boldsymbol{W}_{t-1} - \eta_t [\text{msign}(\boldsymbol{M}_t) + \lambda \boldsymbol{W}_{t-1}] \\
\end{aligned}\end{equation}
这里$\text{msign}$是矩阵符号函数，它并不是简单地对矩阵每个分量取$\text{sign}$操作，而是$\text{sign}$函数的矩阵化推广，它跟SVD的关系是：
\begin{equation}\boldsymbol{U},\boldsymbol{\Sigma},\boldsymbol{V}^{\top} = SVD(\boldsymbol{M}) \quad\Rightarrow\quad \text{msign}(\boldsymbol{M}) = \boldsymbol{U}_{[:,:r]}\boldsymbol{V}_{[:,:r]}^{\top}\end{equation}
其中$\boldsymbol{U}\in\mathbb{R}^{n\times n},\boldsymbol{\Sigma}\in\mathbb{R}^{n\times r},\boldsymbol{V}\in\mathbb{R}^{m\times m}$，$r$是$\boldsymbol{M}$的秩。更多的理论细节我们稍后再展开，这里我们先来尝试直观感知如下事实：

Muon是一个类似于Adam的自适应学习率优化器。

像Adagrad、RMSprop、Adam等自适应学习率优化器的特点是通过除以梯度平方的滑动平均的平方根来调整每个参数的更新量，这达到了两个效果：1、损失函数的常数缩放不影响优化轨迹；2、每个参数分量的更新幅度尽可能一致。Muon正好满足这两个特性：

1、损失函数乘以$\lambda$，$\boldsymbol{M}$也会乘以$\lambda$，结果是$\boldsymbol{\Sigma}$被乘以$\lambda$，但Muon最后的更新量是将$\boldsymbol{\Sigma}$变为单位阵，所以不影响优化结果；

2、当$\boldsymbol{M}$被SVD为$\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^{\top}$时，$\boldsymbol{\Sigma}$的不同奇异值体现了$\boldsymbol{M}$的“各向异性”，而将它们都置一则更加各向同性，也起到同步更新幅度的作用。

（注：Muon还有个Nesterov版，它只是将更新规则中的$\text{msign}(\boldsymbol{M}_t)$换成$\text{msign}(\beta\boldsymbol{M}_t + \boldsymbol{G}_t)$，其余部份完全一致，简单起见就不在正文中展开介绍了。）

符号函数 #

利用SVD，我们还可以证明恒等式
\begin{equation}\text{msign}(\boldsymbol{M}) = (\boldsymbol{M}\boldsymbol{M}^{\top})^{-1/2}\boldsymbol{M}= \boldsymbol{M}(\boldsymbol{M}^{\top}\boldsymbol{M})^{-1/2}\label{eq:msign-id}\end{equation}
其中${}^{-1/2}$是矩阵的$1/2$次幂的逆矩阵，如果不可逆的话则取伪逆。这个恒等式能让我们更好理解为什么$\text{msign}$是$\text{sign}$的矩阵推广：对于标量$x$我们有$\text{sign}(x)=x(x^2)^{-1/2}$，正是上式的一个特殊情形（当$\boldsymbol{M}$是$1\times 1$矩阵时）。这个特殊例子还可以推广到对角阵$\boldsymbol{M}=\text{diag}(\boldsymbol{m})$：
\begin{equation}\text{msign}(\boldsymbol{M}) = \text{diag}(\boldsymbol{m})[\text{diag}(\boldsymbol{m})^2]^{-1/2} = \text{diag}(\text{sign}(\boldsymbol{m}))=\text{sign}(\boldsymbol{M})\end{equation}
其中$\text{sign}(\boldsymbol{m})$、$\text{sign}(\boldsymbol{M})$是指向量/矩阵的每个分量都取$\text{sign}$。上式意味着，当$\boldsymbol{M}$是对角阵时，Muon就退化为带动量的SignSGD（Signum）或笔者所提的Tiger，它们都是Adam的经典近似。反过来说，Muon与Signum、Tiger的区别就是Element-wise的$\text{sign}(\boldsymbol{M})$替换成了矩阵版$\text{msign}(\boldsymbol{M})$。

对于$n$维向量来说，我们还可以视为$n\times 1$的矩阵，此时$\text{msign}(\boldsymbol{m}) = \boldsymbol{m}/\Vert\boldsymbol{m}\Vert_2$正好是$l_2$归一化。所以，在Muon框架下对向量我们有两种视角：一是对角矩阵，如LayerNorm的gamma参数，结果是对动量取$\text{sign}$；二是$n\times 1$的矩阵，结果是对动量做$l_2$归一化。此外，输入和输出的Embedding虽然也是矩阵，但它们使用上是稀疏的，所以更合理的方式也是将它们当成多个向量独立处理。

当$m=n=r$时，$\text{msign}(\boldsymbol{M})$还有一个意义是“最优正交近似”：
\begin{equation}\text{msign}(\boldsymbol{M}) = \mathop{\text{argmin}}_{\boldsymbol{O}^{\top}\boldsymbol{O} = \boldsymbol{I}}\Vert \boldsymbol{M} - \boldsymbol{O}\Vert_F^2 \label{eq:nearest-orth}\end{equation}
类似地，对于$\text{sign}(\boldsymbol{M})$我们可以写出（假设$\boldsymbol{M}$没有零元素）：
\begin{equation}\text{sign}(\boldsymbol{M}) = \mathop{\text{argmin}}_{\boldsymbol{O}\in\{-1,1\}^{n\times m}}\Vert \boldsymbol{M} - \boldsymbol{O}\Vert_F^2\end{equation}
不论是$\boldsymbol{O}^{\top}\boldsymbol{O} = \boldsymbol{I}$还是$\boldsymbol{O}\in\{-1,1\}^{n\times m}$，我们都可以视为对更新量的一种规整化约束，所以Muon和Signum、Tiger可以视作是同一思路下的优化器，它们都以动量$\boldsymbol{M}$为出发点来构建更新量，只是为更新量选择了不同的规整化方法。

式$\eqref{eq:nearest-orth}$的证明：对于正交矩阵$\boldsymbol{O}$，我们有
\begin{equation}\begin{aligned}
\Vert \boldsymbol{M} - \boldsymbol{O}\Vert_F^2 =&\, \Vert \boldsymbol{M}\Vert_F^2 + \Vert \boldsymbol{O}\Vert_F^2 - 2\langle\boldsymbol{M},\boldsymbol{O}\rangle_F \\[5pt]
=&\, \Vert \boldsymbol{M}\Vert_F^2 + n - 2\text{Tr}(\boldsymbol{M}\boldsymbol{O}^{\top})\\[5pt]
=&\, \Vert \boldsymbol{M}\Vert_F^2 + n - 2\text{Tr}(\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^{\top}\boldsymbol{O}^{\top})\\[5pt]
=&\, \Vert \boldsymbol{M}\Vert_F^2 + n - 2\text{Tr}(\boldsymbol{\Sigma}\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U})\\
=&\, \Vert \boldsymbol{M}\Vert_F^2 + n - 2\sum_{i=1}^n \boldsymbol{\Sigma}_{i,i}(\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U})_{i,i}
\end{aligned}\end{equation}
其中涉及到的运算规则我们在伪逆中已经介绍过。由于$\boldsymbol{U},\boldsymbol{V},\boldsymbol{O}$都是正交矩阵，所以$\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U}$也是正交矩阵，正交矩阵的每个分量必然不超过1，又因为$\boldsymbol{\Sigma}_{i,i} > 0$，所以上式取最小值对应于每个$(\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U})_{i,i}$取最大值，即$(\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U})_{i,i}=1$，这意味着$\boldsymbol{V}^{\top}\boldsymbol{O}^{\top}\boldsymbol{U}=\boldsymbol{I}$，即$\boldsymbol{O}=\boldsymbol{U}\boldsymbol{V}^{\top}$。

该结论还可以仔细地推广到$m,n,r$不相等的情形，但这里不作进一步展开。

迭代求解 #

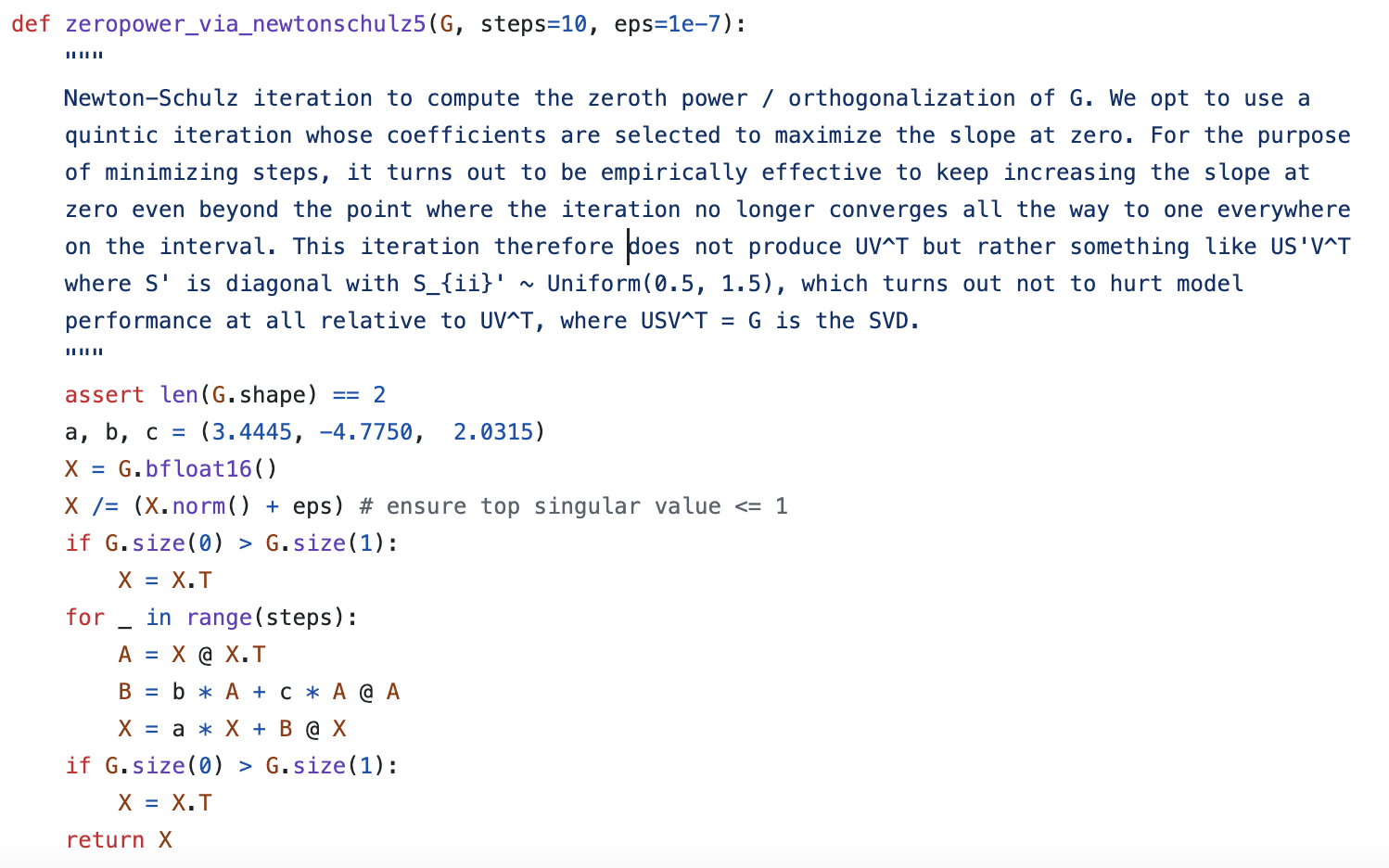
实践中，如果每一步都对$\boldsymbol{M}$做SVD来求解$\text{msign}(\boldsymbol{M})$的话，那么计算成本还是比较大的，因此作者提出了用Newton-schulz迭代来近似计算$\text{msign}(\boldsymbol{M})$。

迭代的出发点是恒等式$\eqref{eq:msign-id}$，不失一般性，我们假设$n\geq m$，然后考虑在$\boldsymbol{M}^{\top}\boldsymbol{M}=\boldsymbol{I}$处泰勒展开$(\boldsymbol{M}^{\top}\boldsymbol{M})^{-1/2}$，展开的方式是直接将标量函数$t^{-1/2}$的结果用到矩阵中：
\begin{equation}t^{-1/2} = 1 - \frac{1}{2}(t-1) + \frac{3}{8}(t-1)^2 - \frac{5}{16}(t-1)^3 + \cdots\end{equation}
保留到二阶，结果是$(15 - 10t + 3t^2)/8$，那么我们有
\begin{equation}\text{msign}(\boldsymbol{M}) = \boldsymbol{M}(\boldsymbol{M}^{\top}\boldsymbol{M})^{-1/2}\approx \frac{15}{8}\boldsymbol{M} - \frac{5}{4}\boldsymbol{M}(\boldsymbol{M}^{\top}\boldsymbol{M}) + \frac{3}{8}\boldsymbol{M}(\boldsymbol{M}^{\top}\boldsymbol{M})^2\end{equation}
假如$\boldsymbol{X}_t$是$\text{msign}(\boldsymbol{M})$的某个近似，我们认为将它代入上式后，会得到$\text{msign}(\boldsymbol{M})$的一个更好的近似，于是我们得到一个可用的迭代格式
\begin{equation}\boldsymbol{X}_{t+1} = \frac{15}{8}\boldsymbol{X}_t - \frac{5}{4}\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t) + \frac{3}{8}\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t)^2\end{equation}
然而，查看Muon的官方代码我们就会发现，它里边的Newton-schulz迭代确实是这个形式，但三个系数却是$(3.4445, -4.7750, 2.0315)$，而且作者没有给出数学推导，只有一段语焉不详的注释：

收敛加速 #

为了猜测官方迭代算法的来源，我们考虑一般的迭代过程
\begin{equation}\boldsymbol{X}_{t+1} = a\boldsymbol{X}_t + b\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t) + c\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t)^2\label{eq:iteration}\end{equation}
其中$a,b,c$是三个待求解的系数，如果想要更高阶的迭代算法，我们也可以逐次补充$\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t)^3$、$\boldsymbol{X}_t(\boldsymbol{X}_t^{\top}\boldsymbol{X}_t)^4$等项，下面的分析过程是通用的。

我们选择的初始值是$\boldsymbol{X}_0=\boldsymbol{M}/\Vert\boldsymbol{M}\Vert_F$，$\Vert\Vert_F$是矩阵的范数，选择的依据是除以$\Vert\boldsymbol{M}\Vert_F$不改变SVD的$\boldsymbol{U},\boldsymbol{V}$，但可以让$\boldsymbol{X}_0$的所有奇异值都在$[0,1]$之间，让迭代的初始奇异值更标准一些。现在假设$\boldsymbol{X}_t$可以SVD为$\boldsymbol{U}\boldsymbol{\Sigma}_t\boldsymbol{V}^{\top}$，那么代入上式我们可以得到
\begin{equation}\boldsymbol{X}_{t+1} = \boldsymbol{U}_{[:,:r]}(a \boldsymbol{\Sigma}_{t,[:r,:r]} + b \boldsymbol{\Sigma}_{t,[:r,:r]}^3 + c \boldsymbol{\Sigma}_{t,[:r,:r]}^5)\boldsymbol{V}_{[:,:r]}^{\top}\end{equation}
因此，式$\eqref{eq:iteration}$实际上在迭代奇异值组成的对角阵$\boldsymbol{\Sigma}_{[:r,:r]}$，如果记$\boldsymbol{X}_t=\boldsymbol{U}_{[:,:r]}\boldsymbol{\Sigma}_{t,[:r,:r]}\boldsymbol{V}_{[:,:r]}^{\top}$，那么有$\boldsymbol{\Sigma}_{t+1,[:r,:r]} = g(\boldsymbol{\Sigma}_{t,[:r,:r]})$，其中$g(x) = ax + bx^3 + cx^5$。又因为对角阵的幂等于对角线元素各自取幂，所以问题简化成单个奇异值$\sigma$的迭代。我们的目标是计算$\boldsymbol{U}_{[:,:r]}\boldsymbol{V}_{[:,:r]}^{\top}$，换言之希望通过迭代将$\boldsymbol{\Sigma}_{[:r,:r]}$变为单位阵，这又可以简化为迭代$\sigma_{t+1} = g(\sigma_t)$将单个奇异值变为1。

受@leloykun启发，我们将$a,b,c$的选择视为一个最优化问题，目标是让迭代过程对于任意初始奇异值都收敛得尽可能快。首先我们将$g(x)$重新参数化为
\begin{equation}g(x) = x + \kappa x(x^2 - x_1^2)(x^2 - x_2^2)\end{equation}
其中$x_1 \leq x_2$。该参数化的好处是直观表示出了迭代的5个不动点$0,\pm x_1,\pm x_2$。由于我们的目标是收敛到1，因此初始化我们选择$x_1 < 1,x_2 > 1$，想法是不管迭代过程往$x_1$走还是往$x_2$走，结果都是1附近。

接下来，我们确定迭代步数$T$，这样迭代过程就称为一个确定性函数，然后我们将矩阵的形状（即$n,m$）确定好，就可以采样一批矩阵，并通过SVD来算奇异值。最后，我们将这些奇异值当成输入，而目标输出则是1，损失函数是平方误差，整个模型完全可导，可以用梯度下降解决（@leloykun则假设了$x_1 + x_2 = 2$，然后用网格搜索来求解）。

一些计算结果：
\begin{array}{ccc|ccc|ccc|c}
\hline
n & m & T & \kappa & x_1 & x_2 & a & b & c & \text{mse}\\
\hline
1024 & 1024 & 3 & 7.020 & 0.830 & 0.830 & 4.328 & -9.666 & 7.020 & 0.10257 \\
1024 & 1024 & 5 & 1.724 & 0.935 & 1.235 & 3.297 & -4.136 & 1.724 & 0.02733 \\
2048 & 1024 & 3 & 7.028 & 0.815 & 0.815 & 4.095 & -9.327 & 7.028 & 0.01628 \\
2048 & 1024 & 5 & 1.476 & 0.983 & 1.074 & 2.644 & -3.128 & 1.476 & 0.00038 \\
4096 & 1024 & 3 & 6.948 & 0.802 & 0.804 & 3.886 & -8.956 & 6.948 & 0.00371 \\
4096 & 1024 & 5 & 1.214 & 1.047 & 1.048 & 2.461 & -2.663 & 1.214 & 0.00008 \\
\hline
2048 & 2048 & 3 & 11.130 & 0.767 & 0.767 & 4.857 & -13.103 & 11.130 & 0.10739 \\
2048 & 2048 & 5 & 1.779 & 0.921 & 1.243 & 3.333 & -4.259 & 1.779 & 0.03516 \\
4096 & 4096 & 3 & 18.017 & 0.705 & 0.705 & 5.460 & -17.929 & 18.017 & 0.11303 \\
4096 & 4096 & 5 & 2.057 & 0.894 & 1.201 & 3.373 & -4.613 & 2.057 & 0.04700 \\
8192 & 8192 & 3 & 30.147 & 0.643 & 0.643 & 6.139 & -24.893 & 30.147 & 0.11944 \\
8192 & 8192 & 5 & 2.310 & 0.871 & 1.168 & 3.389 & -4.902 & 2.310 & 0.05869 \\
\hline
\end{array}

从表格可以看出，结果跟矩阵大小、迭代步数都有明显关系；从损失函数来看，非方阵比方阵更容易收敛；Muon作者给出的$a,b,c$，大概是迭代步数为5时方阵的最优解。当迭代步数给定时，结果依赖于矩阵大小，这本质上是依赖于奇异值的分布，关于这个分布有个值得一提的结果是当$n,m\to\infty$时为Marchenko–Pastur分布。

参考代码：

import jax
import jax.numpy as jnp
from tqdm import tqdm

n, m, T = 1024, 1024, 5
key, data = jax.random.key(42), jnp.array([])
for _ in tqdm(range(1000), ncols=0, desc='SVD'):
    key, subkey = jax.random.split(key)
    M = jax.random.normal(subkey, shape=(n, m))
    S = jnp.linalg.svd(M, full_matrices=False)[1]
    data = jnp.concatenate([data, S / (S**2).sum()**0.5])

@jax.jit
def f(w, x):
    k, x1, x2 = w
    for _ in range(T):
        x = x + k * x * (x**2 - x1**2) * (x**2 - x2**2)
    return ((x - 1)**2).mean()

f_grad = jax.grad(f)
w, u = jnp.array([1, 0.9, 1.1]), jnp.zeros(3)
for _ in tqdm(range(100000), ncols=0, desc='SGD'):
    u = 0.9 * u + f_grad(w, data)  # 动量加速
    w = w - 0.01 * u

k, x1, x2 = w
a, b, c = 1 + k * x1**2 * x2**2, -k * (x1**2 + x2**2), k
print(f'{n} & {m} & {T} & {k:.3f} & {x1:.3f} & {x2:.3f} & {a:.3f} & {b:.3f} & {c:.3f} & {f(w, data):.5f}')

一些思考 #

如果按照默认选择$T=5$，那么对于一个$n\times n$的矩阵参数，Muon的每一步更新至少需要算15次$n\times n$与$n\times n$的矩阵乘法，这计算量毋庸置疑是比Adam明显大的，由此可能有读者担心Muon实践上是否可行。

事实上，这种担心是多余的，Muon计算虽然比Adam复杂，但每一步增加的时间不多，笔者的结论是5%内，Muon作者则声称能做到2%。这是因为Muon的矩阵乘法发生在当前梯度计算完后、下一梯度计算前，这期间几乎所有的算力都是空闲的，而这些矩阵乘法是静态大小且可以并行，因此不会明显增加时间成本，反而是Muon比Adam少一组缓存变量，显存成本更低。

Muon最值得深思的地方，其实是向量与矩阵的内在区别，以及它对优化的影响。SGD、Adam、Tiger等常见优化器的更新规则是Element-wise的，即不论向量、矩阵参数，实际都视为一个大向量，分量按照相同的规则独立地更新。具备这个特性的优化器往往理论分析起来更加简化，也方便张量并行，因为一个大矩阵切成两个小矩阵独立处理，并不改变优化轨迹。

但Muon不一样，它以矩阵为基本单位，考虑了矩阵的一些独有特性。可能有些读者会奇怪：矩阵和向量不都只是一堆数字的排列吗，能有什么区别？举个例子，矩阵我们有“迹（trace）”这个概念，它是对角线元素之和，这个概念不是瞎定义的，它有一个重要特性是在相似变换下保持不变，它还等于矩阵的所有特征值之和。从这个例子就可以看出，矩阵的对角线元素跟非对角线元素，地位其实是不完全对等的。而Muon正是因为考虑了这种不对等性，才有着更好的效果。

当然，这也会导致一些负面影响。如果一个矩阵被划分到不同设备上，那么用Muon时就需要将它们的梯度就需要汇聚起来再计算更新量了，而不能每个设备独立更新，这增加了通信成本。即便我们不考虑并行方面，这个问题也存在，比如Multi-Head Attention一般是通过单个大矩阵投影到$Q$（$K,V$同理），然后用reshape的方式得到多个Head，这样在模型参数中就只有单个矩阵，但它本质上是多个小矩阵，所以按道理我们需要将大矩阵拆开成多个小矩阵独立更新。

总之，Muon这种非Element-wise的更新规则，在捕捉向量与矩阵的本质差异的同时，也会引入一些小问题，这可能会不满足一些读者的审美。

（补充：几乎在本博客发布的同时，Muon的作者Keller Jordan也发布了自己的一篇博客《Muon: An optimizer for hidden layers in neural networks》。）

范数视角 #

从理论上看，Muon捕捉了矩阵的什么关键特性呢？也许接下来的范数视角可以回答我们的问题。

这一节的讨论主要参考了论文《Stochastic Spectral Descent for Discrete Graphical Models》和《Old Optimizer, New Norm: An Anthology》，特别是后一篇。不过其中的出发点并不是新的，我们在《梯度流：探索通向最小值之路》就已经简单涉猎过：对于向量参数$\boldsymbol{w}\in\mathbb{R}^n$，我们将下一步的更新规则定义为
\begin{equation}\boldsymbol{w}_{t+1} = \mathop{\text{argmin}}_{\boldsymbol{w}} \frac{\Vert\boldsymbol{w} - \boldsymbol{w}_t\Vert^2}{2\eta_t} + \mathcal{L}(\boldsymbol{w})\end{equation}
其中$\Vert\Vert$是某个向量范数，这称为在某个范数约束下的“最速梯度下降”。接着假设$\eta_t$足够小，那么第一项占主导，这意味着$\boldsymbol{w}_{t+1}$与$\boldsymbol{w}_t$会很接近，于是我们假设$\mathcal{L}(\boldsymbol{w})$的一阶近似够用了，于是问题简化成
\begin{equation}\boldsymbol{w}_{t+1} = \mathop{\text{argmin}}_{\boldsymbol{w}} \frac{\Vert\boldsymbol{w} - \boldsymbol{w}_t\Vert^2}{2\eta_t} + \mathcal{L}(\boldsymbol{w}_t) + \nabla_{\boldsymbol{w}_t}\mathcal{L}(\boldsymbol{w}_t)^{\top}(\boldsymbol{w}-\boldsymbol{w}_t)\end{equation}
记$\Delta\boldsymbol{w}_{t+1} = \boldsymbol{w}_{t+1}-\boldsymbol{w}_t, \boldsymbol{g}_t = \nabla_{\boldsymbol{w}_t}\mathcal{L}(\boldsymbol{w}_t)$，那么可以简写成
\begin{equation}\Delta\boldsymbol{w}_{t+1} = \mathop{\text{argmin}}_{\Delta\boldsymbol{w}} \frac{\Vert\Delta\boldsymbol{w}\Vert^2}{2\eta_t} + \boldsymbol{g}_t^{\top}\Delta\boldsymbol{w}\end{equation}
计算$\Delta\boldsymbol{w}_{t+1}$的一般思路是求导，但《Old Optimizer, New Norm: An Anthology》提供了一个不用求导的统一方案：将$\Delta\boldsymbol{w}$分解为范数$\gamma = \Vert\Delta\boldsymbol{w}\Vert$和方向向量$\boldsymbol{\phi} = -\Delta\boldsymbol{w}/\Vert\Delta\boldsymbol{w}\Vert$，于是
\begin{equation}\min_{\Delta\boldsymbol{w}} \frac{\Vert\Delta\boldsymbol{w}\Vert^2}{2\eta_t} + \boldsymbol{g}_t^{\top}\Delta\boldsymbol{w} = \min_{\gamma\geq 0, \Vert\boldsymbol{\phi}\Vert=1} \frac{\gamma^2}{2\eta_t} - \gamma\boldsymbol{g}_t^{\top}\boldsymbol{\phi} = \min_{\gamma\geq 0} \frac{\gamma^2}{2\eta_t} - \gamma\bigg(\underbrace{\max_{\Vert\boldsymbol{\phi}\Vert=1}\boldsymbol{g}_t^{\top}\boldsymbol{\phi}}_{\text{记为}\Vert \boldsymbol{g}_t\Vert^{\dagger}}\bigg)\end{equation}
$\gamma$只是一个标量，跟学习率类似，容易求得最优值是$\eta_t\Vert \boldsymbol{g}_t\Vert^{\dagger}$，而更新方向则是最大化$\boldsymbol{g}_t^{\top}\boldsymbol{\phi}$（$\Vert\boldsymbol{\phi}\Vert=1$）的$\boldsymbol{\phi}^*$。现在代入欧氏范数即$\Vert\boldsymbol{\phi}\Vert_2 = \sqrt{\boldsymbol{\phi}^{\top}\boldsymbol{\phi}}$，我们就有$\Vert \boldsymbol{g}_t\Vert^{\dagger}=\Vert \boldsymbol{g}_t\Vert_2$和$\boldsymbol{\phi}^* = \boldsymbol{g}_t/\Vert\boldsymbol{g}_t\Vert_2$，这样一来$\Delta\boldsymbol{w}_{t+1}=-\eta_t \boldsymbol{g}_t$，即梯度下降（SGD）。一般地，对于$p$范数
\begin{equation}\Vert\boldsymbol{\phi}\Vert_p = \sqrt[\uproot{10}p]{\sum_{i=1}^n |\phi_i|^p}\end{equation}Hölder不等式给出$\boldsymbol{g}^{\top}\boldsymbol{\phi} \leq \Vert \boldsymbol{g}\Vert_q \Vert \boldsymbol{\phi}\Vert_p$，其中$1/p + 1/q = 1$，利用它我们得到
\begin{equation}\max_{\Vert\boldsymbol{\phi}\Vert_p=1}\boldsymbol{g}^{\top}\boldsymbol{\phi} = \Vert \boldsymbol{g}\Vert_q\end{equation}
等号成立的条件是
\begin{equation}\boldsymbol{\phi}^* = \frac{1}{\Vert\boldsymbol{g}\Vert_q^{q/p}}\Big[\text{sign}(g_1) |g_1|^{q/p},\text{sign}(g_2) |g_2|^{q/p},\cdots,\text{sign}(g_n) |g_n|^{q/p}\Big]\end{equation}
以它为方向向量的优化器叫做pbSGD，可参考《pbSGD: Powered Stochastic Gradient Descent Methods for Accelerated Non-Convex Optimization》。特别地，当$p\to\infty$时有$q\to 1$和$|g_i|^{q/p}\to 1$，此时退化为SignSGD，即SignSGD实际上是$\Vert\Vert_{\infty}$范数下的最速梯度下降。

矩阵范数 #

现在让我们将目光切换到矩阵参数$\boldsymbol{W}\in\mathbb{R}^{n\times m}$。类似地，我们将它的更新规则定义为
\begin{equation}\boldsymbol{W}_{t+1} = \mathop{\text{argmin}}_{\boldsymbol{W}} \frac{\Vert\boldsymbol{W} - \boldsymbol{W}_t\Vert^2}{2\eta_t} + \mathcal{L}(\boldsymbol{W})\end{equation}
此时$\Vert\Vert$是某种矩阵范数。同样使用一阶近似，我们得到
\begin{equation}\Delta\boldsymbol{W}_{t+1} = \mathop{\text{argmin}}_{\Delta\boldsymbol{W}} \frac{\Vert\Delta\boldsymbol{W}\Vert^2}{2\eta_t} + \text{Tr}(\boldsymbol{G}_t^{\top}\Delta\boldsymbol{W})\end{equation}
这里$\Delta\boldsymbol{W}_{t+1} = \boldsymbol{W}_{t+1}-\boldsymbol{W}_t, \boldsymbol{G}_t = \nabla_{\boldsymbol{W}_t}\mathcal{L}(\boldsymbol{W}_t)$。还是使用“范数-方向”解耦，即设$\gamma = \Vert\Delta\boldsymbol{w}\Vert$和$\boldsymbol{\Phi} = -\Delta\boldsymbol{W}/\Vert\Delta\boldsymbol{W}\Vert$，我们得到
\begin{equation}\min_{\Delta\boldsymbol{W}} \frac{\Vert\Delta\boldsymbol{W}\Vert^2}{2\eta_t} + \text{Tr}(\boldsymbol{G}_t^{\top}\Delta\boldsymbol{W}) = \min_{\gamma\geq 0} \frac{\gamma^2}{2\eta_t} - \gamma\bigg(\underbrace{\max_{\Vert\boldsymbol{\Phi}\Vert=1}\text{Tr}(\boldsymbol{G}_t^{\top}\boldsymbol{\Phi})}_{\text{记为}\Vert \boldsymbol{G}_t\Vert^{\dagger}}\bigg)\end{equation}
然后就是具体范数具体分析了。矩阵常用的范数有两种，一种是F范数，它实际上就是将矩阵展平成向量后算的欧氏范数，这种情况下结论跟向量是一样的，答案就是SGD，这里不再展开；另一种则是由向量范数诱导出来的$2$范数，也称谱范数：
\begin{equation}\Vert \boldsymbol{\Phi}\Vert_2 = \max_{\Vert \boldsymbol{x}\Vert_2 = 1} \Vert \boldsymbol{\Phi}\boldsymbol{x}\Vert_2\end{equation}
注意右端出现的$\Vert\Vert_2$的对象都是向量，所以定义是明确的。更多关于$2$范数的讨论可以参考《深度学习中的Lipschitz约束：泛化与生成模型》和《低秩近似之路（二）：SVD》。由于$2$范数是由“矩阵-向量”乘法诱导出来的，因此它更贴合矩阵乘法，并且还恒成立$\Vert\boldsymbol{\Phi}\Vert_2\leq \Vert\boldsymbol{\Phi}\Vert_F$，即$2$范数相比$F$范数更紧凑。

所以，接下来我们就针对$2$范数进行计算。设$\boldsymbol{G}$的SVD为$\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^{\top} = \sum\limits_{i=1}^r \sigma_i \boldsymbol{u}_i \boldsymbol{v}_i^{\top}$，我们有
\begin{equation}\text{Tr}(\boldsymbol{G}^{\top}\boldsymbol{\Phi})=\text{Tr}\Big(\sum_{i=1}^r \sigma_i \boldsymbol{v}_i \boldsymbol{u}_i^{\top}\boldsymbol{\Phi}\Big) = \sum_{i=1}^r \sigma_i \boldsymbol{u}_i^{\top}\boldsymbol{\Phi}\boldsymbol{v}_i\end{equation}
根据定义，当$\Vert\boldsymbol{\Phi}\Vert_2=1$时$\Vert\boldsymbol{\Phi}\boldsymbol{v}_i\Vert_2\leq \Vert\boldsymbol{v}_i\Vert_2=1$，于是$\boldsymbol{u}_i^{\top}\boldsymbol{\Phi}\boldsymbol{v}_i\leq 1$，因此
\begin{equation}\text{Tr}(\boldsymbol{G}^{\top}\boldsymbol{\Phi})\leq \sum_{i=1}^r \sigma_i\end{equation}
等号在所有$\boldsymbol{u}_i^{\top}\boldsymbol{\Phi}\boldsymbol{v}_i$都等于1时取到，此时
\begin{equation}\boldsymbol{\Phi} = \sum_{i=1}^r \boldsymbol{u}_i \boldsymbol{v}_i^{\top} = \boldsymbol{U}_{[:,:r]}\boldsymbol{V}_{[:,:r]}^{\top} = \text{msign}(\boldsymbol{G})\end{equation}
至此，我们证明了$2$范数惩罚下的梯度下降正是$\beta=0$时的Muon优化器！当$\beta > 0$时，滑动平均生效，我们可以将它视为梯度的一种更精准的估计，所以改为对动量取$\text{msign}$。总的来说，Muon相当于$2$范数约束下的梯度下降，$2$范数更好地度量了矩阵之间的本质差异，从而使每一步都走得更精准、更本质。

追根溯源 #

Muon还有一个更久远的相关工作《Shampoo: Preconditioned Stochastic Tensor Optimization》，这是2018年的论文，提出了名为Shampoo的优化器，跟Muon有异曲同工之处。

Adam通过梯度平方的平均来自适应学习率的策略，最早提出自Adagrad的论文《Adaptive Subgradient Methods for Online Learning and Stochastic Optimization》，里边提出的是直接将梯度平方累加的策略，这相当于全局等权平均，后来的RMSProp、Adam则类比动量的设计，改为滑动平均，发现在实践中表现更好。

不仅如此，Adagrad最开始提出的实际是累加外积$\boldsymbol{g}\boldsymbol{g}^{\top}$，只不过缓存外积空间成本太大，所以实践中改为Hadamard积$\boldsymbol{g}\odot\boldsymbol{g}$。那累加外积的理论依据是什么呢？这我们在《从Hessian近似看自适应学习率优化器》推导过，答案是“梯度外积的长期平均$\mathbb{E}[\boldsymbol{g}\boldsymbol{g}^{\top}]$近似了Hessian矩阵的平方$\sigma^2\boldsymbol{\mathcal{H}}_{\boldsymbol{\theta}^*}^2$”，所以这实际上在近似二阶的Newton法。

Shampoo传承了Adagrad缓存外积的思想，但考虑到成本问题，取了个折中。跟Muon一样，它同样是针对矩阵（以及高阶张量）进行优化，策略是缓存梯度的矩阵乘积$\boldsymbol{G}\boldsymbol{G}^{\top}$和$\boldsymbol{G}^{\top}\boldsymbol{G}$，而不是外积，这样空间成本是$\mathcal{O}(n^2 + m^2)$而不是$\mathcal{O}(n^2 m^2)$：
\begin{equation}\begin{aligned}
\boldsymbol{L}_t =&\, \beta\boldsymbol{L}_{t-1} + \boldsymbol{G}_t\boldsymbol{G}_t^{\top} \\[5pt]
\boldsymbol{R}_t =&\, \beta\boldsymbol{R}_{t-1} + \boldsymbol{G}_t^{\top}\boldsymbol{G}_t \\[5pt]
\boldsymbol{W}_t =&\, \boldsymbol{W}_{t-1} - \eta_t \boldsymbol{L}_t^{-1/4}\boldsymbol{G}_t\boldsymbol{R}_t^{-1/4} \\
\end{aligned}\end{equation}
这里的$\beta$是笔者自己加的，Shampoo默认了$\beta=1$，${}^{-1/4}$同样是矩阵的幂运算，可以用SVD来完成。由于Shampoo没有提出Newton-schulz迭代之类的近似方案，是直接用SVD算的，所以为了节省计算成本，它并没有每一步都计算$\boldsymbol{L}_t^{-1/4}$和$\boldsymbol{R}_t^{-1/4}$，而是间隔一定步数才更新它们的结果。

特别地，当$\beta=0$时，Shampoo的更新向量为$(\boldsymbol{G}\boldsymbol{G}^{\top})^{-1/4}\boldsymbol{G}(\boldsymbol{G}^{\top}\boldsymbol{G})^{-1/4}$，通过对$\boldsymbol{G}$进行SVD我们可以证明
\begin{equation}(\boldsymbol{G}\boldsymbol{G}^{\top})^{-1/4}\boldsymbol{G}(\boldsymbol{G}^{\top}\boldsymbol{G})^{-1/4} = (\boldsymbol{G}\boldsymbol{G}^{\top})^{-1/2}\boldsymbol{G}= \boldsymbol{G}(\boldsymbol{G}^{\top}\boldsymbol{G})^{-1/2}=\text{msign}(\boldsymbol{G})\end{equation}
这表明$\beta=0$时Shampoo和Muon在理论上是等价的！因此，Shampoo与Muon在更新量的设计方面有着相通之处。

文章小结 #

本文介绍了最近推特上颇为热闹的Muon优化器，它专门为矩阵参数定制，目前看来比AdamW更高效，并且似乎体现了一些向量化与矩阵化的本质差异，值得学习和思考一番。

转载到请包括本文地址：https://kexue.fm/archives/10592

更详细的转载事宜请参考：《科学空间FAQ》