Muon续集：为什么我们选择尝试Muon？

本文解读一下我们最新的技术报告《Muon is Scalable for LLM Training》，里边分享了我们之前在《Muon优化器赏析：从向量到矩阵的本质跨越》介绍过的Muon优化器的一次较大规模的实践，并开源了相应的模型（我们称之为“Moonlight”，目前是一个3B/16B的MoE模型）。我们发现了一个比较惊人的结论：在我们的实验设置下，Muon相比Adam能够达到将近2倍的训练效率。

优化器的工作说多不多，但说少也不少，为什么我们会选择Muon来作为新的尝试方向呢？已经调好超参的Adam优化器，怎么快速切换到Muon上进行尝试呢？模型Scale上去之后，Muon与Adam的性能效果差异如何？接下来将分享我们的思考过程。

优化原理 #

关于优化器，其实笔者之前在《Muon优化器赏析：从向量到矩阵的本质跨越》时就有过浅评，多数优化器改进实际上都只是一些小补丁，不能说毫无价值，但终究没能给人一种深刻和惊艳的感觉。

我们需要从更贴近本质的原理出发，来思考什么才是好的优化器。直观来想，理想的优化器应当有两个特性：稳和快。具体来说，理想的优化器每一步的更新应该满足两点：1、对模型扰动尽可能小；2、对Loss贡献尽可能大。说更直接点，就是我们不希望大改模型（稳），但希望大降Loss（快），典型的“既要...又要...”。

怎么将这两个特性转化为数学语言呢？稳我们可以理解为对更新量的一个约束，而快则可以理解为寻找让损失函数下降最快的更新量，所以这可以转化为一个约束优化问题。用回前文的记号，对于矩阵参数$\boldsymbol{W}\in\mathbb{R}^{n\times m}$，其梯度为$\boldsymbol{G}\in\mathbb{R}^{n\times m}$，当参数由$\boldsymbol{W}$变成$\boldsymbol{W}+\Delta\boldsymbol{W}$时，损失函数的变化量为
\begin{equation}\text{Tr}(\boldsymbol{G}^{\top}\Delta\boldsymbol{W})\end{equation}
那么在稳的前提下寻找快的更新量，那么就可以表示为
\begin{equation}\mathop{\text{argmin}}_{\Delta\boldsymbol{W}}\text{Tr}(\boldsymbol{G}^{\top}\Delta\boldsymbol{W})\quad\text{s.t.}\quad \rho(\Delta\boldsymbol{W})\leq \eta\label{eq:least-action}\end{equation}
这里$\rho(\Delta\boldsymbol{W})\geq 0$是稳的某个指标，越小表示越稳，而$\eta$是某个小于1的常数，表示我们对稳的要求，后面我们会看到它实际上就是优化器的学习率。如果读者不介意，我们可以模仿理论物理的概念，称上述原理为优化器的“最小作用量原理（Least Action Principle）”。

矩阵范数 #

式$\eqref{eq:least-action}$唯一不确定的就是稳的度量$\rho(\Delta\boldsymbol{W})$，选定$\rho(\Delta\boldsymbol{W})$后就可以把$\Delta\boldsymbol{W}$明确求解出来（至少理论上没问题）。某种程度上来说，我们可以认为不同优化器的本质差异就是它们对稳的定义不一样。

很多读者在刚学习SGD时想必都看到过类似“梯度反方向是函数值局部下降最快的方向”的说法，放到这里的框架来看，它其实就是把稳的度量选择为矩阵的$F$范数$\Vert\Delta\boldsymbol{W}\Vert_F$，也就是说，“下降最快的方向”并不是一成不变的，选定度量后才能把它确定下来，换一个范数就不一定是梯度反方向了。

接下来的问题自然是什么范数才能最恰当地度量稳？如果我们加了强约束，那么稳则稳矣，但优化器举步维艰，只能收敛到次优解；相反如果减弱约束，那么优化器放飞自我，那么训练进程将会极度不可控。所以，最理想的情况就能找到稳的最精准指标。考虑到神经网络以矩阵乘法为主，我们以$\boldsymbol{y}=\boldsymbol{x}\boldsymbol{W}$为例，有
\begin{equation}\Vert\Delta \boldsymbol{y}\Vert = \Vert\boldsymbol{x}(\boldsymbol{W} + \Delta\boldsymbol{W}) - \boldsymbol{x}\boldsymbol{W}\Vert = \Vert\boldsymbol{x} \Delta\boldsymbol{W}\Vert\leq \rho(\Delta\boldsymbol{W}) \Vert\boldsymbol{x}\Vert\end{equation}
上式的意思是，当参数由$\boldsymbol{W}$变成$\boldsymbol{W}+\Delta\boldsymbol{W}$时，模型输出变化量为$\Delta\boldsymbol{y}$，我们寄望于这个变化量的模长能够被$\Vert\boldsymbol{x}\Vert$以及$\Delta\boldsymbol{W}$相关的一个函数$\rho(\Delta\boldsymbol{W})$控制，我们就用这个函数作为稳的指标。从线性代数我们知道，$\rho(\Delta\boldsymbol{W})$的最准确值就是$\Delta\boldsymbol{W}$的谱范数$\Vert\Delta\boldsymbol{W}\Vert_2$，代入式$\eqref{eq:least-action}$得到
\begin{equation}\mathop{\text{argmin}}_{\Delta\boldsymbol{W}}\text{Tr}(\boldsymbol{G}^{\top}\Delta\boldsymbol{W})\quad\text{s.t.}\quad \Vert\Delta\boldsymbol{W}\Vert_2\leq \eta\end{equation}
这个优化问题求解出来就是$\beta=0$的Muon：
\begin{equation}\Delta\boldsymbol{W} = -\eta\, \text{msign}(\boldsymbol{G}) = -\eta\,\boldsymbol{U}_{[:,:r]}\boldsymbol{V}_{[:,:r]}^{\top}, \quad \boldsymbol{U},\boldsymbol{\Sigma},\boldsymbol{V}^{\top} = SVD(\boldsymbol{G})\end{equation}
当$\beta > 0$时，$\boldsymbol{G}$换成动量$\boldsymbol{M}$，$\boldsymbol{M}$可以看作是对梯度更平滑的估计，所以依然可以理解为上式的结论，因此我们可以得出“Muon就是谱范数下的最速下降”的说法，至于Newton-schulz迭代之类的，则是计算上的近似，这里就不细说。详细推导我们在《Muon优化器赏析：从向量到矩阵的本质跨越》已经给出，也不再重复。

权重衰减 #

至此，我们可以回答第一个问题：为什么选择尝试Muon？因为跟SGD一样，Muon给出的同样是下降最快的方向，但它的谱范数约束比SGD的$F$范数更为精准，所以有更佳的潜力。另一方面，从“为不同的参数选择最恰当的约束”角度来改进优化器，看起来也比各种补丁式修改更为本质。

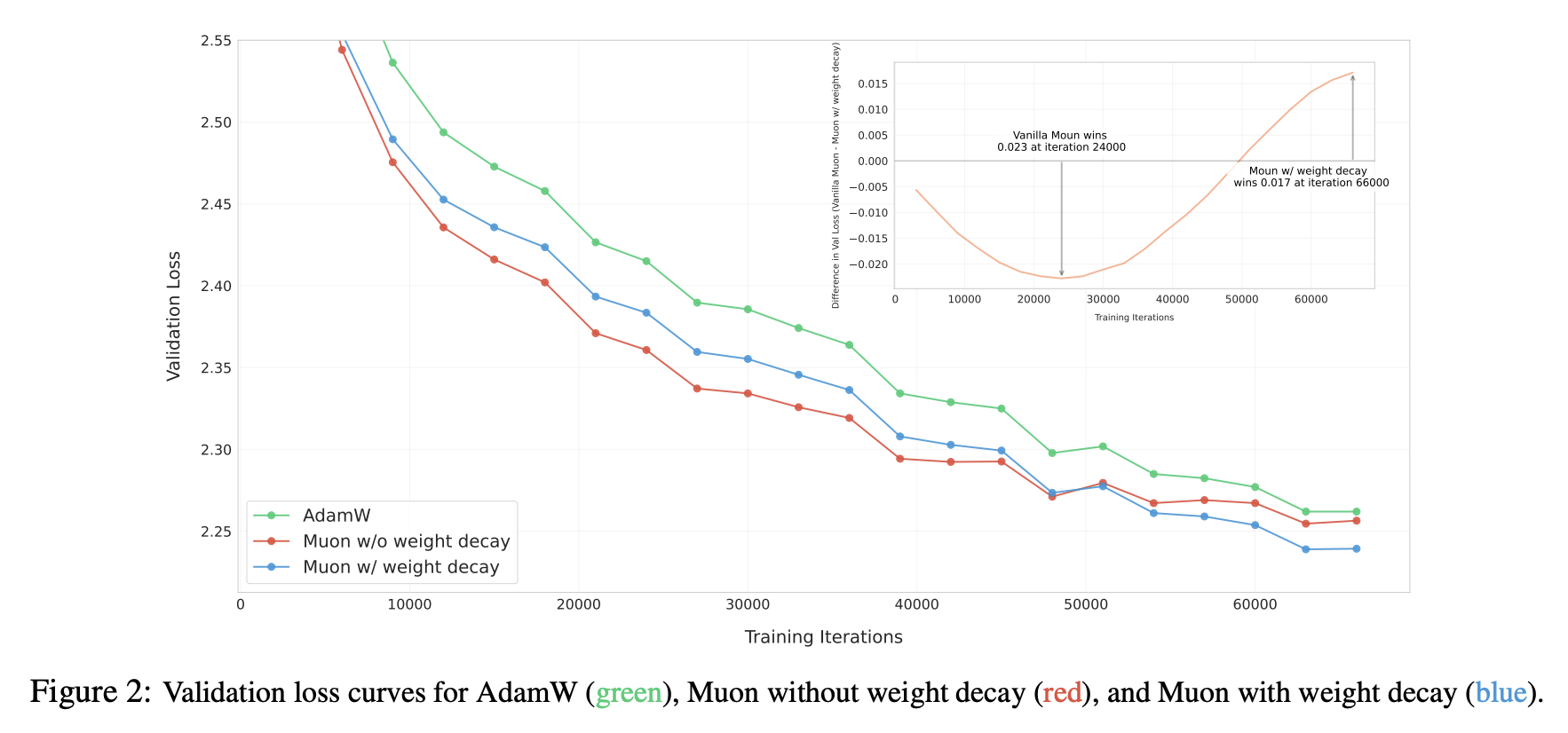
当然，潜力不意味着实力，在更大尺寸的模型上验证Muon存在一些“陷阱”。首先登场的是Weight Decay问题，尽管我们在《Muon优化器赏析：从向量到矩阵的本质跨越》介绍Muon的时候带上了Weight Decay，但实际上作者提出Muon时是没有的，而我们一开始也按照官方版本来实现，结果发现Muon前期收敛是快，但很快就被Adam追上了，而且各种“内科”还有崩溃的苗头。

我们很快意识到这可能是Weight Decay的问题，于是补上Weight Decay：
\begin{equation}\Delta\boldsymbol{W} = -\eta\, [\text{msign}(\boldsymbol{M})+ \lambda \boldsymbol{W}]\end{equation}
继续实验，果不其然，这时候Muon一直保持领先于Adam，如论文Figure 2所示：

Weight Decay起到什么作用呢？事后分析来看，可能比较关键的地方是能够让参数范数保持有界：
\begin{equation}\begin{aligned}
\Vert\boldsymbol{W}_t\Vert =&\, \Vert\boldsymbol{W}_{t-1} - \eta_t (\boldsymbol{O}_t + \lambda \boldsymbol{W}_{t-1})\Vert \\[5pt]
=&\, \Vert(1 - \eta_t \lambda)\boldsymbol{W}_{t-1} - \eta_t \lambda (\boldsymbol{O}_t/\lambda)\Vert \\[5pt]
\leq &\,(1 - \eta_t \lambda)\Vert\boldsymbol{W}_{t-1}\Vert + \eta_t \lambda \Vert\boldsymbol{O}_t/\lambda\Vert \\[5pt]
\leq &\,\max(\Vert\boldsymbol{W}_{t-1}\Vert,\Vert\boldsymbol{O}_t/\lambda\Vert) \\[5pt]
\end{aligned}\end{equation}
这里的$\Vert\cdot\Vert$是任意一种矩阵范数，即上述不等式对于任意矩阵范数都是成立的，$\boldsymbol{O}_t$是优化器给出的更新向量，对Muon来说是$\text{msign}(\boldsymbol{M})$，当我们取谱范数时，有$\Vert\text{msign}(\boldsymbol{M})\Vert_2 = 1$，所以对于Muon来说有
\begin{equation}
\Vert\boldsymbol{W}_t\Vert_2 \leq \max(\Vert\boldsymbol{W}_{t-1}\Vert_2,1/\lambda)\leq\cdots \leq \max(\Vert\boldsymbol{W}_0\Vert_2,1/\lambda)\end{equation}
这保证了模型“内科”的健康，因为$\Vert\boldsymbol{x}\boldsymbol{W}\Vert\leq \Vert\boldsymbol{x}\Vert\Vert\boldsymbol{W}\Vert_2$，$\Vert\boldsymbol{W}\Vert_2$被控制住了，意味着$\Vert\boldsymbol{x}\boldsymbol{W}\Vert$也被控制住了，就不会有爆炸的风险，这对于Attention Logits爆炸等问题也尤其重要。当然这个上界在多数情况下还是相当宽松的，实际中参数的谱范数多数会明显小于这个上界，这个不等关系只是简单显示Weight Decay有控制范数的性质存在。

RMS对齐 #

当我们决定去尝试新的优化器时，一个比较头疼的问题是如何快速找到接近最优的超参数，比如Muon至少有学习率$\eta_t$和衰减率$\lambda$两个超参数。网格搜索自然是可以，但比较费时费力，这里我们提出Update RMS对齐的超参迁移思路，可以将Adam调好的超参数用到其他优化器上。

首先，对于一个矩阵$\boldsymbol{W}\in\mathbb{R}^{n\times m}$，它的RMS（Root Mean Square）定义为
\begin{equation}\text{RMS}(\boldsymbol{W}) = \frac{\Vert \boldsymbol{W}\Vert_F}{\sqrt{nm}} = \sqrt{\frac{1}{nm}\sum_{i=1}^n\sum_{j=1}^m W_{i,j}^2}\end{equation}
简单来说，RMS度量了矩阵每个元素的平均大小。我们观察到Adam更新量的RMS是比较稳定的，通常在0.2～0.4之间，这也是为什么理论分析常用SignSGD作为Adam近似。基于此，我们建议通过RMS Norm将新优化器的Update RMS对齐到0.2：
\begin{gather}
\boldsymbol{W}_t =\boldsymbol{W}_{t-1} - \eta_t (\boldsymbol{O}_t + \lambda \boldsymbol{W}_{t-1}) \\[6pt]
\downarrow \notag\\[6pt]
\boldsymbol{W}_t = \boldsymbol{W}_{t-1} - \eta_t (0.2\, \boldsymbol{O}_t/\text{RMS}(\boldsymbol{O}_t) + \lambda \boldsymbol{W}_{t-1})
\end{gather}
这样一来，我们就可以复用Adam的$\eta_t$和$\lambda$，以达到每步对参数的更新幅度大致相同的效果。实践表明，通过这个简单策略从Adam迁移到Muon，就能训出明显优于Adam的效果，接近进一步对Muon超参进行精搜索的结果。特别地，Muon的$\text{RMS}(\boldsymbol{O}_t)=\text{RMS}(\boldsymbol{U}_{[:,:r]}\boldsymbol{V}_{[:,:r]}^{\top})$还可以解析地算出来：
\begin{equation}nm\,\text{RMS}(\boldsymbol{O}_t)^2 = \sum_{i=1}^n\sum_{j=1}^m \sum_{k=1}^r U_{i,k}^2V_{k,j}^2 = \sum_{k=1}^r\left(\sum_{i=1}^n U_{i,k}^2\right)\left(\sum_{j=1}^m V_{k,j}^2\right) = \sum_{k=1}^r 1 = r\end{equation}
即$\text{RMS}(\boldsymbol{O}_t) = \sqrt{r/nm}$，实际情况下一个矩阵严格低秩的概率比较小，因此可以认为$r = \min(n,m)$，从而有$\text{RMS}(\boldsymbol{O}_t) = \sqrt{1/\max(n,m)}$。所以我们最终没有直接用RMS Norm而是用等价的解析版本：
\begin{equation}\boldsymbol{W}_t = \boldsymbol{W}_{t-1} - \eta_t (0.2\, \boldsymbol{O}_t\,\sqrt{\max(n,m)} + \lambda \boldsymbol{W}_{t-1})\end{equation}
最后的这个式子，表明了在Muon中不适宜所有参数使用同一个学习率。比如Moonlight是一个MoE模型，有不少矩阵参数的形状都偏离方阵，$\max(n,m)$跨度比较大，如果用单一学习率，必然会导致某些参数学习过快/过慢的不同步问题，从而影响最终效果。

实验分析 #

我们在2.4B/16B这个尺寸的MoE上，对Adam和Muon做了比较充分的对比，发现Muon在收敛速度和最终效果上都有明显的优势。详细的比较结果建议大家去看原论文，这里仅截取部分分享。

Github: https://github.com/MoonshotAI/Moonlight

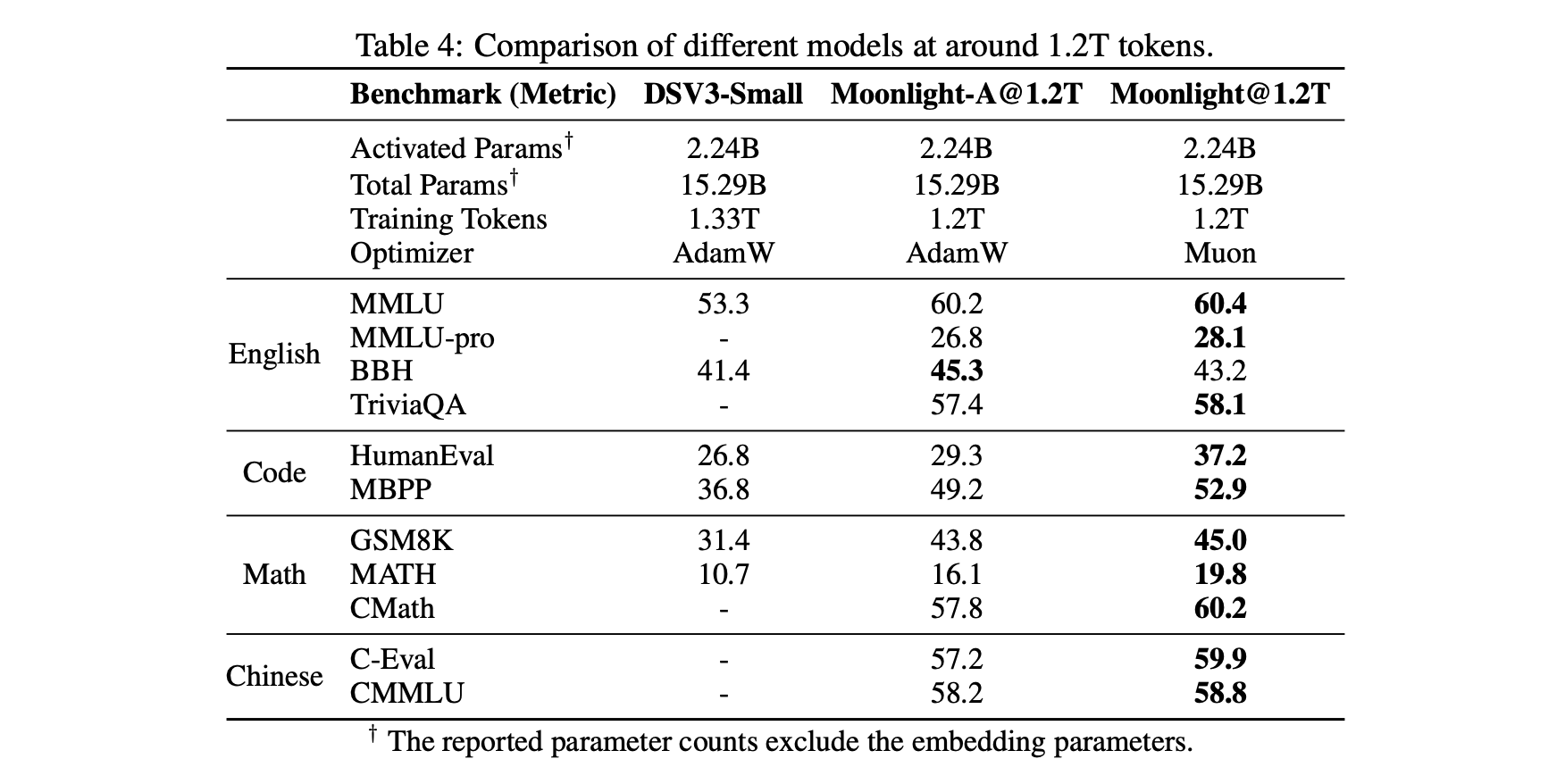
首先是一个相对客观的对照表格，包括我们自己控制变量训练的Muon和Adam的对比，以及与外界（DeepSeek）用Adam训练的同样架构的模型对比（为了便于对比，Moonlight的架构跟DSV3-Small完全一致），显示出Muon的独特优势：

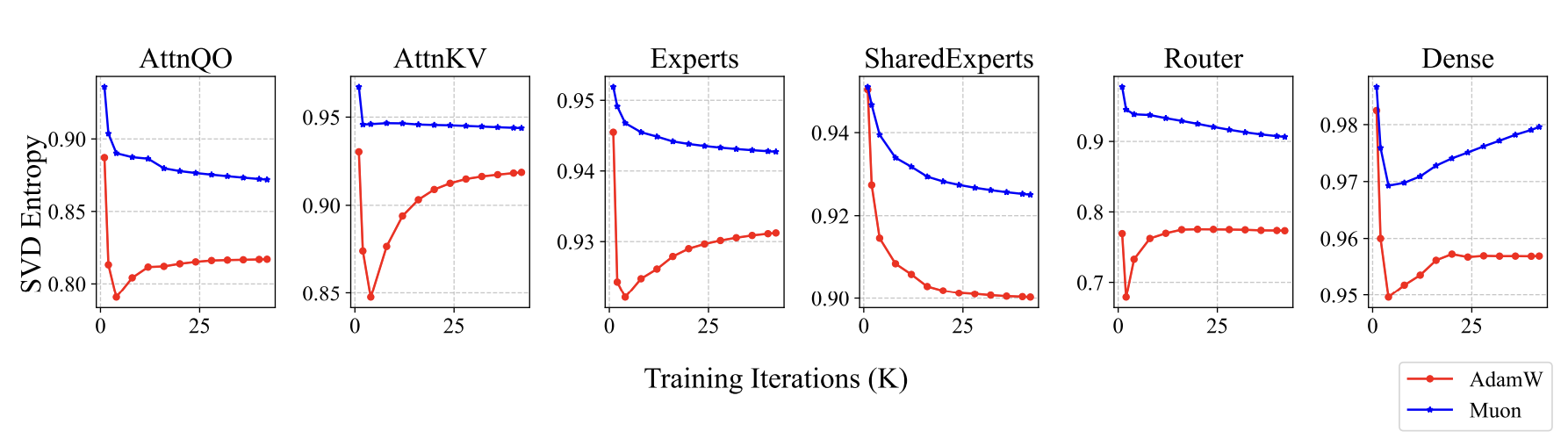
Muon训练出来的模型有什么不同呢？既然前面我们说Muon是谱范数下的最速下降，谱范数是最大的奇异值，所以我们想到了监控和分析奇异值。果然，我们发现了一些有趣的信号，Muon训出来的参数，奇异值分布相对更均匀一些，我们使用奇异值熵来定量描述这个现象：
\begin{equation}H(\boldsymbol{\sigma}) = -\frac{1}{\log n}\sum_{i=1}^n \frac{\sigma_i^2}{\sum_{j=1}^n\sigma_j^2}\log \frac{\sigma_i^2}{\sum_{j=1}^n\sigma_j^2}\end{equation}
这里$\boldsymbol{\sigma}=(\sigma_1,\sigma_2,\cdots,\sigma_n)$是某个参数的全体奇异值。Muon训出来的参数熵更大，即奇异值分布更均匀，意味着这个参数越不容易压缩，这说明Muon更充分发挥了参数的潜能：

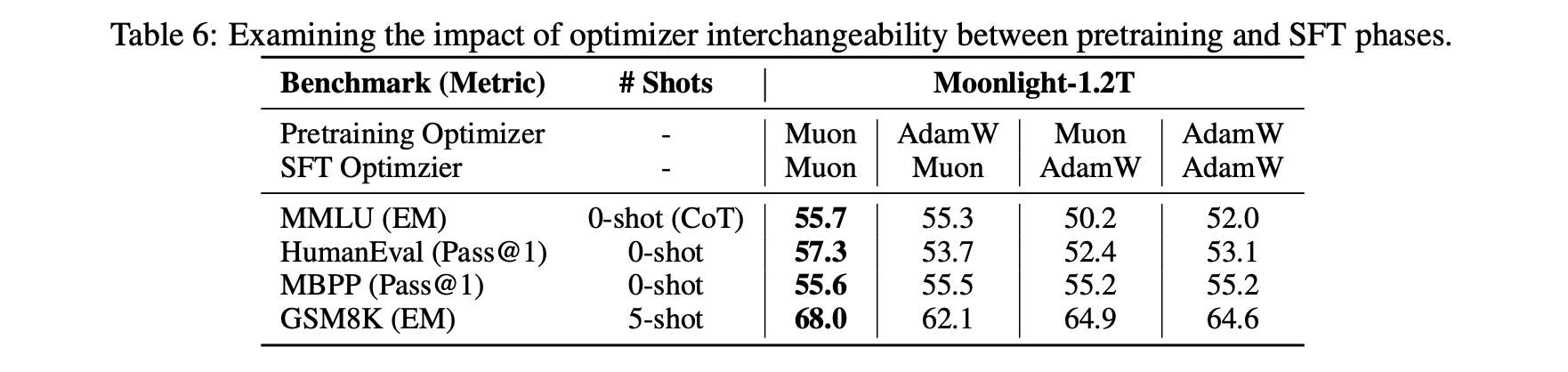
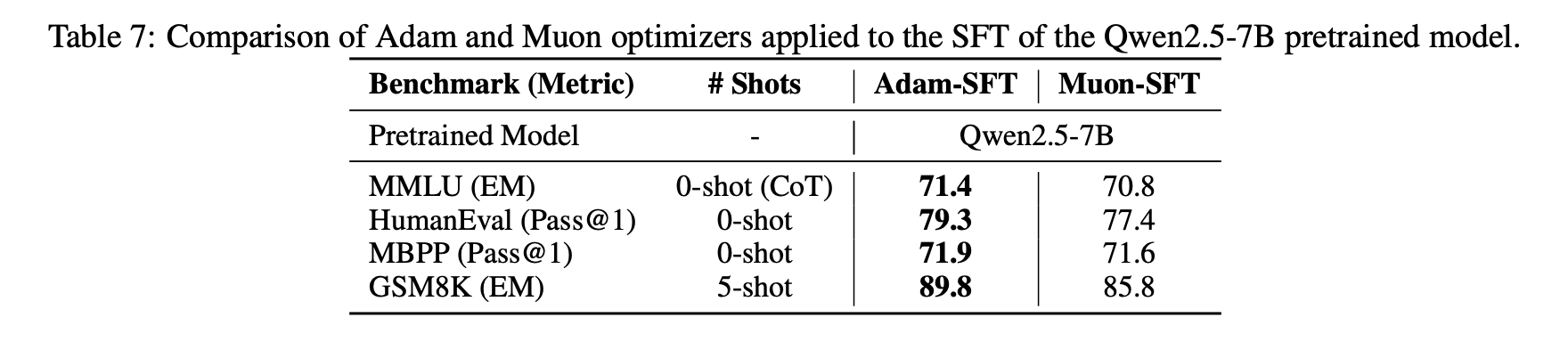
还有一个有趣的发现是当我们将Muon用于微调（SFT）时，可能会因为预训练没用Muon而得到次优解。具体来说，如果预训练和微调都用Muon，那么表现是最好的，但如果是另外三种组合（Adam+Muon、Muon+Adam、Adam+Adam），其效果优劣没有呈现于明显的规律。

这个现象表明存在一些特殊的初始化对Muon不利，当然反过来也可能存在一些初始化对Muon更有利，更底层的原理我们还在探索中。

拓展思考 #

总的来说，在我们的实验里，Muon的表现跟Adam相比显得非常有竞争力。作为一个形式上跟Adam差异较大的新优化器，Muon的这个表现其实不单单是“可圈可点”了，还表明它可能捕捉到了一些本质的特性。

此前，社区流传着一个观点：Adam之所以表现好，是因为主流的模型架构改进都在“过拟合”Adam。这个观点最早应该出自《Neural Networks (Maybe) Evolved to Make Adam The Best Optimizer》，看上去有点荒谬，但实际上意蕴深长。试想一下，当我们尝试改进模型后，就会拿Adam训一遍看效果，效果好就保留，否则放弃。可这个效果好，究竟是因为它本质更佳，还是因为它更匹配Adam了呢？

这就有点耐人寻味了。当然不说全部，肯定至少有一部份工作，是因为它跟Adam更配而表现出更好的效果，所以久而久之，模型架构就会朝着一个有利于Adam的方向演进。在这个背景下，一个跟Adam显著不同的优化器还能“出圈”，就尤其值得关注和思考了。注意笔者和所在公司都不属Muon提出者，所以这番言论纯属“肺腑之言”，并不存在自卖自夸的意思。

接下来Muon还有什么工作可做呢？其实应该还有不少。比如上面提到的“Adam预训练+Muon微调”效果不佳问题，进一步分析还是有必要和有价值的，毕竟现在大家开源的模型权重基本都是Adam训的，如果Muon微调不行，必然也影响它的普及。当然了，我们还可以借着这个契机进一步深化对Muon理解（面向Bug学习）。

还有一个推广的思考，就是Muon基于谱范数，谱范数是最大奇异值，事实上基于奇异值我们还可以构造一系列范数，如Schatten范数，将它推广到这种更广义的范数然后进行调参，理论上还有机会取得更好的效果。此外，Moonlight发布后，还有一些读者问到Muon下µP（maximal update parametrization）如何设计，这也是一个亟待解决的问题。

文章小结 #

本文介绍了我们在Muon优化器上的一次较大规模实践（Moonlight），并分享了我们对Muon优化器的最新思考。

转载到请包括本文地址：https://kexue.fm/archives/10739

更详细的转载事宜请参考：《科学空间FAQ》