三次方程的三角函数解法

对于解方程，代数学家希望能够从理论上证明解的存在性以及解的求法，所以就有了1到4次方程的求根公式、5次及以上的代数方程没有根式可解等重要理论；然而，通常的学者（如物理学家、天文学家）都不需要这些内容，他们只关心如何尽可能快地求出指定方程的根（尤其是实数根），所以他们通常关注的是方程的数值算法，当然，如果能有一个相对简单的求根公式，也是他们所希望的。而接下来所要介绍的内容，则是满足了这一需要的三次方程的求根公式，其中用到的相当一部分的理论，是与三角函数相关的。

储备 #

\begin{equation}\frac{2}{\tan 2A}=\frac{1}{\tan A}-\tan A\end{equation}
\begin{equation}\frac{2}{\sin 2A}=\frac{1}{\tan A}+\tan A\end{equation}
\begin{equation}\cos(3A)=4\cos^3 A-3\cos A\end{equation}

思路 #

在这里我们只是讨论三次方程$x^3+ax^2+bx=c$的解法，原因在于这种三次方程在实际应用中更具有代表性。任意的这样的一道三次方程可以通过变换变成$y^3+mx=n$的形式，接着变成$z^3\pm 3z=p$的形式，$z^3\pm 3z=p$能够有相对简单的解法，所以就把三次方程的根相对简单地解出来（记住，这里一直强调“相对”，因为三次方程的解法再简单也不可能比二次方程的求根公式简单...）

变换 #

一、$x^3+ax^2+bx=c \to y^3+mx=n$

其实很简单，只要设$x=y-a/3$，代入原方程，得到：
$$y^3+(b-\frac{a^2}{3})y=c+\frac{ab}{3}-\frac{2a^3}{27}$$
对比$y^3+mx=n$，不难发现：
$$m=b-\frac{a^2}{3},n=c+\frac{ab}{3}-\frac{2a^3}{27}$$
变换完成。

二、$y^3+mx=n \to z^3\pm 3z=p$

这里的“$\pm $”与m的符号相同。令$y=\lambda z$，代入并整理，得到$z^3+\frac{m}{\lambda^2}=\frac{n}{\lambda^3}$，对比$z^3\pm 3z=p$，就可以得到：
$$\begin{aligned}\frac{m}{\lambda^2}=\pm 3&,\frac{n}{\lambda^3}=p\\
\lambda=|m/3|^{(1/2)}&,p=n|\frac{3}{m}|^{(3/2)}\end{aligned}$$
变换完成。

解答 #

现在问题集中到解$z^3\pm 3z=p$类型的方程上了，我们需要分开来讨论。

x^3+3x的图像

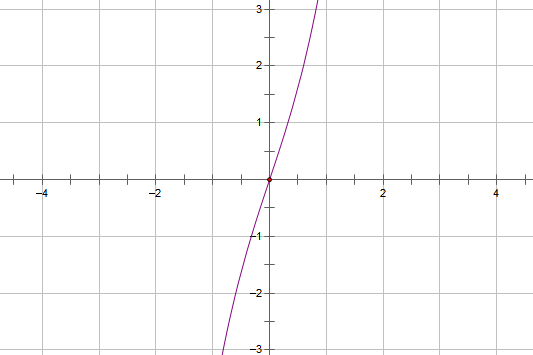
首先考虑$z^3+3z=p$，令$z=A^{-1}-A$，代入方程后整理得到$A^{-3}-A^3=p$，通过换元可以将其变为一元二次方程。但我们不这样做，令$A^3=\tan B$，利用“知识储备”的公式(1)，变成$\frac{2}{\tan 2B}=\frac{1}{\tan B}-\tan B=p$，即$\tan 2B=\frac{2}{p}$，反推得$A=(\tan \frac{\arctan \frac{2}{p}}{2})^{(1/3)}$。至此，解答完毕。从图像可以看出，对于所有的p，该方程都有且只有一个实数根。

接着考虑$z^3-3z=p$，令$z=A^{-1}+A$，代入方程后整理得到$A^{-3}+A^3=p$，同样通过换元可以将其变为一元二次方程。而我们模仿上述做法，令$A^3=\tan B$，利用“知识储备”的公式(2)，变成$\frac{2}{\sin 2B}=\frac{1}{\tan B}+\tan B=p$，即$\sin 2B=\frac{2}{p}$，反推得$A=(\tan \frac{\arcsin\frac{2}{p}}{2})^{(1/3)}$。

x^3-3x的图像

也许有朋友认为到此已经解答完成了。然而我们注意到，上一步中的A表达式中有一项是$\arcsin\frac{2}{p}$，这仅仅对$|p|> 2$奏效。但从图像可以看出，当$|p|\leq 2$时，该方程并非无实数根，而是有2~3个实数根。这样就需要我们寻找另一种方法来解决这个特殊情况。这一次，我们利用到了知识储备中的公式(3)。方程$z^3-3z=p$可以改写成$4(z/2)^2-3(z/2)=p/2$，这样每一项的系数都与公式(3)对应，这样我们就有$\cos 3A=p/2,2\cos A=z$，反推得到$z=2\cos(\frac{\arccos (p/2)+2k\pi}{3}),(k=0,1,2)$，这样就得到了三个实数根了。至此，三次方程的求解基本完成。

汇总 #

在这里把上面的过程整理一下：

对于一般的三次方程$x^3+ax^2+bx=c$，先做以下计算
$$m=b-\frac{a^2}{3},n=c+\frac{ab}{3}-\frac{2a^3}{27},p=n|\frac{3}{m}|^{(3/2)}$$

m是正数或0表明该方程只有1个实数根，执行第(I)步；m是负数，且p>2则说明该方程的有1个实数根，p=2则说明该方程有2个实数根，p<2说明该方程有3个实数根，执行第(II)步；当m=0时候，该方程有1个实数根，执行第(III)步

(I).(m>0)
$$\begin{aligned}A=(\tan \frac{\arctan \frac{2}{p}}{2})^{(1/3)},z=A^{-1}-A \\ x=|m/3|^{(1/2)}z-a/3\end{aligned}$$

(II).1.(m<0,|p|>2)
$$\begin{aligned}A=(\tan \frac{\arcsin\frac{2}{p}}{2})^{(1/3)},z=A^{-1}+A \\ x=|m/3|^{(1/2)}z-a/3\end{aligned}$$

(II).2.(m<0,|p|<2)
$$\begin{aligned}z=2\cos(\frac{\arccos (p/2)+2k\pi}{3}),(k=0,1,2) \\ x=|m/3|^{(1/2)}z-a/3\end{aligned}$$

(III).(m=0)
$$x=\sqrt[3]{n}-\frac{a}{3}$$

结论 #

经过上述变换和求解，我们可以发现，任何实系数三次方程都可以变换成$z^3\pm 3z=p$的形式（p是实数），而$z^3\pm 3z=p$总有一个实数根，也就是说我们藉此也证明了任何三次方程都有不少于一个实数根。

也许有人问，我想求出非实数根要怎样做呢？这其实可以利用韦达定理，对于三次方程$x^3+ax^2+bx=c$的三个根，有以下关系：
$$x_1 x_2 x_3=c;x_1+x_2+x_3=-a$$
如果已经知道一个实数根，那么上式就成为了一个二元二次方程组，可以轻松地求出。在此不再详述。

把三角函数与三次方程求根相结合，这思路来源已久，只是一直未能将其一般化。通过研究《天体力学引论》，我得到了灵感，并且通过网络，我找到了相关公式，把这些搜寻到的资料整理起来，就得到了眼前的这一套求三次方程根的解法。由于所用到的公式之中，没有任何一条是我自己“独创”的，因此不敢狂妄地称“自创”了新解法。灵感也只是来源于对解方程的执着以及网络以及书籍的帮助，所以实在不值一提。但是仍然希望读者阅读或转载时能够链接一下科学空间，让更多的人认识科学空间^_^。

转载到请包括本文地址：https://kexue.fm/archives/831

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。