有限Vs无限:无穷电荷板的场|平行板电容

学过高中物理的同学都会知道，在经典力学和静电学理论中，万有引力和库仑力有着类似的性质，它们都与距离平方成反比。现在我从引力角度向大家提出一个问题：

一块密度均匀的无限大的平面板，它所产生的引力场是否均匀的？也就是说，板外任意一点的等质量物体受到的引力是否相同？

对于静电力也可以提出类似的问题，只要把引力换成库仑力，把质量换成电荷即可。只要类比有限的情况，我们就会得出结论：场一定是不均匀的！因为力与距离平方成反比，距离不同，受力就不等。果真如此吗？

事实往往出人意外，这是一个典型的说明有限与无限有天壤之别的例子：场居然是均匀的！！

一、初等证明

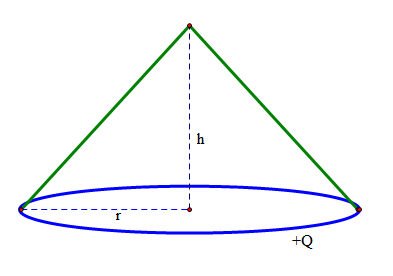
已经学习了多重积分的朋友，可以通过二重积分来计算这一结果，结果就会发现场与距离无关。不过，为了照顾仅仅有一些基本微积分和物理知识的朋友，BoJone决定介绍一个自己想出的相对“初等”的证明方法。首先我们考虑一个半径为r，高h的正圆锥。它的底面圆周上均匀分布着总电荷量为+Q的电荷。

由于各向同性的原因，我们可以很快地写出其顶点上的场强为：
$$E'=\frac{kQh}{(r^2+h^2)^{3//2}}$$

换言之，就是只取竖直方向的分力，因为水平方向的分力都被相互抵消了。该场强的方向为竖直向上。

一个无穷大的、电荷密度为$\sigma $的平面板可以看成无限个半径不等、宽度很小的圆环组成。其上方任意一点可以与这些圆组成无限个正圆锥。其总场强E应该为各圆锥场强的叠加。各圆锥场强近似为
$$\Delta E=k\frac{2\pi r\sigma h}{(r^2+h^2)^{3//2}}\Delta r$$

因此$E=\int_0^{+\infty}\frac{2k\pi\sigma hr}{(r^2+h^2)^{3//2}} dr=2k\pi\sigma$

最后的结果是一个常数，这就是出人意料的匀强电场！（各位体验到有限与无限的区别了吧？）

二、进一步理解

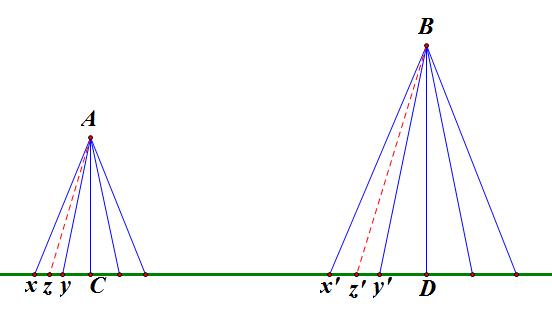
不排除有这样的可能，即有的读者仍然不相信或者是不能理解上述结果。BoJone企图再通过一个图来“说明”（而不用计算）这的的确确是一个匀强的场。如上图，我们的目的是证明A点与B点的受力情况是一样的。首先我们分别作出A点与B点在平面的正投影点（图中是只画出了二维，实际是三维），然后以投影点为中心，将平面划分成一个个等圆。其中半径与距离成正比。如图中$\frac{xz}{x'z'}=\frac{AC}{BD}$。

由图得到：圆xy对A点和圆x'y'对B点的场强方向都是$\vec{zA}$，而且大小相等（因为A点的距离小一点，但是圆xy的电荷量也少一点。库仑力与长度平方成反比，而电荷量与长度平方成正比，两者抵消）。也就是说，A点的每一个方向的受力，都可以在B点的位置上找到一个等效的受力（记住是无穷大的面）。因此两点的场强相等。

三、足够大平行板的电容

经过上述计算得，如果有两块无限大的平行板，电荷的面密度均为$\sigma$，电性相反，可知板间场强为$4k\pi\sigma$

当两块有限平行板较大时，$4k\pi\sigma$仍然是其板间场强的一个相当好的近似（特别是中心处）。设其正对面积为S，距离为d，$Q=\sigma S$，电容为
$$C=\frac{Q}{U}=\frac{Q}{Ed}=\frac{Q}{4k\pi\sigma d}=\frac{S}{4k\pi d}$$

这就是高中课本提供的用来计算平行板电容的公式！当然这里默认了两板间为真空。若为非真空，则需要乘上一个修正因子，即$C=\frac{\varepsilon S}{4k\pi d}$

以上是BoJone在2011.02.22的计算结果，其中得到了《费恩曼物理讲义》第二卷的启示。

转载到请包括本文地址：https://kexue.fm/archives/1271

更详细的转载事宜请参考：《科学空间FAQ》