混沌的世界——“星之轨迹”的研究

（本文已被刊登在2012年1月的《天文爱好者》上，于笔者而言这是一份很棒的新年礼物！）

在去年第七期《天爱》上，我们看到了N体问题所呈现出来的一些对称、漂亮的周期轨道，这体现了N体问题和谐有序的一面。但是这仅仅是N体问题的冰山一角，笔者也提到过N体问题的本质是混沌、无序的，通俗来讲就是非常乱，无法用数学方程来精确描述。这看起来是一种不完美。但试想，探索当初伽利略将望远镜对准月球后，看到的是如想象中光滑的月面，那么他还会惊叹宇宙的神奇吗？

本文就让我们来更深入地了解一下N体问题的研究历史。

观测&拟合时代

由于人类的自我优越感以及日月星辰东升西落的经验，让我们长期都认为地球是宇宙的中心。第一个比较系统提出地心说的人当属天文学家欧多克斯（Eudoxus，死于公元前347年左右），但他的地心说是非常粗糙的，以至于无法解释很多基本现象，如无法准确预言日食和解释行星逆行等。但亚里士多德接受了地心说，并且由于他在政治和科学上的权威，使地心说免去了夭折的命运。后来托勒密通过他的本轮，完善了地心说，使之延续到了16世纪。

很多人都听说过托勒密的本轮，但未必了解其中的原理。其实托勒密的理论是一个非常“折衷”而实用的理论。由于传统的地心说认为行星在一个圆形轨道上绕地球运动，以至于无法解释行星逆行。于是托勒密想到了一个“巧妙的办法”：他认为行星是绕着一个点作匀速圆周运动的（本轮），而这个点才绕地球作圆周运动（想象一下在太阳上看月球的运动）。通过精妙设置，就可以解释行星逆行。尽管改进后精确了不少，但还是与当时的数据有些出入，所以托勒密又在最初的本轮上加上一个新的小本轮。最终通过调整40多个参数，托勒密的模型终于与当时的观测数据完全相符。要知道，托勒密在数学上绝不草率，他的模型是相当精确的，而且后来人们研究发现，把他的本轮用现代数学语言描述出来，得到的是现代高等数学中的傅里叶级数！

随着时间的推移，观测数据越来越精确，单纯对地心说进行修正已经显得力不从心了。16世纪，哥白尼提出太阳才是宇宙中心，地球和五大行星绕着太阳转，那时候哥白尼的理论显得如此简单，因为他只需要15个参数就可以解释历史上的天文现象。而在第谷?布拉赫那儿，“地心说”作了最后一次“挣扎”，第谷设想太阳绕着地球转，五大行星绕着太阳转。这本质和日心说没有区别，只是第谷不肯放弃地球的超然位置而已。后来，利用第谷的观测数据，开普勒总结出了行星运动的三定律，非常精确（至少在他那个时代）地描述了太阳系行星的运动情况，而且只用到了11个参数。

太阳系是稳定的吗？

不论是地心说、日心说还是开普勒三定律，他们都是用数学公式来对观测数据进行拟合，这不能算是用数学结合力学来严格分析天体运行。天体力学“第一人”当数牛顿，牛顿有两个强有力的工具：万有引力定律和微积分，利用它们，牛顿从数学上严格推导了开普勒三定理，从而彻底解决了二体问题。但是牛顿已经意识到，当N大于2时，问题不是一般的难，以至于他一想到三体问题就头疼。牛顿含蓄地说：“…如果我没有弄错的话，同时考虑所有对（行星）运动的影响并且使用简单计算即可得的精确定律来定义这些运动超出了人类思维所能及的范围。”

虽然N体问题很难，但是我们的太阳系是一个实实在在的多体系统，要精确描述行星、卫星等运动轨迹，只考虑二体问题显然是不够的。既然我们还没有办法解决N体问题，那么可以先来一个“折衷的办法”，考虑在二体问题的轨道上进行修正。因为我们的太阳系99.8%的质量集中在太阳，太阳是我们主要的引力源，其他大天体，如木星、土星，虽然会造成一定的影响，但是毕竟不是很大，可以视为“摄动”。于是问题就变成了研究一个绕着大质量天体运动的小天体受到第三体引力“微扰”而偏离圆锥曲线轨道的问题，这发展成为了“摄动理论”。这种方法不仅仅应用于天体力学，还渗透到了很多学科，例如在某些电子领域被称为“微扰理论”。

在19世纪80年代前，摄动理论一直是天体力学的核心之一。很多著名的数学家和力学家都对此作出了杰出的贡献，如欧拉、拉格朗日、雅可比、拉普拉斯、泊松、哈雷特等等。在这个时期，一个最著名的问题就是回答我们太阳系是一个稳定的系统吗？当然，这里的稳定讨论的不是太阳会不会爆炸之类的稳定，而是将太阳系各天体看成质点，讨论它们在相互引力作用下会不会碰撞或趋于无限距离等等。它有助于我们回答“火星或金星会不会撞上地球”之类的问题，如果真的发生了，我们就可以提前作出预报。

1773年，数学家拉普拉斯作出了第一个关于太阳系稳定的预测：在离心率的一次幂函数逼近中，行星的长轴不含有久期项。这些专业术语意味着什么呢？简单来讲，幂函数逼近的次数越高，意味着轨道的描述越精确（二体问题可以看成是0次的），而出现久期项则意味这太阳系可能是不稳定的。显然，拉普拉斯的结果给我们吃了一颗“定心丸”：至少在他的预测中，太阳系是稳定的。1774～1776年，拉格朗日对这个结果进行了推广，他的结果也表明太阳系是稳定的。1809年，法国数学家泊松又向前迈进了一步，他证明在二次逼近中行星的长轴同样不含有久期项。似乎，我们可以很放心地认为太阳系很稳定了。

但不要忘记，这都是“摄动理论”的结果，也就是近似的答案。1877年，罗马尼亚数学家哈雷特证明了在三次逼近中，行星轨道长轴出现了久期项！从而明确地得出了相反的结论：太阳系未必是稳定的！此时，N体问题的本质已经开始呈现出端倪了。接下来，我们将会看到一位伟大的法国数学家作出的划时代的贡献。

混沌初生

为了吸引更多的人参与到N体问题的解答之中，1885年，瑞典数学杂志Acta Mathematica的第七卷上出现了一则通告：为了庆祝瑞典和挪威国王奥斯卡二世在1889年的六十岁生日，Acta Mathematica将举办一次数学问题比赛，悬赏2500克郎和一块金牌，比赛的题目有四个，其中第一个就是找到N体问题的所有解。这次比赛在当时轰动一时，虽然奖金不高，这种崇高的荣誉是当时罕见的，要知道瑞典更有名的诺贝尔(Alfred Bernhard Nobel)奖是在几年后的1896年才开始评选的。但是由于问题的困难程度，大多数一开始跃跃欲试的数学家后来都知难而退，最后只有四五个数学家真正交了他们的答卷。而优胜者也并不难选出，虽然还是没有人能完整地解决任何一个问题，但是所有评委一致认为其中一份答卷对于N体问题的解决做出了关键的贡献，应该把奖颁给这位数学家。这位获胜者就是法国数学家、物理学家庞加莱(Jules Henri Poincare)。

有人说过这样的话：

“相对论消除了关于绝对空间和时间的幻想；量子力学则消除了关于可控测量过程的牛顿式的梦；而混沌则消除了拉普拉斯关于决定论式可预测的幻想。”

无疑，这是对庞加莱极高的评价。那么，庞加莱究竟作出了什么杰出贡献，以至于他得到了如此高的评价呢？因为他发现了微分方程中的混沌现象，并且发现几乎所有微分方程的解都是混沌的。这意味着什么呢？他实际上告诉我们：我们的世界几乎都是混沌的！

这里多次重复了“混沌”这个词，我们熟知的蝴蝶效应也告诉了我们一些有关混沌的消息。要是读者中有刘慈欣《三体》的忠实粉丝的话，我想你对混沌的印象会更加深刻的。现在让我们更深入一点了解混沌。

学习了高数的读者会知道，通过牛顿的微积分，已知一个质点的初始速度和位置，我们就可以描述这个物体任意时刻的运动情况（微分方程理论），这就是所谓的“决定论式”。问题就在于，测量是有精度限制的，超出精度那部分我们不知道具体细节，假如精度是0.01m/s，我们就可以把初始速度控制在v=6.82m/s，但是实际上初始速度有可能是6.821m/s，也有可能是6.822m/s，可这0.001m/s的差别回到以后物体的运动造成多大影响呢？要是影响不大的话，那么我们就说这个运动是可预测的；要是这微小的差别可以造成日后的“天壤之别”的话，那么这个运动就是不可预测的，也就是混沌的。这就好比古人所说的“失之毫厘，差之千里”。同时我们也不可能去重复这个运动，因为重复这个运动需要初始速度和位置绝对精确地对应，而我们无法做到这一点！

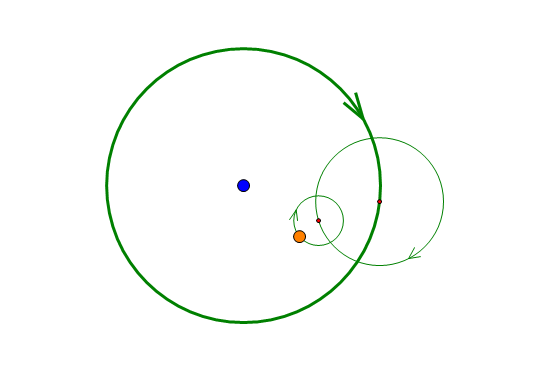
三体问题的轨道模拟，蓝色点为第三体，红线为第三体轨迹，可见不是一般的乱！

当然，这并不是说牛顿的理论是错误的，已知一个质点的初始速度和位置，我们的确可以知道它任意时刻的运动情况，只是我们永远也无法精确知道物体的初始情况。通过测量，我们也许发现两个速度是一样的，但实际上存在无法测量的微小的差别，这个差别就导致了未来的不可预测。而恰好，N体问题就是这样的一个系统，当N>2时，混沌便出现了。

有一首民谣生动地阐述了这个理论：

丢失一个钉子，坏了一只蹄铁；
坏了一只蹄铁，折了一匹战马；
折了一匹战马，伤了一位骑士；
伤了一位骑士，输了一场战斗；
输了一场战斗，亡了一个帝国。

原来，一个帝国的灭亡仅仅是因为一个钉子的丢失！

原来我们的世界都是那么地乱

庞加莱之前的数学家、天文学家们在研究物体的运动时使用的都是定量的方法，即要判断一个物体某段时间后的运动情况，你得把这个物体从现在起到那一时刻的运动都算出来。而庞加莱能够发现混沌现象，关键在于他开辟了一条与前任截然不同的道路，即用“定性”的方法来研究物体的运动。意即我只需要知道这个物体在未来的一种运动“趋势”，而不需要知道它究竟运动到了哪个点上。通俗来讲，比如我想知道两个整数相乘结果究竟是技术还是偶数，我并不需要把结果算出来，只需要看个位数字即可。

庞加莱还发现，几乎所有微分方程的解都是混沌的，这意味着我们整个世界都处于混沌之中。最明显的混沌是地球的大气运动，我们知道准确预报天气是一件极为艰难的事情，因为大气运动的不可预测性，使我们难以确知几天后究竟是雨天还是晴天。同样，地震、火山、生物的进化与繁殖、人类的思维模式等等都带有极大的不确定性，这都是混沌的例子。

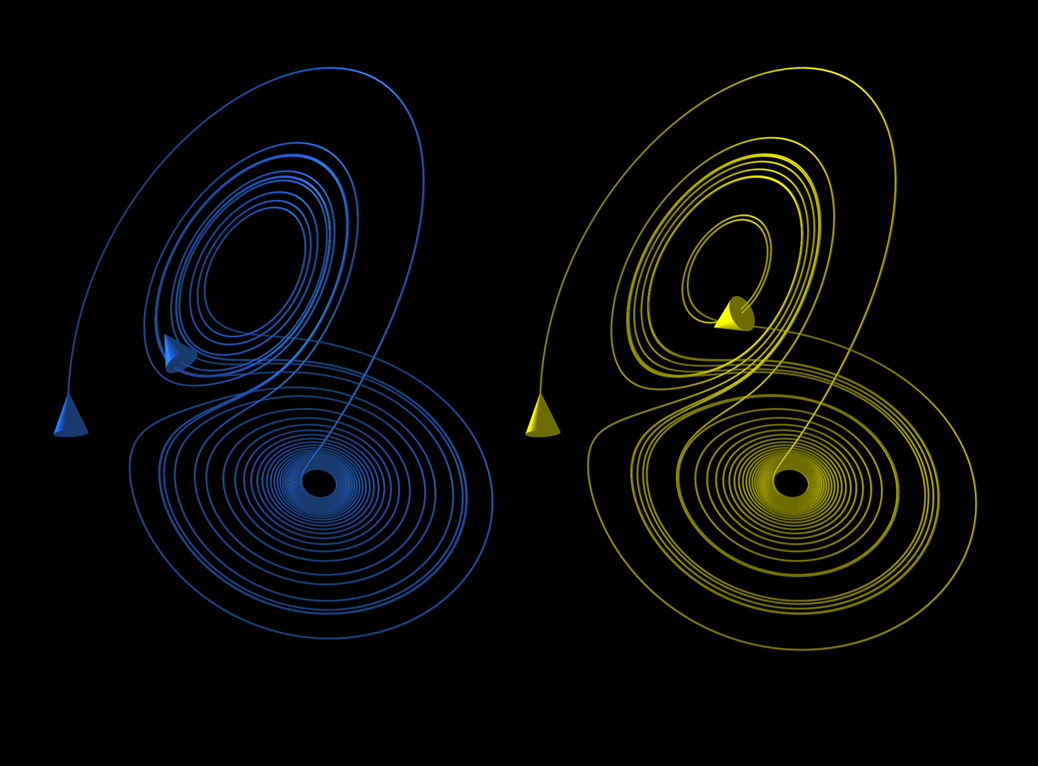
这两幅图是大气运动研究的洛伦茨吸引子中的两条轨迹（蓝色、黄色各一）的三维演变的三个时段， 这两条轨迹的初始点只在x坐标上相差10^-5。开始时，两条轨迹似乎是重合的，但是在最后，两个锥体轨迹出现极大差别。

可是我们的的确确生活在一个多体的系统中，为什么我们感受不到N体问题的混沌呢？为什么太阳系的各大行星还是那么有秩序地绕太阳作近椭圆运动？计算机模拟表明，早期的太阳系是非常混沌的，经过长期的演化，那些偏心率太大的天体，要不飞出了太阳，要不就与其他天体发生了碰撞，最终只留下了那些近圆的轨道天体了。还有另外一个原因，N体问题的稳定建立在“数量级差异”之上，以三体问题为例，要想三体系统稳定存在，只有两个办法：一个是第三体质量比前两体小很多数量级，另外就是第三体的距离比前两体大很多数量级，第三体的引力是如此地小以至于几乎可以忽略。这样的问题被称为“限制性三体问题”，也是庞加莱首次研究的。太阳系质量集中在太阳，这样就基本上满足了质量上的数量级差异的，那么它可以稳定存在很久也不意外了。

现在回到那个令人感兴趣的问题：太阳系是稳定的吗？现在对于太阳系稳定性这一数百年之久的问题我们已经有了一个确定的概率解（99%）。在接下去的5千万年里任何行星都不会失控。在太阳面对其60亿年之后的终点时，行星则确实会展现出它们不同寻常的轨迹。而剩下的1%的概率指水星的轨道会失控，有可能真的导致地球会和火星发生毁灭性的直接碰撞的发生。但那已经是上亿年后的事情了。

尾音

N体问题的故事就暂时搁笔了。随着电子计算机时代的来临，天体力学的工作已渐渐淡出了天文爱好者的视野，而转交给了计算机。因此，重温那段天体力学的往事，不仅仅让我们了解到其中的发展过程，更重要的是领会其中的思考方式的变化。天文从来就不单纯是一门科学，也同时是一门哲学。庞加莱里程碑式的结果宣告了一个新时代的来临，他带来的不仅仅是数学物理上的进步，更是一种对世界全新的思考方式。正如N体问题一样，世界是混沌的，无法预测的——我们的人生不亦如此？

参考资料：
《圆的历史——数学推理与物理推理》
《天遇——混沌与稳定性的起源》
科学松鼠会：《太阳系是稳定的吗？》

转载到请包括本文地址：https://kexue.fm/archives/1525

更详细的转载事宜请参考：《科学空间FAQ》