倒立单摆之分离频率

Mathieu方程

在文章《有质动力：倒立单摆的稳定性》中，我们分析了通过高频低幅振荡来使得倒立单摆稳定的可能性，并且得出了运动方程
$$l\ddot{\theta}+[h_0 \omega^2 \cos(\omega t)-g]\sin\theta=0$$

由此对单摆频率的下限提出了要求$\omega \gg \sqrt{\frac{g}{h_0}}$。然而，那个下限只不过是必要的，却不是充分的。如果要完整地分析该单摆的运动方程，最理想的方法当然是写出上述常微分方程的解析解。不过很遗憾，我们并没有办法做到这一点。我们只能够采取各种近似方法来求解。近似方法一般指数值计算方法，然后笔者偏爱的是解析方法，也就是说，即使是近似解，也希望能够求出近似的解析解。

首先不妨假设$\theta \ll 1$，那么可以使用近似$\sin \theta \approx \theta$，即
$$l\ddot{\theta}+[h_0 \omega^2 \cos(\omega t)-g]\theta=0$$

上述方程是一种特殊的Mathieu方程，与一般的Mathieu方程不同的是，参考书上的Mathieu方程的$g$是负数，而且$h_0 \omega^2$是小量。相反，这里的$h_0 \omega^2$是主要项，而$g$是正数。我们将采用一种特殊的技巧求得近似解析解。

数值分析

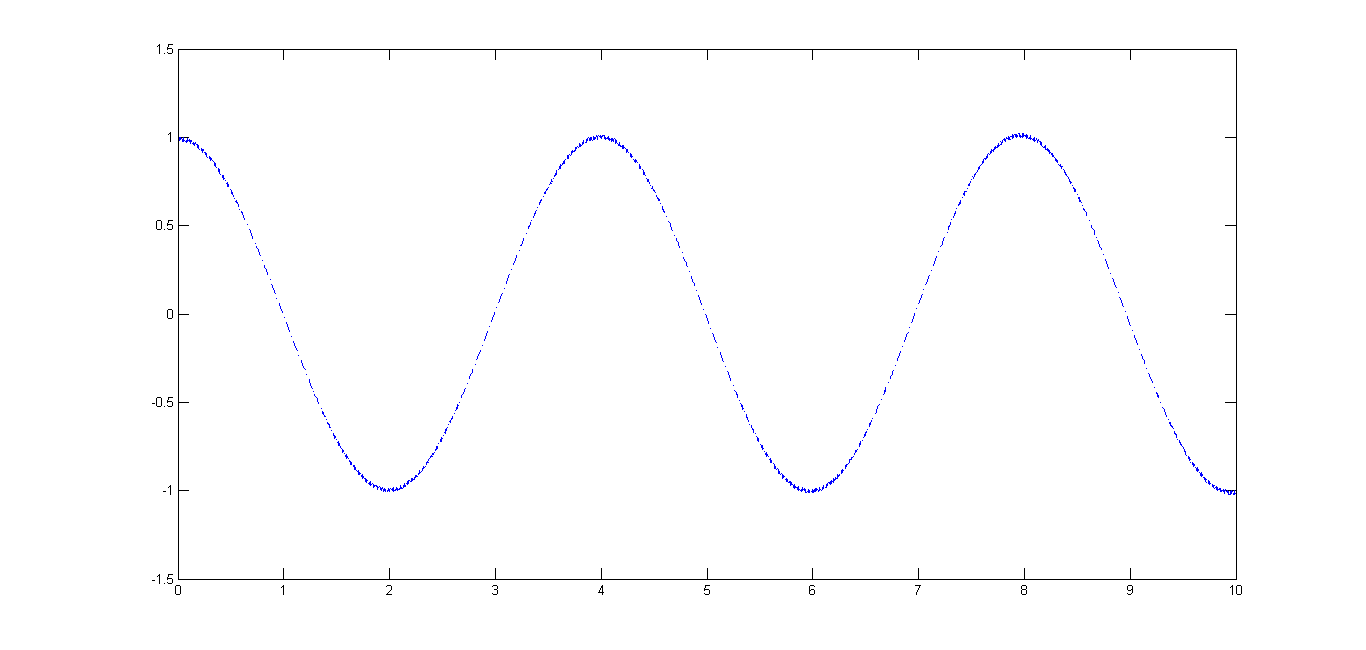
尽管我偏爱解析方法，但是数值分析发能够让我们先一瞧解的大概性质，以下是用Matlab求得的在$l=1,g=10,h=0.01,\omega=500$的情况下、初始条件为$\theta_0=1,\dot{\theta}_0=0$的解

在$l=1,g=10,h=0.01,\omega=500$的情况下的解，图像类似于简谐运动

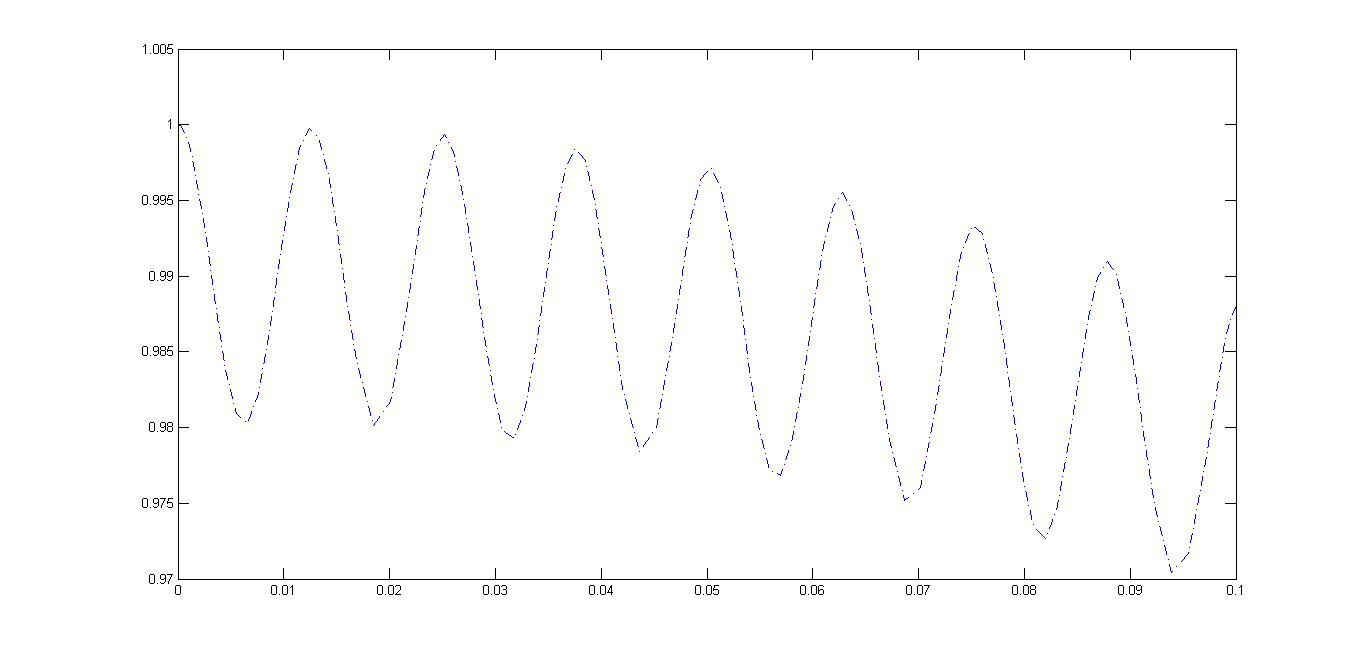
图像表明周期解还是比较理想的，有点像简谐运动的解了，事实上也正是如此。但我们来仔细观察局部情况

上图中的“简谐运动”实际上叠加了一个高频振荡。

不难发现实际上的运动是在简谐运动基础上叠加了一个高频振荡。这也就不难理解为什么解析方法求解此题会遇到很多困难，主要是高频函数的存在。比如$\sin\omega t$是一个非常理想的函数，但是如果展开为泰勒级数就成了$\omega t-\frac{\omega^3 t^3}{6}+\dots$，如果只取前几项，收敛区域是非常小的。

现在关键的问题是，既然已经初步观察到是由双频率叠加的，我们最好能够把这两个频率分离开来，分别研究。这就是本文的核心。

分离频率

为了分离频率，我构思了以下方程组
$$\left\{ \begin{array}{l}
{\ddot{\phi}_1+\Omega^2 \phi_1=\varepsilon\left[\Omega^2 \phi_1+g\left(\phi_1+\phi_2\right)-\left(h_0 \omega^2 \cos\omega t\right)\phi_2\right]}\\
{\ddot{\phi}_2+\omega^2 \phi_2=\varepsilon\left[\omega^2 \phi_2-\left(h_0 \omega^2 \cos\omega t\right)\phi_1\right]}
\end{array} \right.$$

将两道方程叠加起来，取$\varepsilon=1$就得到了原来的Mathieu方程，其中$\theta=\phi_1+\phi_2$，而$\Omega$是待定的。初始条件是$\phi_1(0)=\theta_0,\dot{\phi}_1(0)=0;\phi_2(0)=h_0 \theta_0,\dot{\phi}_2(0)=0$。这样就相当于求解原Mathieu方程在$\theta(0)=(1+h_0)\theta_0,\dot{\theta}(0)=0$下的解。

把$\varepsilon$看作小参数，先求$\phi_2$，略去含有$\varepsilon$的项，即
$$\ddot{\phi}_2+\omega^2 \phi_2=0$$
结合初始条件得到
$$\phi_2=\theta_0 h_0 \cos\omega t$$
同理，对$\phi_1$进行同样的处理，我们求得
$$\phi_1=\theta_0 \cos\Omega t$$

要检验此解的合理性，主要是看略去的项是否合理。对于$\phi_2$，我们略去了$\varepsilon\left[\omega^2 \phi_2-\left(h_0 \omega^2 \cos\omega t\right)\phi_1\right]$，将所求得的$\phi_1$和$\phi_2$代进去，有
$$\begin{aligned}
\varepsilon\left[\omega^2 \theta_0 h_0 \cos\omega t-\left(h_0 \omega^2 \cos\omega t\right)\theta_0 \cos\Omega t\right]\\
=\varepsilon\omega^2 \theta_0 h_0 \cos\omega t(1-\cos\Omega t)
\end{aligned}$$
其中$\cos\Omega t$是一个低频项，在开始的长时间内（相对于高频项的周期）它都近似为1（这可以简单总结为在低频项中高频取0，在高频项中低频取常值），因此这一整项可以近似看作零。这表明，我们的略去是“自洽”的

对于$\phi_1$，我们略去了$\varepsilon\left[\Omega^2 \phi_1+g\left(\phi_1+\phi_2\right)-\left(h_0 \omega^2 \cos\omega t\right)\phi_2\right]$，代入即得
$$\begin{aligned}
\varepsilon \left[\Omega^2 \theta_0 \cos\Omega t+g\left(\theta_0 \cos\Omega t+\theta_0 h_0 \cos\omega t\right)-\left(h_0 \omega^2 \cos\omega t\right)\theta_0 h_0 \cos\omega t\right]\\
=\varepsilon\left[(\Omega^2+g)\theta_0 \cos\Omega t-\frac{1}{2}\theta_0 h_0^2 \omega^2+g\theta_0 h_0 \cos\omega t -\frac{1}{2}\theta_0 h_0^2 \omega^2 \cos 2\omega t\right]
\end{aligned}$$
继续我们的“高频取0，低频取1”，就得到
$$\varepsilon\left[(\Omega^2+g)\theta_0 -\frac{1}{2}\theta_0 h_0^2 \omega^2\right]$$
为了让项的略去更合理，这一项应该要近似为0，因此
$$\Omega^2=\frac{1}{2} h_0^2 \omega^2-g\geq 0$$
我们在上面的计算中默认了$l=1$，一般地有
$$\Omega^2=\frac{1}{2} h_0^2 \omega^2-gl\geq 0$$
这和朗道的《力学》中求得的结果是一样的，也和范翔的结果一致，可谓殊途同归，异曲同工！

所以最终我们求得近似解为
$$\theta\approx \theta_0 \cos\Omega t+h_0 \theta_0 \cos\omega t$$
为了求更高精度的近似解，我们可以把上面的方程组继续对$\varepsilon$展开。由于过程过于繁琐，在此从略。

转载到请包括本文地址：https://kexue.fm/archives/2471

更详细的转载事宜请参考：《科学空间FAQ》