生成扩散模型漫谈（二十九）：用DDPM来离散编码

笔者前两天在arXiv刷到了一篇新论文《Compressed Image Generation with Denoising Diffusion Codebook Models》，实在为作者的天马行空所叹服，忍不住来跟大家分享一番。

如本文标题所述，作者提出了一个叫DDCM（Denoising Diffusion Codebook Models）的脑洞，它把DDPM的噪声采样限制在一个有限的集合上，然后就可以实现一些很奇妙的效果，比如像VQVAE一样将样本编码为离散的ID序列并重构回来。注意这些操作都是在预训练好的DDPM上进行的，无需额外的训练。

有限集合 #

由于DDCM只需要用到一个预训练好的DDPM模型来执行采样，所以这里我们就不重复介绍DDPM的模型细节了，对DDPM还不大了解的读者可以回顾我们《生成扩散模型漫谈》系列的（一）、（二）、（三）篇。

我们知道，DDPM的生成采样是从$\boldsymbol{x}_T\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$出发，由下式迭代到$\boldsymbol{x}_0$：
\begin{equation}\boldsymbol{x}_{t-1} = \boldsymbol{\mu}(\boldsymbol{x}_t) + \sigma_t \boldsymbol{\varepsilon}_t,\quad \boldsymbol{\varepsilon}_t\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{I})\label{eq:ddpm-g}\end{equation}
对于DDPM来说，每一步的迭代都需要采样一个噪声，加上$\boldsymbol{x}_T$本身也是采样的噪声，所以通过$T$步迭代生成$\boldsymbol{x}_0$的过程中，共传入了$T+1$个噪声向量，假设$\boldsymbol{x}_t\in\mathbb{R}^d$，那么DDPM的采样过程实际上是一个$\mathbb{R}^{d\times (T+1)}\mapsto \mathbb{R}^d$的映射。

DDCM的第一个奇思妙想是将噪声的采样空间换成有限集合（Codebook）：
\begin{equation}\boldsymbol{x}_{t-1} = \boldsymbol{\mu}(\boldsymbol{x}_t) + \sigma_t \boldsymbol{\varepsilon}_t,\quad \boldsymbol{\varepsilon}_t\sim\mathcal{C}_t\label{eq:ddcm-g}\end{equation}
以及$\boldsymbol{x}_T\sim \mathcal{C}_{T+1}$，其中$\mathcal{C}_t$是$K$个从$\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$预采样好的噪声集合。换句话说，采样之前就从$\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$采样好$K$个向量并固定不变，后面每次采样都从这$K$个向量中均匀采样。这样一来，生成过程变成了$\{1,2,\cdots,K\}^{T+1}\mapsto \mathbb{R}^d$的映射。

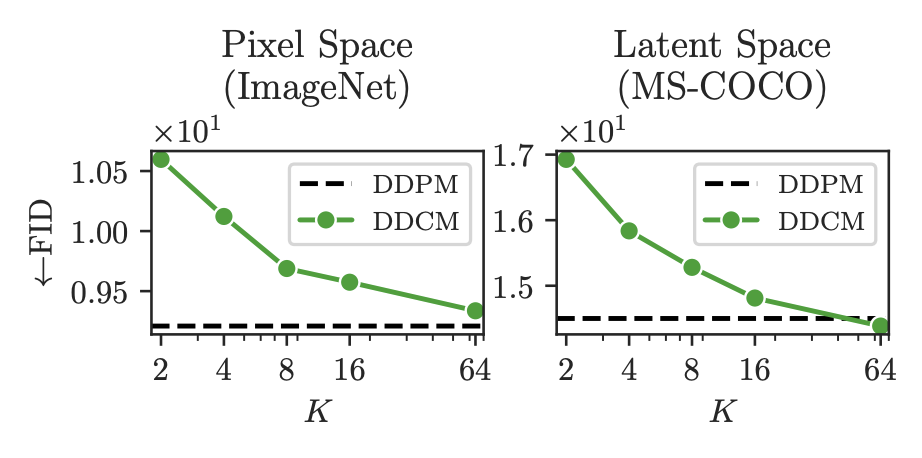
这样做对生成效果有什么损失呢？DDCM做了实验，发现损失很小：

可以看到，$K = 64$时已经基本追平FID，仔细观察就会发现其实$K=2$时也没损失多少，这表明采样空间有限化可以保持DDPM的生成能力。注意这里有个细节，每一步的$\mathcal{C}_t$是独立的，即所有Codebook加起来共有$(T+1)K$个噪声，而非共享$K$个噪声。笔者做了简单的复现，发现共享的话需要$K\geq 8192$才能保持相近效果。

离散编码 #

现在我们考虑一个逆问题：寻找给定$\boldsymbol{x}_0$的离散编码，即寻找相应的序列$\boldsymbol{\varepsilon}_T\in \mathcal{C}_T,\cdots,\boldsymbol{\varepsilon}_1\in \mathcal{C}_1$，使得迭代$\boldsymbol{x}_{t-1} = \boldsymbol{\mu}(\boldsymbol{x}_t) + \sigma_t \boldsymbol{\varepsilon}_t$生成的$\boldsymbol{x}_0$跟给定的样本尽可能接近。

既然将采样空间有限化后FID不会有明显变化，因此我们可以认为同分布的所有样本都可以通过式$\eqref{eq:ddcm-g}$来生成，所以上述逆问题的解理论上是存在的。可怎么把它找出来呢？直观的想法是从$\boldsymbol{x}_0$开始倒推，但细思之下我们会发现难以操作，比如第一步$\boldsymbol{x}_0 = \boldsymbol{\mu}(\boldsymbol{x}_1) + \sigma_1 \boldsymbol{\varepsilon}_1$，这里$\boldsymbol{x}_1$和$\boldsymbol{\varepsilon}_1$都是未知的，难以同时把它们定下来。

这时候DDCM的第二个奇思妙想登场了，它将$\boldsymbol{x}_0$的离散编码视为一个条件控制生成问题！具体来说，我们从固定的$\boldsymbol{x}_T$，通过如下方式来选择$\boldsymbol{\varepsilon}_t$：
\begin{equation}\boldsymbol{x}_{t-1} = \boldsymbol{\mu}(\boldsymbol{x}_t) + \sigma_t \boldsymbol{\varepsilon}_t,\quad \boldsymbol{\varepsilon}_t = \mathop{\text{argmax}}_{\boldsymbol{\varepsilon}\in\mathcal{C}_t} \boldsymbol{\varepsilon}\cdot(\boldsymbol{x}_0-\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t))\label{eq:ddcm-eg}\end{equation}
这里的$\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$是用$\boldsymbol{x}_t$来预测$\boldsymbol{x}_0$的模型，它跟$\boldsymbol{\mu}(\boldsymbol{x}_t)$的关系是：
\begin{equation}\boldsymbol{\mu}(\boldsymbol{x}_t) = \frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)\end{equation}
如果读者忘记了这部分内容，可以到《生成扩散模型漫谈（三）：DDPM = 贝叶斯 + 去噪》复习一下。

详细的推导我们下一节再讨论，现在先来观摩一下式$\eqref{eq:ddcm-eg}$，它跟随机生成的式$\eqref{eq:ddcm-g}$的唯一区别通过$\text{argmax}$来选择最优$\boldsymbol{\varepsilon}_t$，指标是$\boldsymbol{\varepsilon}$与残差$\boldsymbol{x}_0-\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$的内积相似度，直观理解就是让$\boldsymbol{\varepsilon}$尽可能补偿当前$\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$与目标$\boldsymbol{x}_0$的差距。通过迭代式$\eqref{eq:ddcm-eg}$，图片等价地被转化为$T-1$个整数（$\sigma_1$通常设为零）。

规则看上去很简单，那实际重构效果如何呢？下面截取了原论文的一个图，可以看到还是比较惊艳的，原论文还有更多效果图。笔者也在自己的模型尝试了一下，发现基本上能复现相近的效果，所以方法还是比较可靠的。

条件生成 #

刚才我们说了，DDCM将编码过程视为一个条件控制生成过程，怎么理解这句话呢？我们从DDPM的式$\eqref{eq:ddpm-g}$出发，它可以等价地写成
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) = \mathcal{N}(\boldsymbol{x}_{t-1};\boldsymbol{\mu}(\boldsymbol{x}_t),\sigma_t^2\boldsymbol{I})\end{equation}
现在我们要做的事情是已知$\boldsymbol{x}_0$的前提下调控生成过程，所以我们往上述分布中多加一个条件$\boldsymbol{x}_0$，即改为$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0)$。事实上在DDPM中，$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t,\boldsymbol{x}_0)$是有解析解的，我们在《生成扩散模型漫谈（三）：DDPM = 贝叶斯 + 去噪》已经求出过：
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \mathcal{N}\left(\boldsymbol{x}_{t-1};\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\boldsymbol{x}_0,\frac{\bar{\beta}_{t-1}^2\beta_t^2}{\bar{\beta}_t^2} \boldsymbol{I}\right)\end{equation}
或者写成
\begin{equation}\begin{aligned}
\boldsymbol{x}_{t-1} =&\, \frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\boldsymbol{x}_0 + \frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}\boldsymbol{\varepsilon}_t \\
=&\, \underbrace{\frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)}_{\boldsymbol{\mu}(\boldsymbol{x}_t)} + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}(\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) + \underbrace{\frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}}_{\sigma_t}\boldsymbol{\varepsilon}_t
\end{aligned}\label{eq:ddcm-eg0}\end{equation}
其中$\boldsymbol{\varepsilon}_t\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$。相比式$\eqref{eq:ddpm-g}$，上式多了$\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$一项，它用来引导生成结果向$\boldsymbol{x}_0$靠近。但别忘了我们的任务是离散编码$\boldsymbol{x}_0$，所以生成过程不能有$\boldsymbol{x}_0$显式参与，否则就因果倒置了。为此，我们寄望于$\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$这一项能从$\boldsymbol{\varepsilon}_t$中得到补偿，所以我们调整$\boldsymbol{\varepsilon}_t$的选择规则为
\begin{equation}\boldsymbol{\varepsilon}_t = \mathop{\text{argmin}}_{\boldsymbol{\varepsilon}\in\mathcal{C}_t} \left\Vert\frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}(\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) - \frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}\boldsymbol{\varepsilon}\right\Vert\label{eq:ddcm-eps0}\end{equation}
由于$\mathcal{C}_t$的向量都是从$\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$预采样好的，所以跟《让人惊叹的Johnson-Lindenstrauss引理：理论篇》里面的“单位模引理”类似，我们可以认为$\mathcal{C}_t$的向量模长大致相同，在这个假设之下，上式也等价于
\begin{equation}\boldsymbol{\varepsilon}_t = \mathop{\text{argmax}}_{\boldsymbol{\varepsilon}\in\mathcal{C}_t} \boldsymbol{\varepsilon}\cdot(\boldsymbol{x}_0-\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t))\end{equation}
这就得到了DDCM的式$\eqref{eq:ddcm-eg}$。

重要采样 #

在上述推导中，我们用到了“寄望于$\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)$这一项能从$\boldsymbol{\varepsilon}_t$中得到补偿，所以将$\boldsymbol{\varepsilon}_t$的选择规则改为式$\eqref{eq:ddcm-eps0}$”的说法，这样虽然看起来比较直观，但从数学上来说是不严谨的，甚至严格来说是错误的。这一节我们来将这部分内容严格化。

再次回顾式$\eqref{eq:ddcm-eg0}$，前面的推导直到式$\eqref{eq:ddcm-eg0}$都是严谨的，不严谨的地方在于建立将式$\eqref{eq:ddcm-eg0}$与$\mathcal{C}_t$联系起来的方式。试想一下，按照$\eqref{eq:ddcm-eps0}$来选$\boldsymbol{\varepsilon}_t$，当$K\to\infty$时会发生什么？此时我们可以认为$\mathcal{C}_t$已经覆盖了整个$\mathbb{R}^d$，所以$\frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}(\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) = \frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}\boldsymbol{\varepsilon}_t$，也就是说式$\eqref{eq:ddcm-eg0}$变成了确定性的变换：
\begin{equation}\boldsymbol{x}_{t-1} = \frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\bar{\boldsymbol{\mu}}(\boldsymbol{x}_t) + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}(\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)) = \frac{\alpha_t\bar{\beta}_{t-1}^2}{\bar{\beta}_t^2}\boldsymbol{x}_t + \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2}\boldsymbol{x}_0\end{equation}
换言之$K\to\infty$时无法恢复原本的随机采样轨迹，这其实并不是一件科学的事情。我们认为采样空间有限化应该是连续采样空间的一个近似，当$K\to\infty$时应该还原连续型的采样轨迹，这样离散化的每一步才更有理论保证，或者用一种更数学化的表达方式，就是我们认为必要条件是
\begin{equation}\lim_{K\to\infty} \text{DDCM} = \text{DDPM}\end{equation}

从式$\eqref{eq:ddpm-g}$变到式$\eqref{eq:ddcm-eg0}$，我们也可以认为是噪声分布从$\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$换成了$\mathcal{N}(\frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2\sigma_t}(\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)),\boldsymbol{I})$，但出于编码的需求，我们不能直接从后者采样，而只能从有限集合$\mathcal{C}_t$中采样。为了满足必要条件，即为了使采样结果更贴近从$\mathcal{N}(\frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2\sigma_t}(\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t)),\boldsymbol{I})$采样，我们可以用它的概率密度函数对$\boldsymbol{\varepsilon}\in\mathcal{C}_t$进行加权：
\begin{equation}p(\boldsymbol{\varepsilon})\propto \exp\left(-\frac{1}{2}\left\Vert\boldsymbol{\varepsilon} - \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2\sigma_t}(\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t))\right\Vert^2\right),\quad \boldsymbol{\varepsilon}\in\mathcal{C}_t\label{eq:ddcm-p}\end{equation}
也就是说，最合理的方式应该是对$-\frac{1}{2}\left\Vert\boldsymbol{\varepsilon} - \frac{\bar{\alpha}_{t-1}\beta_t^2}{\bar{\beta}_t^2\sigma_t}(\boldsymbol{x}_0 - \bar{\boldsymbol{\mu}}(\boldsymbol{x}_t))\right\Vert^2$做Softmax后按概率做重要性采样，而不是直接取$\text{argmax}$。只不过当$K$比较小时，Softmax之后的分布会接近one hot分布，所以按概率采样约等于$\text{argmax}$了。

一般形式 #

我们还可以将上述结果推广到Classifier-Guidance生成。根据《生成扩散模型漫谈（九）：条件控制生成结果》的推导，为式$\eqref{eq:ddpm-g}$加入Classifier-Guidance后的结果是
\begin{equation}\boldsymbol{x}_{t-1} = \boldsymbol{\mu}(\boldsymbol{x}_t) + \sigma_t^2 \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t) + \sigma_t\boldsymbol{\varepsilon}_t,\quad \boldsymbol{\varepsilon}_t\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})\end{equation}
即新增了$\sigma_t^2 \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)$，其中$p(\boldsymbol{y}|\boldsymbol{x}_t)$是带噪样本分类器，如果我们只有无噪样本分类器$p_o(\boldsymbol{y}|\boldsymbol{x})$，那么我们也可以让$p(\boldsymbol{y}|\boldsymbol{x}_t) = p_{o}(\boldsymbol{y}|\boldsymbol{\mu}(\boldsymbol{x}_t))$。

在同样的推导之下，我们可以得到类似式$\eqref{eq:ddcm-eps0}$的选择规则
\begin{equation}\boldsymbol{\varepsilon}_t = \mathop{\text{argmin}}_{\boldsymbol{\varepsilon}\in\mathcal{C}_t} \left\Vert\sigma_t^2 \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t) - \sigma_t\boldsymbol{\varepsilon}\right\Vert\end{equation}
或者近似地
\begin{equation}\boldsymbol{\varepsilon}_t = \mathop{\text{argmax}}_{\boldsymbol{\varepsilon}\in\mathcal{C}_t} \boldsymbol{\varepsilon}\cdot\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)\end{equation}
当然也可以按照式$\eqref{eq:ddcm-p}$来构造采样分布
\begin{equation}p(\boldsymbol{\varepsilon})\propto \exp\left(-\frac{1}{2}\left\Vert\boldsymbol{\varepsilon} - \sigma_t\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)\right\Vert^2\right),\quad \boldsymbol{\varepsilon}\in\mathcal{C}_t\end{equation}
这些都只是前述结果的简单推广。

个人评析 #

至此，我们对DDCM的介绍基本完毕，更多的细节大家请自行看原论文就好。作者还没有开源代码，这里笔者给出自己的参考实现：

DDCM：https://github.com/bojone/Keras-DDPM/blob/main/ddcm.py

如果大家对扩散模型已有一些了解并且手头上有现成的扩散模型，强烈推荐亲自试试。事实上DDCM的原理很好懂，代码也不难写，但只有亲自尝试过，才能体验到那种让人拍案叫绝的惊艳感。上一次给笔者相同感觉的是《生成扩散模型漫谈（二十三）：信噪比与大图生成（下）》介绍的一种免训练生成大图的技巧Upsample Guidance，同样体现了作者别出心裁的构思。

但从长远影响力来说，个人认为Upsample Guidance还是不如DDCM的。因为对图片做离散化编码是多模态LLM的主流路线之一，它充当着“图片Tokenizer”的角色，是相当关键的一环，而DDCM可以说是开辟了VQ、FSQ以外的全新路线，因此可能会有更深远的潜在影响。在原论文中，DDCM只将自己定义为Compression方法，反而有点“自视甚低”了。

作为一个离散编码模型，DDCM还有一个非常突出的优点是它出来的离散编码天然就是1D的，而不像VQ、FSQ等方案一样编码结果通常保留了图像的2D特性（TiTok等用了Q-Former思想去转1D的模型除外），这意味着我们在用这些编码做自回归生成时就不用再考虑“排序”这个问题了（参考《“闭门造车”之多模态思路浅谈（二）：自回归》），这一点会显得非常省心。

当然，目前看来它还有一些改进空间，比如目前的编码跟生成是同时进行的，这意味着DDPM的采样速度有多慢，DDCM的编码速度就有多慢，这在目前来说还是不大能接受的。偏偏我们还不能随便上加速采样的技巧，因为加速采样意味着减少了$T$，而减少$T$意味着缩短了编码长度，即增大了压缩率，那么会明显增加重构损失。

总的来说，个人认为DDCM是一种非常有意思的、潜力亟待挖掘、同时也亟待进一步优化的离散编码方法。

文章小结 #

本文介绍了扩散模型的一个新脑洞，它将DDPM生成过程中的噪声限制在一个有限的集合上，并结合条件生成的思路，将DDPM免训练地变成一个类似VQ-VAE的离散自编码器。

转载到请包括本文地址：https://kexue.fm/archives/10711

更详细的转载事宜请参考：《科学空间FAQ》