思考：两个椭圆片能粘合成一个立体吗？

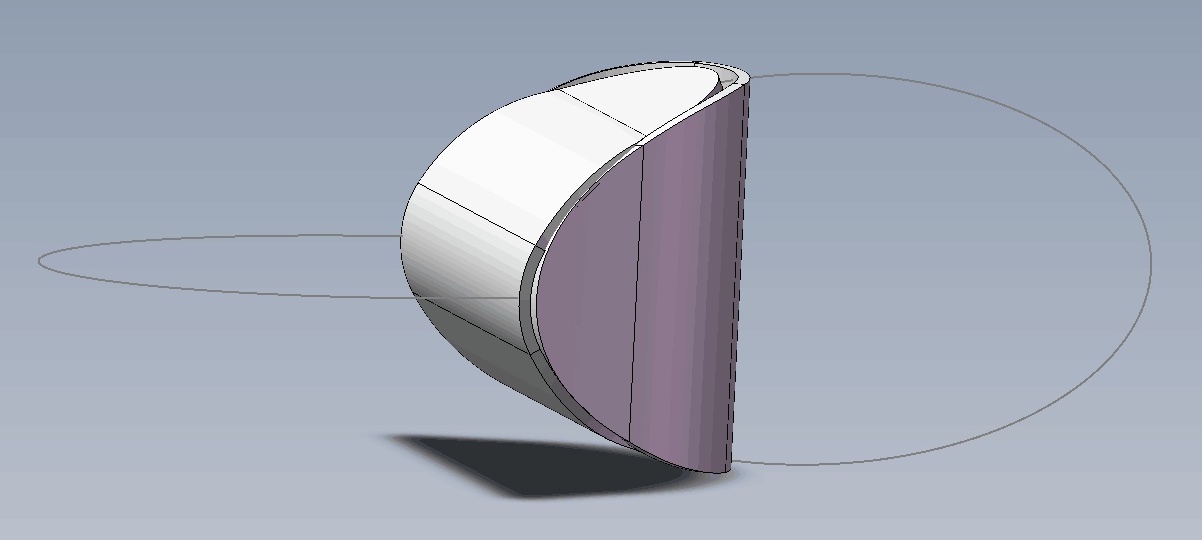
前两周又在群里看到一个颇为有趣的问题：两个同样大小的椭圆片可以沿着它们的长轴弯曲，沿着边缘线粘贴，能完美地贴合成一个封闭立体吗？问题来源于知乎《两个椭圆片可否以柱面弯曲边缘完美贴合？》。

问题可以用只言片语表达清楚，甚至普通读者都能理解，而问题本身是有一定难度的，这就符合了一个漂亮的问题的条件，所以也就吸引了笔者陆陆续续思考了好多天，最终在昨天算是给出了这类问题通用的列方程思路和数值求解方案，而今天则完成了理论证明，确认两个相同椭圆片总是可以完美贴合。

弧长参数方程 #

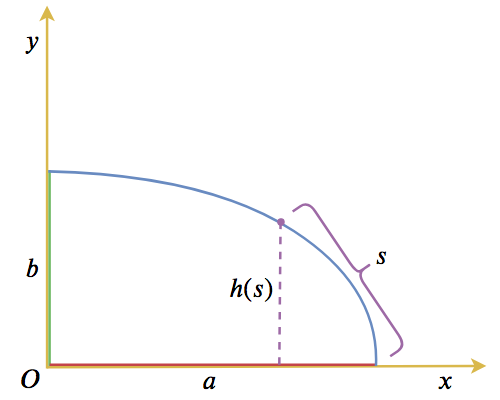
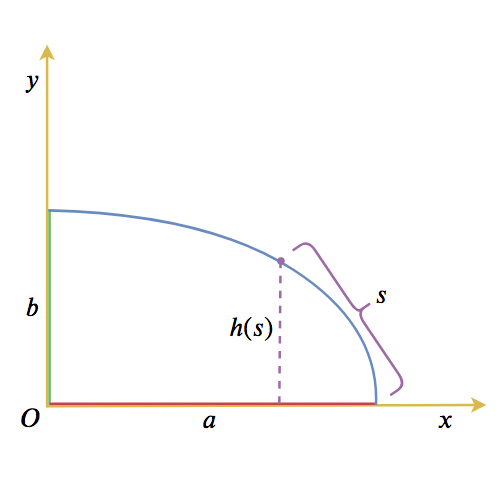
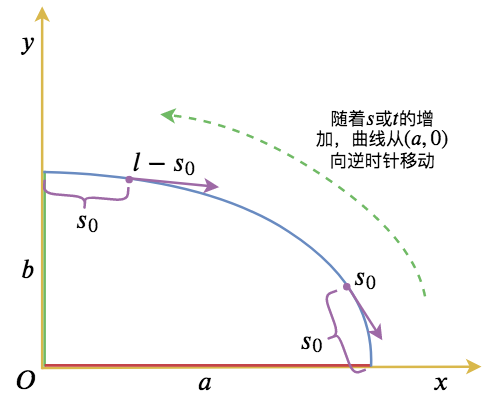
作为准备，我们先求出椭圆的弧长参数方程，如下图所示，当从$(a,0)$出发的一段椭圆弧长为$s$时，对应的$y=h(s)$是多少？

理论上，这个问题不难解决。因为椭圆的标准方程为：
\begin{equation}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\end{equation}
也就是$x=a\sqrt{1-y^2/b^2}$，这样椭圆弧长就可以表示为：
\begin{equation}s=\int_0^y \sqrt{1+\left(\frac{dx}{dy}\right)^2}dy=\int_0^y \sqrt{\frac{a^2 y^2}{b^4-b^2 y^2}+1}dy\label{eq:bs}\end{equation}
这个积分可以用“第二类不完全椭圆积分”来表示。在$[0,b]$区间内，$s$关于$b$是单调递增的，所以反函数必然存在。作为数值计算来说，我们不需要知道这个反函数是多少，我们只需要通过数值积分$\eqref{eq:bs}$算出一堆$(y,s)$的对应关系，将$y,s$交换位置，就相当于得到了关系$y=h(s)$（通过逐点法给出一个函数）。

粘贴边缘方程 #

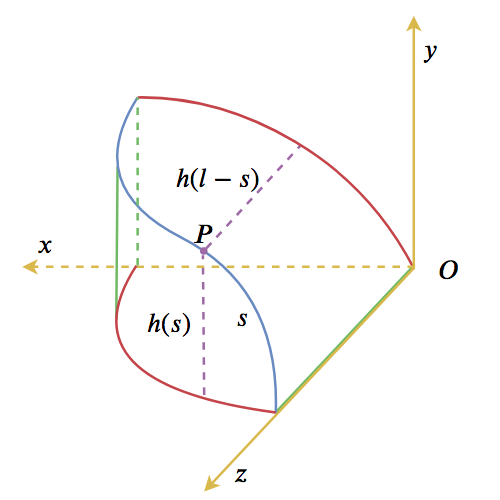
现在来看原始的问题：假设如果能粘合的情况下，边缘曲线方程是啥？我们按照下图（左图）所示来建立坐标系：

在上图中，只考虑第一卦限，蓝色线就是我们希望求参数方程的曲线，其中空间曲线与原来椭圆平面曲线的对应关系，已经用了跟前一图（右图）同一种颜色来表示。$P=(x(s),y(s),z(s))$为曲线上的一点，假设弧长$OP$为$s$，这段弧长实际上也就是椭圆上原来的一段弧长。而前面我们已经讨论过了，根据弧长可以求出$y$坐标
\begin{equation}y=h(s)\end{equation}
然后由于对称（互补）关系，$z$坐标事实上是弧长为$l-s$时对应的$y$坐标，即
\begin{equation}z=h(l-s)\end{equation}
其中$l$是整个椭圆周长的1/4，也就是蓝色曲线的总长度。

现在$y,z$都有了，还缺$x$，因为$s$是弧长参数，所以必然满足$dx^2+dy^2+dz^2=ds^2$，即
\begin{equation}\left(\frac{dx(s)}{ds}\right)^2+\left(\frac{dh(s)}{ds}\right)^2+\left(\frac{dh(l-s)}{ds}\right)^2=1\end{equation}
这样就可以把$x(s)$积分出来：
\begin{equation}x(s) = \int_0^s \sqrt{1-\left(\frac{dh(s)}{ds}\right)^2-\left(\frac{dh(l-s)}{ds}\right)^2}ds\label{eq:f}\end{equation}
而
\begin{equation}1-\left(\frac{dh(s)}{ds}\right)^2-\left(\frac{dh(l-s)}{ds}\right)^2 \geq 0\label{eq:c}\end{equation}
是否恒成立，就是是否能粘合的判别条件。

证明可以粘合 #

下面我们从理论上证明：两个椭圆片是可以完美贴合的，也就是验证$\eqref{eq:c}$恒成立。

首先，我们需要证明一个引理：

在椭圆$x^2/a^2 + y^2/b^2=1(a \geq b > 0)$中有
\begin{equation}\left.\left(\frac{dy}{dx}\right)^2\right|_{s=s_0}\leq \left.\left(\frac{dx}{dy}\right)^2\right|_{s=l-s_0}\end{equation}
也就是弧长为$s_0$处的斜率绝对值，不超过弧长为$l-s_0$处的斜率倒数的绝对值。

证明过程如下（并不难，手动画图，比划一下就明白了）：

利用椭圆常见的参数方程
\begin{equation}x=a\cos t,\quad y=b\sin t\end{equation}
注意这个参数$t$增加的方向，跟$s$增加的方向是是一样的，都是从$(a,0)$出发逆时针方向，因此$s$与$t$也是单调递增关系。

直观上看，就是要证明“侧看左边的箭头”要比“正看右边的箭头”更倾斜（更陡）

可以得到
\begin{equation}\left.\left(\frac{dy}{dx}\right)^2\right|_{t=t_0} = \frac{b^2\cos^2 t_0}{a^2\sin^2 t_0}\leq \frac{a^2\sin^2 (\pi/2-t_0)}{b^2\cos^2 (\pi/2-t_0)}=\left.\left(\frac{dx}{dy}\right)^2\right|_{t=\pi/2-t_0}\end{equation}
也就是说，$t=t_0$处的斜率，肯定不超过$t=\pi/2-t_0$处的斜率倒数的绝对值，并且很显然，$t_0$越小时$\left.\left(\frac{dx}{dy}\right)^2\right|_{t=\pi/2-t_0}$越大。

然后我们考虑
\begin{equation}\frac{ds}{dt}=\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}=dt\sqrt{a^2 - (a^2-b^2)\cos^2 t}\end{equation}
注意，这是一个$t$的单调递增函数（都只考虑$t\in[0,\pi/2]$区间），这意味着$s$随着$t$的增加而增加，并且增加的速度也越来越快，这意味着
\begin{equation}s_{[0,t_0]}\leq s_{[\pi/2-t_0,\pi/2]}\end{equation}
也就是说$[0,t_0]$区间的弧长，不超过$[\pi/2-t_0,\pi/2]$区间的弧长，这又意味着如果$s_{[0,t_0]} = s_{[\pi/2-t_1,\pi/2]}$，则$t_1 \leq t_0$。换言之，如果$s=s_0$对应$t=t_0$、$s=l-s_0$对应$t=t_1$的话，则$t_1 \leq t_0$，根据刚才的讨论：
\begin{equation}\left.\left(\frac{dy}{dx}\right)^2\right|_{s=s_0}=\left.\left(\frac{dy}{dx}\right)^2\right|_{t=t_0} \leq \left.\left(\frac{dx}{dy}\right)^2\right|_{t=\pi/2-t_1}=\left.\left(\frac{dx}{dy}\right)^2\right|_{s=l-s_0}\end{equation}

有了这个引理之后，我们去证明：
\begin{equation}\left(\frac{dh(s)}{ds}\right)^2+\left(\frac{dh(l-s)}{ds}\right)^2\leq 1\end{equation}
这里$h(s)$本来就是原来椭圆的$y$坐标，那么假设对应的$x$坐标为$g(s)$，则：
\begin{equation}\left(\frac{dh(s)}{ds}\right)^2+\left(\frac{dg(s)}{ds}\right)^2 = 1\end{equation}
那么等价于证明
\begin{equation}\left(\frac{dh(l-s)}{ds}\right)^2\leq\left(\frac{dg(s)}{ds}\right)^2\end{equation}
两边取倒数，然后利用$ds^2=dg^2+dh^2$，事实上就是要证明
\begin{equation}\left.\left(\frac{dg}{dh}\right)^2\right|_{s=l-s_0}\geq\left.\left(\frac{dh}{dg}\right)^2\right|_{s=s_0}\end{equation}
这就是刚才的引理。

数值求解结果 #

从数学上来看，$\eqref{eq:f}$已经称得上所求曲线的显式解（解析解）了，当然显式解不意味着是初等函数解，也不意味着这样的解答容易算。虽然微分几何中大多数结果都是以弧长为参数的方程，但那都是理论上的，事实上除了圆和直线，就没几条曲线的弧长参数方程是简单的。

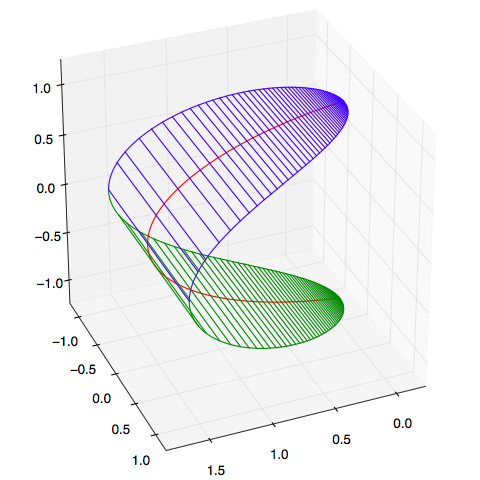
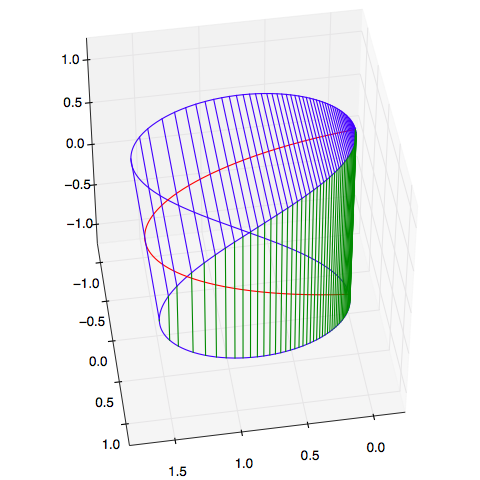
为了数值验证条件$\eqref{eq:c}$以及求解$\eqref{eq:f}$，我发现现成的数学软件（如Mathematica）并不好用，（对于笔者来说）最简单的方法还是直接通过Python写一段代码来模拟求解。以$a=2,b=1$为例，它通过了$\eqref{eq:c}$的数值验证，并且得到如下的解：

代码如下：

#! -*- coding: utf-8 -*-

import numpy as np


a = 2
b = 1
h = 1e-6 # 步长


def Int(y, x):
    """自定义数值积分函数
    """
    assert len(y) == len(x)
    dx = np.diff(x)
    _x = (x[:-1] + x[1:]) / 2
    _y = (y[:-1] + y[1:]) / 2
    s = np.cumsum(_y * dx)
    s = np.interp(x, _x, s, left=0)
    return s, x


def D(y, x):
    """自定义数值微分函数
    """
    assert len(y) == len(x)
    dy = np.diff(y) + 1e-10
    dx = np.diff(x) + 1e-10
    dy_dx = dy / dx
    _x = (x[:-1] + x[1:]) / 2
    dy_dx = np.interp(x, _x, dy_dx)
    return dy_dx, x


def s2y():
    """弧长到椭圆y轴的映射（即h(s)。）
    """
    y = np.arange(0, b, h)
    ds = np.sqrt(1 + a**2 * y**2 / b**2 / (b**2 - y**2))
    return Int(ds, y)[::-1]


y, s = s2y()
l = s[-1]
z = np.interp(l - s, s, y)
dx2 = 1 - D(y, s)[0]**2 - D(z, s)[0]**2
assert (dx2 > - 10 * h).all() # 判断是否能粘合，即在10倍步长的误差内是否恒大于等于0
dx = np.sqrt(np.clip(dx2, 0, a))
x = Int(dx, s)[0]


# 采样1/10的点去绘图
x = x[::10]
y = y[::10]
z = z[::10]


from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt


plt.clf()
fig = plt.figure(figsize=(8, 8))
ax = fig.gca(projection='3d')
ax.plot(x, y, z, color='blue')
ax.plot(x, - y, z, color='blue')
ax.plot(x, y, - z, color='green')
ax.plot(x, - y, - z, color='green')
ax.plot(x, np.zeros_like(x), z, color='red')
ax.plot(x, np.zeros_like(x), - z, color='red')


for i in range(0, len(x), 2000):
    _ = ax.plot([x[i], x[i]], [y[i], - y[i]], [z[i], z[i]], color='blue')
    _ = ax.plot([x[i], x[i]], [y[i], - y[i]], [- z[i], - z[i]], color='green')

for i in [-1, -1000]:
    _ = ax.plot([x[i], x[i]], [y[i], - y[i]], [z[i], z[i]], color='blue')
    if i != -1:
        _ = ax.plot([x[i], x[i]], [y[i], - y[i]], [- z[i], - z[i]], color='green')


ax.set_xlim(0, a)
ax.set_ylim(-b * 1.2, b * 1.2)
ax.set_zlim(-b * 1.2, b * 1.2)

plt.show()

小结 #

本文分析了两个椭圆片的粘合问题，其核心思想是用弧长参数化曲线方程，虽然文章是以椭圆为例，但显然可以推广到一般的两个平面曲线面的弯曲粘合问题，只需要分别求出各自的弧长参数方程（即$h(l-s)$换成另一条曲线的弧长参数化方程），然后沿用$\eqref{eq:f}$式积分。

总算基本解决了一个比较有意思的问题，来证明自己的数学兴趣和能力还在～

转载到请包括本文地址：https://kexue.fm/archives/6818

更详细的转载事宜请参考：《科学空间FAQ》