ARXIV数学论文分布:偏微分方程最热门!
By 苏剑林 | 2015-11-13 | 40262位读者 |笔者成功地保研到了中山大学的基础数学专业,这个专业自然是比较理论性的,虽然如此,我还会保持着我对数据分析、计算机等方面的兴趣。这几天兴致来了,想做一下结合我的专业跟数据挖掘相结合的研究,所以就爬取了ARXIV上面近五年(2010年到2014年)的数学论文(包含的数据有:标题、分类、年份、月份),想对这几年来数学的“行情”做一下简单的分析。个人认为,ARVIX作为目前全球最大的论文预印本的电子数据库,对它的数据进行分析,所得到的结论是能够具有一定的代表性的。
当然,本文只是用来练手爬虫和基本数据分析的文章,并没有挖掘出特别有价值的信息。文末附录了笔者爬取到的数据,供有兴趣的读者进一步分析研究。
整体情况 #
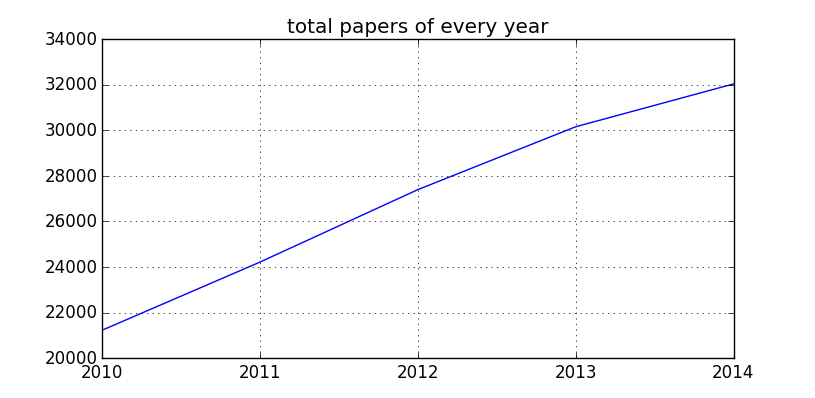
这五年来,ARXIV的数学论文总数为135009篇,平均每年27000篇,或者每天74篇。
就分类来看,文章数排名前十五的分类是:
| 分类 | 文章数 |
| Analysis of PDEs (math.AP) | 9417 |
| Probability (math.PR) | 9064 |
| Combinatorics (math.CO) | 8937 |
| Mathematical Physics (math-ph) | 8852 |
| Information Theory (cs.IT) | 8215 |
| Algebraic Geometry (math.AG) | 7524 |
| Number Theory (math.NT) | 6789 |
| Differential Geometry (math.DG) | 6495 |
| Dynamical Systems (math.DS) | 4834 |
| Functional Analysis (math.FA) | 4375 |
| Numerical Analysis (math.NA) | 4058 |
| Optimization and Control (math.OC) | 4015 |
| Classical Analysis and ODEs (math.CA) | 3511 |
| Representation Theory (math.RT) | 3431 |
| Geometric Topology (math.GT) | 3256 |
这个表某种意义上代表了数学各个方向的热门程度。首先排名第一的是偏微分方程,它跟第四的数学物理多少有点联系,两者基本都代表了偏微分方程的应用,尤其是它在物理、生物等各种领域的应用。排名第二的是概率论,由于我们的世界中几乎任意现象都带有随机性,自然也带动了这个方向的发展,因此概率论的热门也是合乎常理的。第三是组合数学,它是离散数学的代表。第五是信息理论,它应该是最近几年数据挖掘发展的结果。后面是代数几何、数论、微分几何、动力学系统、泛函分析、数值分析、最优化控制等,这些应该都是数学中比较前沿和热门的领域。
然后,我把标题分拆,看看哪些词在标题上出现最多。结果很容易想到,最多的是of,and,the,for,in,with,a,on这些没什么特别意义的停用词,把这些停用词去掉之后,得到的结果是:
equations(5172), groups(4782), spaces(4531), systems(4422), random(3980), functions(3906), quantum(3817), equation(3720), algebras(3686), theory(3459), graphs(3437), problem(3337), finite(3275), model(3216), solutions(3097), theorem(3014), operators(2880), linear(2718), generalized(2622), type(2579), group(2565), space(2402), manifolds(2363), analysis(2315), stochastic(2278), problems(2235), models(2161), surfaces(2156), applications(2060), nonlinear(2017), approach(1961), local(1930), polynomials(1922), method(1919), fields(1886), differential(1882), new(1874), optimal(1869), function(1854), boundary(1789), number(1768), sets(1766), curves(1751)
第一个equations,和第八个equation,估计就对应着分类中的偏微分方程,而且接着是groups(群论), spaces(空间)等,估计是代表了目前数学研究的主流方法,即把研究对象放到某个空间之中,结合泛函分析和抽象代数(尤其是群论)进行研究。有意思的是,quantum(量子)一词也排在前面,这应该表明了以量子理论为背景数学研究也如火如荼。其他方面读者可以自己评价。
逐年变化 #
看完了整体情况,我们可以来看逐年变化,首先逐年文章变化,每年的文章数都在增加:
然后,我们来看五年来,文章数目最多的五个类别,看看哪些领域在逐步变得热门起来。
2010 数学物理(1619) 概率论(1437) 代数几何(1358) PDEs分析(1319) 组合数学(1297)
2011 数学物理(1809) 概率论(1671) 组合数学(1605) PDEs分析(1545) 代数几何(1414)
2012 数学物理(2005) PDEs分析(1319) 组合数学(1826) 概率论(1824) 信息理论(1616)
2013 PDEs分析(2211) 概率论(2027) 组合数学(2020) 信息理论(1958) 数学物理(1773)
2014 PDEs分析(2464) 组合数学(2189) 概率论(2105) 信息理论(2008) 数学物理(1646)
可以看到,前三年数学物理这一方向的论文数稳居第一,而后两年,在论文总数增加的情况下,数学物理的论文数却有着较大幅度的下降,这似乎表明在数学物理方向似乎遇到了瓶颈?而相反,逐年增加并且慢慢提升到第一位的是PDEs分析,这表明偏微分方程组的研究一直是当代数学研究的主流领域。
看看哪些类别增速最快?下面挑了一下笔者认为比较具有代表性的。
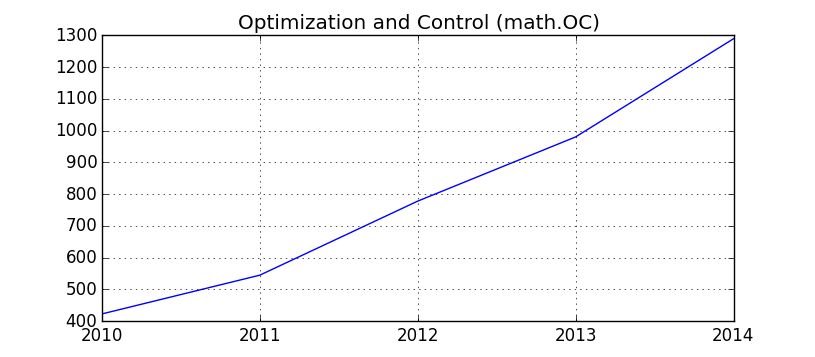
第一个是Systems and Control (cs.SY),系统与控制,这五年的论文数依次为9,96,112,139,135;跟这个有点相关的,是Optimization and Control (math.OC),最优化与控制,五年的论文数依次为423,545,778,980,1289
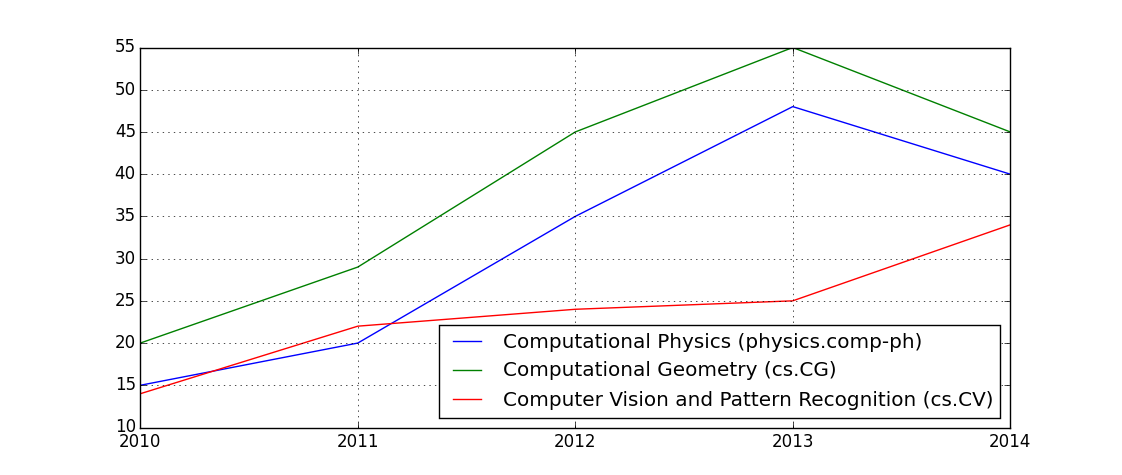
此外,数值分析也越来越热门,它的论文数逐年增加,增幅算是比较大的,五年的论文数依次为435,571,778,1012,1262。这些条件表明,数学与计算机的结合是数学发展的主流趋势之一。能反映这个趋势的类别还有Computational Physics (physics.comp-ph)、Computational Geometry (cs.CG)、Computer Vision and Pattern Recognition (cs.CV)等。
笔者简单使用了一个指标来衡量一个分类的增幅速度:
$$\sum_{n=2010}^{2013}\frac{(n+1)\text{年的论文数}}{n\text{年的论文数}}$$
首先声明,这个指标非常简单,而且不一定准确,仅作感性认知所用,由此指标所筛选出来的增幅速度最大的分类依次如下表。有意思的是,其中不少领域都跟计算机有些联系,我认为,这不是一个巧合。
| 2010 | 2011 | 2012 | 2013 | 2014 | |
| Earth and Planetary Astrophysics (astro-ph.EP) | 1 | 11 | 12 | 3 | 7 |
| Systems and Control (cs.SY) | 9 | 96 | 112 | 139 | 135 |
| Other Condensed Matter (cond-mat.other) | 8 | 3 | 8 | 1 | 7 |
| Databases (cs.DB) | 1 | 6 | 5 | 1 | 2 |
| Other Statistics (stat.OT) | 1 | 6 | 4 | 4 | 5 |
| Cellular Automata and Lattice Gases (nlin.CG) | 5 | 1 | 8 | 3 | 1 |
| Computation and Language (cs.CL) | 3 | 3 | 1 | 4 | 14 |
| History and Philosophy of Physics (physics.hist-ph) | 6 | 9 | 1 | 4 | 12 |
| Social and Information Networks (cs.SI) | 4 | 11 | 19 | 21 | 15 |
| Neural and Evolutionary Computing (cs.NE) | 5 | 6 | 4 | 15 | 9 |
| Cell Behavior (q-bio.CB) | 2 | 6 | 3 | 2 | 4 |
| Software Engineering (cs.SE) | 1 | 3 | 4 | 4 | 2 |
| Networking and Internet Architecture (cs.NI) | 29 | 44 | 56 | 76 | 118 |
| Physics and Society (physics.soc-ph) | 5 | 11 | 15 | 15 | 15 |
| Chemical Physics (physics.chem-ph) | 7 | 8 | 4 | 13 | 8 |
| High Energy Physics - Lattice (hep-lat) | 3 | 7 | 11 | 9 | 7 |
| Discrete Mathematics (cs.DM) | 54 | 88 | 125 | 187 | 152 |
| Machine Learning (stat.ML) | 30 | 43 | 60 | 86 | 91 |
| Optimization and Control (math.OC) | 423 | 545 | 778 | 980 | 1289 |
| Computational Physics (physics.comp-ph) | 15 | 20 | 35 | 48 | 40 |
| Data Structures and Algorithms (cs.DS) | 35 | 50 | 81 | 90 | 99 |
| Numerical Analysis (math.NA) | 435 | 571 | 778 | 1012 | 1262 |
| Cryptography and Security (cs.CR) | 21 | 37 | 35 | 66 | 40 |
| Numerical Analysis (cs.NA) | 26 | 26 | 47 | 44 | 61 |
| Quantitative Methods (q-bio.QM) | 7 | 14 | 15 | 8 | 12 |
| Adaptation and Self-Organizing Systems (nlin.AO) | 9 | 13 | 23 | 15 | 18 |
| Computer Vision and Pattern Recognition (cs.CV) | 14 | 22 | 24 | 25 | 34 |
| Computational Geometry (cs.CG) | 20 | 29 | 45 | 55 | 45 |
| Solar and Stellar Astrophysics (astro-ph.SR) | 2 | 6 | 6 | 5 | 1 |
| Artificial Intelligence (cs.AI) | 8 | 13 | 22 | 15 | 15 |
附件下载 #
最后,放上我爬取到的文件,有兴趣的读者可以进一步拿来分析。
arxiv.zip
转载到请包括本文地址:https://kexue.fm/archives/3511
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Nov. 13, 2015). 《ARXIV数学论文分布:偏微分方程最热门! 》[Blog post]. Retrieved from https://kexue.fm/archives/3511
@online{kexuefm-3511,
title={ARXIV数学论文分布:偏微分方程最热门!},
author={苏剑林},
year={2015},
month={Nov},
url={\url{https://kexue.fm/archives/3511}},
}












May 26th, 2018
苏先生,感觉这个很有用。请问能否分享一下代码。因为看论文,可以分析一下这个领域的研究进展。谢谢。
不好意思,好久之前的文章了,源码并没有保留~参照着流程实现吧,不算复杂。