生成扩散模型漫谈（十）：统一扩散模型（理论篇）

老读者也许会发现，相比之前的更新频率，这篇文章可谓是“姗姗来迟”，因为这篇文章“想得太多”了。

通过前面九篇文章，我们已经对生成扩散模型做了一个相对全面的介绍。虽然理论内容很多，但我们可以发现，前面介绍的扩散模型处理的都是连续型对象，并且都是基于正态噪声来构建前向过程。而“想得太多”的本文，则希望能够构建一个能突破以上限制的扩散模型统一框架（Unified Diffusion Model，UDM）：

1、不限对象类型（可以是连续型$\boldsymbol{x}$，也可以是离散型的$\boldsymbol{x}$）；

2、不限前向过程（可以用加噪、模糊、遮掩、删减等各种变换构建前向过程）；

3、不限时间类型（可以是离散型的$t$，也可以是连续型的$t$）；

4、包含已有结果（可以推出前面的DDPM、DDIM、SDE、ODE等结果）。

这是不是太过“异想天开”了？有没有那么理想的框架？本文就来尝试一下。

前向过程 #

从前面的一系列介绍中，我们知道构建一个扩散模型包含“前向过程”、“反向过程”、“训练目标”三个部分，这一节我们来分析“前向过程”。

在最初的DDPM中，我们是通过$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$来描述前向过程的；后来，随着DDIM等工作的发表，我们逐渐意识到，扩散模型的训练目标和生成过程，都跟$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$没直接联系，反而跟$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$的联系更为直接，而从$p(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$推导$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$往往也比较困难。因此，一个更为实用的操作就是直接以$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$为出发点，也就是将$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$视为前向过程。

$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$的最直接作用，就是用来构建扩散模型的训练数据，因此$p(\boldsymbol{x}_t|\boldsymbol{x}_0)$的最基本要求是便于采样。为此，我们可以通过重参数
\begin{equation}\boldsymbol{x}_t = \boldsymbol{\mathcal{F}}_t(\boldsymbol{x}_0,\boldsymbol{\varepsilon})\label{eq:re-param}\end{equation}
其中$\boldsymbol{\mathcal{F}}$是关于$t,\boldsymbol{x}_0,\boldsymbol{\varepsilon}$的确定性函数，$\boldsymbol{\varepsilon}$是采样自某个标准分布$q(\boldsymbol{\varepsilon})$的随机变量，常见选择是标准正态分布，但其他分布通常也是可行的。可以想像，该形式包含了足够丰富的$\boldsymbol{x}_0$到$\boldsymbol{x}_t$的变换，它对$\boldsymbol{x}_0$、$\boldsymbol{x}_t$的数据类型也没有约束。一般情况下，唯一的限制是$t$越小，$\boldsymbol{\mathcal{F}}_t(\boldsymbol{x}_0,\boldsymbol{\varepsilon})$所包含的$\boldsymbol{x}_0$的信息越完整，换言之用$\boldsymbol{\mathcal{F}}_t(\boldsymbol{x}_0,\boldsymbol{\varepsilon})$重构$\boldsymbol{x}_0$越容易，反之$t$越大重构就越困难，直到某个上界$T$时，$\boldsymbol{\mathcal{F}}_T(\boldsymbol{x}_0,\boldsymbol{\varepsilon})$所包含的$\boldsymbol{x}_0$的信息几乎消失，重构几乎不能完成。

反向过程 #

扩散模型的反向过程是通过多步迭代来逐渐生成逼真的数据，其关键就是概率分布$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$。一般地，我们有
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) = \int p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) p(\boldsymbol{x}_0|\boldsymbol{x}_t) d\boldsymbol{x}_0\label{eq:p-factor}\end{equation}
如果$\boldsymbol{x}_0$是离散型数据，将积分改为求和即可。$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$的基本要求也是便于采样，所以我们要求$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$和$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$也要便于采样，这样一来，我们就可以通过下述流程完成$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$的采样：
\begin{equation}\hat{\boldsymbol{x}}_0\sim p(\boldsymbol{x}_0|\boldsymbol{x}_t)\quad \& \quad \boldsymbol{x}_{t-1}\sim p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0=\hat{\boldsymbol{x}}_0) \quad \Rightarrow \quad \boldsymbol{x}_{t-1}\sim p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)\end{equation}
从这个分解来看，每一步$\boldsymbol{x}_t\to \boldsymbol{x}_{t-1}$的采样，实际上包含了两个子步骤：

1、预估：由$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$对$\boldsymbol{x}_0$做一个简单的“预估”；

2、修正：由$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$整合预估结果，将估值推前一小步。

所以，扩散模型的反向过程就是一个反复的“预估-修正”过程，通过不断地整合$\boldsymbol{x}_t\to \boldsymbol{x}_0$的预估结果，得到逐步推进的修正序列$\boldsymbol{x}_T\to\cdots\to\boldsymbol{x}_t\to \boldsymbol{x}_{t-1}\to\cdots\to \boldsymbol{x}_0$，将原本难以一步到位的生成分解为了多个步骤来完成。

训练目标 #

当然，目前的反向过程还只是“纸上谈兵”，因为对于$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$和$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$我们还一无所知。这一节我们先来讨论$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$。

很明显，$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$就是用$\boldsymbol{x}_t$来预测$\boldsymbol{x}_0$的概率模型，我们需要用一个“方便采样且容易计算”的分布去估计它。当$\boldsymbol{x}_0$是连续型数据时，我们的选择并不多，通常就是均值可训练的正态分布
\begin{equation}p(\boldsymbol{x}_0|\boldsymbol{x}_t) \approx q(\boldsymbol{x}_0|\boldsymbol{x}_t) = \mathcal{N}(\boldsymbol{x}_0;\boldsymbol{\mathcal{G}}_t(\boldsymbol{x}_t),\bar{\sigma}_t^2 \boldsymbol{I})\label{eq:normal}\end{equation}
为了降低训练难度，我们一般不将方差$\bar{\sigma}_t^2$视为可训练参数，而是用《生成扩散模型漫谈（七）：最优扩散方差估计（上）》的方式去事后估计它。另一方面，当$\boldsymbol{x}_0$是离散型数据时，我们可以用自回归或者非自回归的语言模型（Seq2Seq）来建模，离散型的概率建模和采样相对来说都更加容易些。

有了近似分布$q(\boldsymbol{x}_0|\boldsymbol{x}_t)$的具体形式后，训练目标就很简单了，比较自然的选择是交叉熵：
\begin{equation}\mathbb{E}_{\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0),\boldsymbol{x}_t\sim p(\boldsymbol{x}_t|\boldsymbol{x}_0)}[-\log q(\boldsymbol{x}_0|\boldsymbol{x}_t)] = \mathbb{E}_{\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0),\boldsymbol{\varepsilon}\sim q(\boldsymbol{\varepsilon})}[-\log q(\boldsymbol{x}_0|\boldsymbol{\mathcal{F}}_t(\boldsymbol{x}_0,\boldsymbol{\varepsilon}))]\end{equation}
这就解决了$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$的估计和训练目标的设计问题。如果$q(\boldsymbol{x}_0|\boldsymbol{x}_t)$是式$\eqref{eq:normal}$的标准正态分布，那么省去常数后的结果就是
\begin{equation}\mathbb{E}_{\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0),\boldsymbol{\varepsilon}\sim q(\boldsymbol{\varepsilon})}\left[\frac{1}{2\bar{\sigma}_t^2}\Vert\boldsymbol{x}_0 - \boldsymbol{\mathcal{G}}_t(\boldsymbol{\mathcal{F}}_t(\boldsymbol{x}_0,\boldsymbol{\varepsilon}))\Vert^2\right]\end{equation}

条件概率 #

现在就剩下$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$了，它是给定$\boldsymbol{x}_t, \boldsymbol{x}_0$来预测$\boldsymbol{x}_{t-1}$的概率。这个概率分布也有一定的设计空间，但前提是满足边缘分布的恒等式
\begin{equation}\int p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)p(\boldsymbol{x}_t|\boldsymbol{x}_0) d\boldsymbol{x}_t= p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)\label{eq:margin}\end{equation}
很显然，满足这个等式的一个最简单选择是直接取
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)\end{equation}
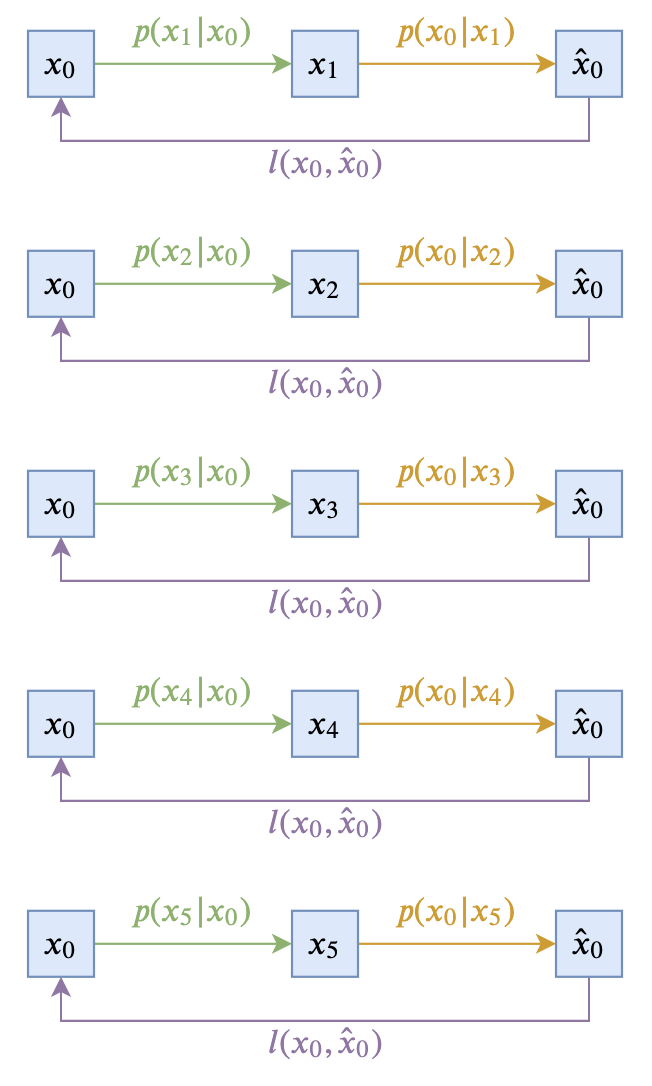
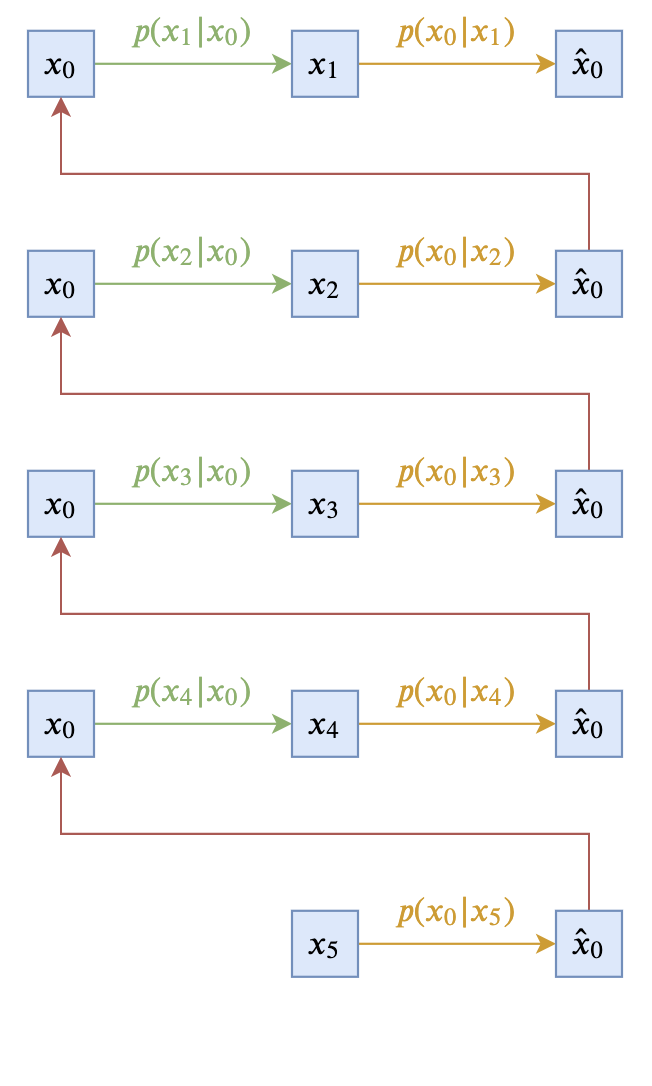
即让$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$跟$\boldsymbol{x}_t$无关。这样的扩散模型，可以由下面两个图描述（以$T=5$为例）：

这个极简的选择在理论上没有问题，然而实际上的效果通常不会太好，因此此时$\boldsymbol{x}_{t-1}$完全依赖于$\boldsymbol{x}_0$，而$\boldsymbol{x}_0$本来代表的是原始真实样本，在反向过程中我们则只能通过近似分布$q(\boldsymbol{x}_0|\boldsymbol{x}_t)$来近似采样，而$q(\boldsymbol{x}_0|\boldsymbol{x}_t)$通常是不够准确的，因此误差会持续累积。另外，$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)$在采样过程中会带有噪声，这个噪声可能会严重破坏刚刚预估出来的$\hat{\boldsymbol{x}}_0$信息，从而使得生成效果变差。

不过很幸运，大多数情况下，我们都可以基于$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)$这个简单的选择来衍生出一个新的结果。根据式$\eqref{eq:re-param}$，我们知道
\begin{equation}\begin{aligned}
\boldsymbol{x}_{t-1} \sim p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)\quad\Leftrightarrow&\,\quad\boldsymbol{x}_{t-1} = \boldsymbol{\mathcal{F}}_{t-1}(\boldsymbol{x}_0,\boldsymbol{\varepsilon}) \\
\boldsymbol{x}_t \sim p(\boldsymbol{x}_t|\boldsymbol{x}_0)\quad\Leftrightarrow&\,\quad\boldsymbol{x}_t = \boldsymbol{\mathcal{F}}_t(\boldsymbol{x}_0,\boldsymbol{\varepsilon})
\end{aligned}\end{equation}
假定$\boldsymbol{\mathcal{F}}_t(\boldsymbol{x}_0,\boldsymbol{\varepsilon})$关于$\boldsymbol{\varepsilon}$是可逆的，那么可以解出$\boldsymbol{\varepsilon} = \boldsymbol{\mathcal{F}}_t^{-1}(\boldsymbol{x}_0,\boldsymbol{x}_t)$，此时可以用解出来的这个$\boldsymbol{\varepsilon}$替换掉$\boldsymbol{\mathcal{F}}_{t-1}(\boldsymbol{x}_0,\boldsymbol{\varepsilon})$中的$\boldsymbol{\varepsilon}$，得到
\begin{equation}\boldsymbol{x}_{t-1} = \boldsymbol{\mathcal{F}}_{t-1}(\boldsymbol{x}_0,\boldsymbol{\mathcal{F}}_t^{-1}(\boldsymbol{x}_0,\boldsymbol{x}_t))\end{equation}
这就相当于
\begin{equation}p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \delta\big(\boldsymbol{x}_{t-1} - \boldsymbol{\mathcal{F}}_{t-1}(\boldsymbol{x}_0,\boldsymbol{\mathcal{F}}_t^{-1}(\boldsymbol{x}_0,\boldsymbol{x}_t))\big)\end{equation}
是一个同时依赖于$\boldsymbol{x}_t, \boldsymbol{x}_0$的$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$设计，$\boldsymbol{x}_t$分摊了$\boldsymbol{x}_{t-1}$对$\boldsymbol{x}_0$的部分依赖，并且消除了噪声，使得每一步生成的“进展”可以稳定地累积下来，因此用这个设计的反向过程往往有更好的效果。

此外，如果是$q(\boldsymbol{\varepsilon})$是标准正态分布，那么还可以得到更一般的结果，因为由正态分布的叠加性，我们可以得到
\begin{equation}\boldsymbol{x}_{t-1} = \boldsymbol{\mathcal{F}}_{t-1}(\boldsymbol{x}_0,\boldsymbol{\varepsilon})\quad\Leftrightarrow\quad\boldsymbol{x}_{t-1} = \boldsymbol{\mathcal{F}}_{t-1}(\boldsymbol{x}_0,\sqrt{1 - \tilde{\sigma}_t^2}\boldsymbol{\varepsilon}_1 + \tilde{\sigma}_t \boldsymbol{\varepsilon}_2)\end{equation}
这样一来，由$\boldsymbol{x}_0,\boldsymbol{x}_t$解出来的$\boldsymbol{\varepsilon}$可以只用来替换$\boldsymbol{\varepsilon}_1$或$\boldsymbol{\varepsilon}_2$中的一个，最终得到的$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$的采样过程就是
\begin{equation}\quad\boldsymbol{x}_{t-1} = \boldsymbol{\mathcal{F}}_{t-1}(\boldsymbol{x}_0,\sqrt{1 - \tilde{\sigma}_t^2}\boldsymbol{\mathcal{F}}_t^{-1}(\boldsymbol{x}_0,\boldsymbol{x}_t) + \tilde{\sigma}_t \boldsymbol{\varepsilon})\end{equation}

思考分析 #

至此，统一扩散模型UDM的理论框架已经构建完毕，下一篇文章我们会通过一些具体例子介绍如何从UDM框架推出已有的扩散模型结果，以及进一步得到一些新的结果，这一节我们来对全文的推理做一个思考分析。

看完全文，相信不少读者是比较懵的，因为本文的结果是建立在笔者前面对扩散模型的所有理解基础上总结出来的一个统一框架，总体的技术不算很难，但是逻辑上并不容易捋清楚。首先，本文的目标是“设计一个统一的扩散模型理论框架”，这个框架能够完成本文开头罗列出来的目标。“设计”的关键是把握住“自由”和“约束”，有一些部分是可以灵活选择的，有一些部分则是带有约束的，不能乱来的。

如果读者已经对现有生成扩散模型比较熟悉，想必就能领悟到扩散模型的本质思想就是“从破坏中学习建设”，因此“破坏”的方式理论上是可以随意选择的，“建设”则是需要学习的。当然，“破坏”的方式实际上也不是毫无约束，一般来说必须是“渐进式破坏”，这样我们才能学会“渐进式建设”。这样一来，我们就构建了式$\eqref{eq:re-param}$的破坏过程（前向过程），$t$用来描述破坏的进度，$\mathcal{F}$可以用来表示任意破坏方式，对原始数据$\boldsymbol{x}_0$也没有特别限制，至于$\boldsymbol{\varepsilon}$则用来描述破坏过程中可能存在的随机因素。这样，我们就建立了一个最一般的破坏过程。

至于建设，我们首先给出了分解式$\eqref{eq:p-factor}$，这是概率论本身给出的一个恒等式，我们可以将它理解为一个约束，也可以理解为是一个引导。怎么知道要往式$\eqref{eq:p-factor}$想呢？事后来看，前向过程是一个$\boldsymbol{x}_0\to \boldsymbol{x}_t$的过程，所以反向过程就应该尽量与$\boldsymbol{x}_t\to \boldsymbol{x}_0$联系起来，因此能联想到式$\eqref{eq:p-factor}$。

分解式$\eqref{eq:p-factor}$包含两个部分，其中$p(\boldsymbol{x}_0|\boldsymbol{x}_t)$已经很明确了，就是用$\boldsymbol{x}_t$来预测$\boldsymbol{x}_0$的概率，这个部分显然已经没有什么化简空间了，只能直接用模型来建模；另一部分$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$则是属于“自由设计”的范畴，它要求的话便于采样，其中的“约束”则是由一个恒等式$\eqref{eq:margin}$，这也是概率论本身给出的。至于后面的在这个约束之下去设计$p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0)$的过程，确实有些技巧性，这部分没有什么捷径，笔者也是结合已有的扩散模型工作思考了很久，才把这个过程捋清楚的。

总的来说，设计一个模型的时候，要时刻知道自己要什么（“自由”），这个想要的东西有什么限制（“约束”），在明确“自由”与“约束”的前提下，尽量借鉴已有的工作和所学的理论基础，不断往目标凑近。

文章小结 #

本文构建了一个新的扩散模型理论框架（Unified Diffusion Model，UDM），理论上它能够包含现有的生活扩散模型结果，并且允许更一般的扩散方式和数据类型。具体的例子我们下一篇文章再介绍。

转载到请包括本文地址：https://kexue.fm/archives/9262

更详细的转载事宜请参考：《科学空间FAQ》