简明条件随机场CRF介绍（附带纯Keras实现）

笔者去年曾写过博文《果壳中的条件随机场(CRF In A Nutshell)》，以一种比较粗糙的方式介绍了一下条件随机场（CRF）模型。然而那篇文章显然有很多不足的地方，比如介绍不够清晰，也不够完整，还没有实现，在这里我们重提这个模型，将相关内容补充完成。

本文是对CRF基本原理的一个简明的介绍。当然，“简明”是相对而言中，要想真的弄清楚CRF，免不了要提及一些公式，如果只关心调用的读者，可以直接移到文末。

图示 #

按照之前的思路，我们依旧来对比一下普通的逐帧softmax和CRF的异同。

逐帧softmax #

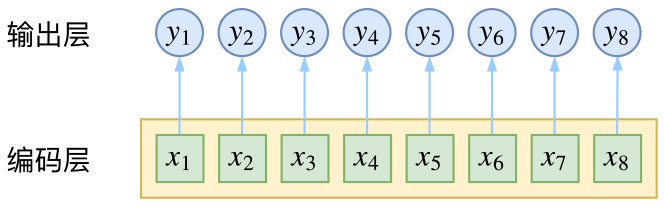
CRF主要用于序列标注问题，可以简单理解为是给序列中的每一帧都进行分类，既然是分类，很自然想到将这个序列用CNN或者RNN进行编码后，接一个全连接层用softmax激活，如下图所示

条件随机场 #

然而，当我们设计标签时，比如用s、b、m、e的4个标签来做字标注法的分词，目标输出序列本身会带有一些上下文关联，比如s后面就不能接m和e，等等。逐标签softmax并没有考虑这种输出层面的上下文关联，所以它意味着把这些关联放到了编码层面，希望模型能自己学到这些内容，但有时候会“强模型所难”。

而CRF则更直接一点，它将输出层面的关联分离了出来，这使得模型在学习上更为“从容”：

数学 #

当然，如果仅仅是引入输出的关联，还不仅仅是CRF的全部，CRF的真正精巧的地方，是它以路径为单位，考虑的是路径的概率。

模型概要 #

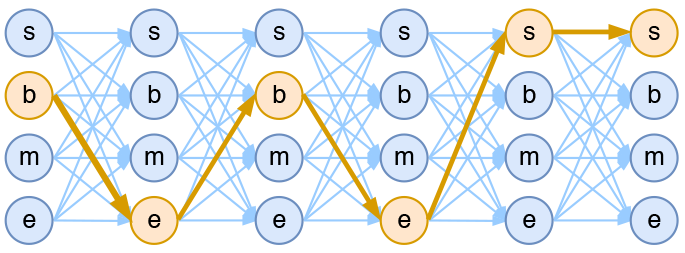
假如一个输入有$n$帧，每一帧的标签有$k$种可能性，那么理论上就有$k^n$种不同的输出。我们可以将它用如下的网络图进行简单的可视化。在下图中，每个点代表一个标签的可能性，点之间的连线表示标签之间的关联，而每一种标注结果，都对应着图上的一条完整的路径。

而在序列标注任务中，我们的正确答案是一般是唯一的。比如“今天天气不错”，如果对应的分词结果是“今天/天气/不/错”，那么目标输出序列就是bebess，除此之外别的路径都不符合要求。换言之，在序列标注任务中，我们的研究的基本单位应该是路径，我们要做的事情，是从$k^n$条路径选出正确的一条，那就意味着，如果将它视为一个分类问题，那么将是$k^n$类中选一类的分类问题！

这就是逐帧softmax和CRF的根本不同了：前者将序列标注看成是$n$个$k$分类问题，后者将序列标注看成是$1$个$k^n$分类问题。

具体来讲，在CRF的序列标注问题中，我们要计算的是条件概率
$$P(y_1,\dots,y_n|x_1,\dots,x_n)=P(y_1,\dots,y_n|\boldsymbol{x}),\quad \boldsymbol{x}=(x_1,\dots,x_n)\tag{1}$$
为了得到这个概率的估计，CRF做了两个假设：

假设一 该分布是指数族分布。

这个假设意味着存在函数$f(y_1,\dots,y_n;\boldsymbol{x})$，使得
$$P(y_1,\dots,y_n|\boldsymbol{x})=\frac{1}{Z(\boldsymbol{x})}\exp\Big(f(y_1,\dots,y_n;\boldsymbol{x})\Big)\tag{2}$$
其中$Z(\boldsymbol{x})$是归一化因子，因为这个是条件分布，所以归一化因子跟$\boldsymbol{x}$有关。这个$f$函数可以视为一个打分函数，打分函数取指数并归一化后就得到概率分布。

假设二 输出之间的关联仅发生在相邻位置，并且关联是指数加性的。

这个假设意味着$f(y_1,\dots,y_n;\boldsymbol{x})$可以更进一步简化为
$$\begin{aligned}f(y_1,\dots,y_n;\boldsymbol{x})=&h(y_1;\boldsymbol{x})+g(y_1,y_2;\boldsymbol{x})+h(y_2;\boldsymbol{x})+g(y_2,y_3;\boldsymbol{x})+h(y_3;\boldsymbol{x})\\
&+\dots+g(y_{n-1},y_n;\boldsymbol{x})+h(y_n;\boldsymbol{x})\end{aligned}\tag{3}$$
这也就是说，现在我们只需要对每一个标签和每一个相邻标签对分别打分，然后将所有打分结果求和得到总分。

线性链CRF #

尽管已经做了大量简化，但一般来说，$(3)$式所表示的概率模型还是过于复杂，难以求解。于是考虑到当前深度学习模型中，RNN或者层叠CNN等模型已经能够比较充分捕捉各个$y$与输入$\boldsymbol{x}$的联系，因此，我们不妨考虑函数$g$跟$\boldsymbol{x}$无关，那么
$$\begin{aligned}f(y_1,\dots,y_n;\boldsymbol{x})=h(y_1;\boldsymbol{x})+&g(y_1,y_2)+h(y_2;\boldsymbol{x})+\dots\\
+&g(y_{n-1},y_n)+h(y_n;\boldsymbol{x})\end{aligned}\tag{4}$$
这时候$g$实际上就是一个有限的、待训练的参数矩阵而已，而单标签的打分函数$h(y_i;\boldsymbol{x})$我们可以通过RNN或者CNN来建模。因此，该模型是可以建立的，其中概率分布变为
$$P(y_1,\dots,y_n|\boldsymbol{x})=\frac{1}{Z(\boldsymbol{x})}\exp\left(h(y_1;\boldsymbol{x})+\sum_{t=1}^{n-1}\Big[g(y_t,y_{t+1})+h(y_{t+1};\boldsymbol{x})\Big]\right)\tag{5}$$
这就是线性链CRF的概念。

归一化因子 #

为了训练CRF模型，我们用最大似然方法，也就是用
$$-\log P(y_1,\dots,y_n|\boldsymbol{x})\tag{6}$$
作为损失函数，可以算出它等于
$$-\left(h(y_1;\boldsymbol{x})+\sum_{t=1}^{n-1}\Big[g(y_t,y_{t+1})+h(y_{t+1};\boldsymbol{x})\Big]\right)+\log Z(\boldsymbol{x})\tag{7}$$
其中第一项是原来概率式的分子的对数，它目标的序列的打分，虽然它看上去挺迂回的，但是并不难计算。真正的难度在于分母的对数$\log Z(\boldsymbol{x})$这一项。

归一化因子，在物理上也叫配分函数，在这里它需要我们对所有可能的路径的打分进行指数求和，而我们前面已经说到，这样的路径数是指数量级的（$k^n$），因此直接来算几乎是不可能的。

事实上，归一化因子难算，几乎是所有概率图模型的公共难题。幸运的是，在CRF模型中，由于我们只考虑了临近标签的联系（马尔可夫假设），因此我们可以递归地算出归一化因子，这使得原来是指数级的计算量降低为线性级别。具体来说，我们将计算到时刻$t$的归一化因子记为$Z_t$，并将它分为$k$个部分
$$Z_t = Z^{(1)}_t + Z^{(2)}_t + \dots + Z^{(k)}_t\tag{8}$$
其中$Z^{(1)}_t,\dots,Z^{(k)}_t$分别是截止到当前时刻$t$中、以标签$1,\dots,k$为终点的所有路径的得分指数和。那么，我们可以递归地计算
$$\begin{aligned}Z^{(1)}_{t+1} = &\Big(Z^{(1)}_t G_{11} + Z^{(2)}_t G_{21} + \dots + Z^{(k)}_t G_{k1} \Big) H_{t+1}(1|\boldsymbol{x})\\
Z^{(2)}_{t+1} = &\Big(Z^{(1)}_t G_{12} + Z^{(2)}_t G_{22} + \dots + Z^{(k)}_t G_{k2} \Big) H_{t+1}(2|\boldsymbol{x})\\
&\qquad\qquad\vdots\\
Z^{(k)}_{t+1} =& \Big(Z^{(1)}_t G_{1k} + Z^{(2)}_t G_{2k} + \dots + Z^{(k)}_t G_{kk} \Big) H_{t+1}(k|\boldsymbol{x})
\end{aligned}\tag{9}$$
它可以简单写为矩阵形式
$$\boldsymbol{Z}_{t+1} = \boldsymbol{Z}_{t} \boldsymbol{G}\otimes H(y_{t+1}|\boldsymbol{x})\tag{10}$$
其中$\boldsymbol{Z}_{t}=\Big[Z^{(1)}_t,\dots,Z^{(k)}_t\Big]$；而$\boldsymbol{G}$是对矩阵$g$各个元素取指数后的矩阵（前面已经说过，最简单的情况下，$g$只是一个矩阵，代表某个标签到另一个标签的分数），即$\boldsymbol{G}_{ij}=e^{g_{ij}}$；而$H(y_{t+1}|\boldsymbol{x})$是编码模型$h(y_{t+1}|\boldsymbol{x})$（RNN、CNN等）对位置$t+1$的各个标签的打分的指数，即$H(y_{t+1}|\boldsymbol{x})=e^{h(y_{t+1}|\boldsymbol{x})}$，也是一个向量。式$(10)$中，$\boldsymbol{Z}_{t} \boldsymbol{G}$这一步是矩阵乘法，得到一个向量，而$\otimes$是两个向量的逐位对应相乘。

如果不熟悉的读者，可能一下子比较难接受$(10)$式。读者可以把$n=1,n=2,n=3$时的归一化因子写出来，试着找它们的递归关系，慢慢地就可以理解$(10)$式了。

动态规划 #

写出损失函数$-\log P(y_1,\dots,y_n|\boldsymbol{x})$后，就可以完成模型的训练了，因为目前的深度学习框架都已经带有自动求导的功能，只要我们能写出可导的loss，就可以帮我们完成优化过程了。

那么剩下的最后一步，就是模型训练完成后，如何根据输入找出最优路径来。跟前面一样，这也是一个从$k^n$条路径中选最优的问题，而同样地，因为马尔可夫假设的存在，它可以转化为一个动态规划问题，用viterbi算法解决，计算量正比于$n$。

动态规划在本博客已经出现了多次了，它的递归思想就是：一条最优路径切成两段，那么每一段都是一条（局部）最优路径。在本博客右端的搜索框键入“动态规划”，就可以得到很多相关介绍了，所以不再重复了～

实现 #

经过调试，基于Keras框架下，笔者得到了一个线性链CRF的简明实现，这也许是最简短的CRF实现了。这里分享最终的实现并介绍实现要点。

实现要点 #

前面我们已经说明了，实现CRF的困难之处是$-\log P(y_1,\dots,y_n|\boldsymbol{x})$的计算，而本质困难是归一化因子部分$Z(\boldsymbol{x})$的计算，得益于马尔科夫假设，我们得到了递归的$(9)$式或$(10)$式，它们应该已经是一般情况下计算$Z(\boldsymbol{x})$的计算了。

那么怎么在深度学习框架中实现这种递归计算呢？要注意，从计算图的视角看，这是通过递归的方法定义一个图，而且这个图的长度还不固定。这对于pytorch这样的动态图框架应该是不为难的，但是对于tensorflow或者基于tensorflow的Keras就很难操作了（它们是静态图框架）。

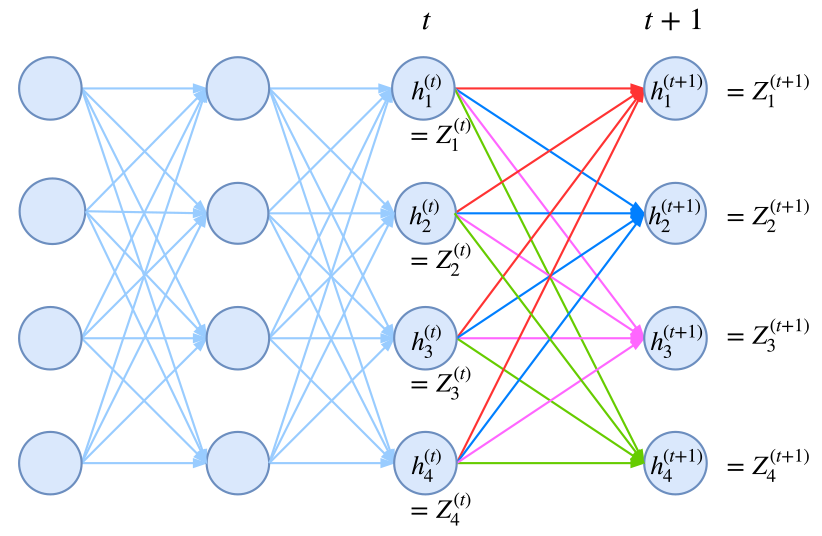
不过，并非没有可能，我们可以用封装好的rnn函数来计算！我们知道，rnn本质上就是在递归计算
$$\boldsymbol{h}_{t+1} = f(\boldsymbol{x}_{t+1}, \boldsymbol{h}_{t})\tag{11}$$
新版本的tensorflow和Keras都已经允许我们自定义rnn细胞，这就意味着函数$f$可以自行定义，而后端自动帮我们完成递归计算。于是我们只需要设计一个rnn，使得我们要计算的$\boldsymbol{Z}$对应于rnn的隐藏向量！

这就是CRF实现中最精致的部分了。

至于剩下的，是一些细节性的，包括：

1、为了防止溢出，我们通常要取对数，但由于归一化因子是指数求和，所以实际上是$\log\left(\sum_{i=1}^k e^{a_i}\right)$这样的格式，它的计算技巧是：
$$\log\left(\sum_{i=1}^k e^{a_i}\right)=A + \log\left(\sum_{i=1}^k e^{a_i-A}\right),\quad A = \max \{a_1,\dots,a_k\}$$
tensorflow和Keras中都已经封装好了对应的logsumexp函数了，直接调用即可；

2、对于分子（也就是目标序列的得分）的计算技巧，在代码中已经做了注释，主要是通过用“目标序列”点乘“预测序列”来实现取出目标得分；

3、关于变长输入的padding部分如何进行mask？我觉得在这方面Keras做得并不是很好。为了简单实现这种mask，我的做法是引入多一个标签，比如原来是s、b、m、e四个标签做分词，然后引入第五个标签，比如x，将padding部分的标签都设为x，然后可以直接在CRF损失计算时忽略第五个标签的存在，具体实现请看代码。

代码速览 #

纯Keras实现的CRF层，欢迎使用～

# -*- coding:utf-8 -*-

from keras.layers import Layer
import keras.backend as K


class CRF(Layer):
    """纯Keras实现CRF层
    CRF层本质上是一个带训练参数的loss计算层，因此CRF层只用来训练模型，
    而预测则需要另外建立模型。
    """
    def __init__(self, ignore_last_label=False, **kwargs):
        """ignore_last_label：定义要不要忽略最后一个标签，起到mask的效果
        """
        self.ignore_last_label = 1 if ignore_last_label else 0
        super(CRF, self).__init__(**kwargs)

    def build(self, input_shape):
        self.num_labels = input_shape[-1] - self.ignore_last_label
        self.trans = self.add_weight(name='crf_trans',
                                     shape=(self.num_labels, self.num_labels),
                                     initializer='glorot_uniform',
                                     trainable=True)

    def log_norm_step(self, inputs, states):
        """递归计算归一化因子
        要点：1、递归计算；2、用logsumexp避免溢出。
        技巧：通过expand_dims来对齐张量。
        """
        inputs, mask = inputs[:, :-1], inputs[:, -1:]
        states = K.expand_dims(states[0], 2)  # (batch_size, output_dim, 1)
        trans = K.expand_dims(self.trans, 0)  # (1, output_dim, output_dim)
        outputs = K.logsumexp(states + trans, 1)  # (batch_size, output_dim)
        outputs = outputs + inputs
        outputs = mask * outputs + (1 - mask) * states[:, :, 0]
        return outputs, [outputs]

    def path_score(self, inputs, labels):
        """计算目标路径的相对概率（还没有归一化）
        要点：逐标签得分，加上转移概率得分。
        技巧：用“预测”点乘“目标”的方法抽取出目标路径的得分。
        """
        point_score = K.sum(K.sum(inputs * labels, 2), 1, keepdims=True)  # 逐标签得分
        labels1 = K.expand_dims(labels[:, :-1], 3)
        labels2 = K.expand_dims(labels[:, 1:], 2)
        labels = labels1 * labels2  # 两个错位labels，负责从转移矩阵中抽取目标转移得分
        trans = K.expand_dims(K.expand_dims(self.trans, 0), 0)
        trans_score = K.sum(K.sum(trans * labels, [2, 3]), 1, keepdims=True)
        return point_score + trans_score  # 两部分得分之和

    def call(self, inputs):  # CRF本身不改变输出，它只是一个loss
        return inputs

    def loss(self, y_true, y_pred):  # 目标y_pred需要是one hot形式
        if self.ignore_last_label:
            mask = 1 - y_true[:, :, -1:]
        else:
            mask = K.ones_like(y_pred[:, :, :1])
        y_true, y_pred = y_true[:, :, :self.num_labels], y_pred[:, :, :self.num_labels]
        path_score = self.path_score(y_pred, y_true)  # 计算分子（对数）
        init_states = [y_pred[:, 0]]  # 初始状态
        y_pred = K.concatenate([y_pred, mask])
        log_norm, _, _ = K.rnn(self.log_norm_step, y_pred[:, 1:], init_states)  # 计算Z向量（对数）
        log_norm = K.logsumexp(log_norm, 1, keepdims=True)  # 计算Z（对数）
        return log_norm - path_score  # 即log(分子/分母)

    def accuracy(self, y_true, y_pred):  # 训练过程中显示逐帧准确率的函数，排除了mask的影响
        mask = 1 - y_true[:, :, -1] if self.ignore_last_label else None
        y_true, y_pred = y_true[:, :, :self.num_labels], y_pred[:, :, :self.num_labels]
        isequal = K.equal(K.argmax(y_true, 2), K.argmax(y_pred, 2))
        isequal = K.cast(isequal, 'float32')
        if mask == None:
            return K.mean(isequal)
        else:
            return K.sum(isequal * mask) / K.sum(mask)

除去注释和accuracy的代码，真正的CRF的代码量也就30行左右，可以说跟哪个框架比较都称得上是简明的CRF实现了吧～

用纯Keras实现一些复杂的模型，是一件颇有意思的事情。目前仅在tensorflow后端测试通过，理论上兼容theano、cntk后端，但可能要自行微调。

使用案例 #

我的Github中还附带了一个使用CNN+CRF实现的中文分词的例子，用的是Bakeoff 2005语料，例子是一个完整的分词实现，包括viterbi算法、分词输出等。

Github地址：https://github.com/bojone/crf/

相关的内容还可以看我之前的文章：

1、【中文分词系列】 4. 基于双向LSTM的seq2seq字标注

2、【中文分词系列】 6. 基于全卷积网络的中文分词

结语 #

终于介绍完了，希望大家有所收获，也希望最后的实现能对大家有所帮助～

转载到请包括本文地址：https://kexue.fm/archives/5542

更详细的转载事宜请参考：《科学空间FAQ》