简明条件随机场CRF介绍(附带纯Keras实现)
By 苏剑林 | 2018-05-18 | 436336位读者 |笔者去年曾写过博文《果壳中的条件随机场(CRF In A Nutshell)》,以一种比较粗糙的方式介绍了一下条件随机场(CRF)模型。然而那篇文章显然有很多不足的地方,比如介绍不够清晰,也不够完整,还没有实现,在这里我们重提这个模型,将相关内容补充完成。
本文是对CRF基本原理的一个简明的介绍。当然,“简明”是相对而言中,要想真的弄清楚CRF,免不了要提及一些公式,如果只关心调用的读者,可以直接移到文末。
图示 #
按照之前的思路,我们依旧来对比一下普通的逐帧softmax和CRF的异同。
逐帧softmax #
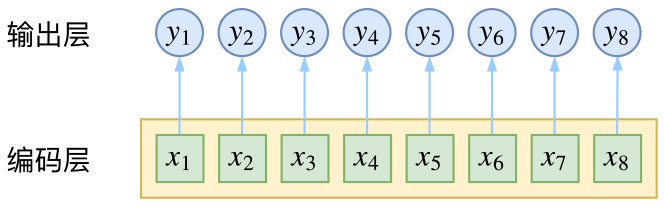
CRF主要用于序列标注问题,可以简单理解为是给序列中的每一帧都进行分类,既然是分类,很自然想到将这个序列用CNN或者RNN进行编码后,接一个全连接层用softmax激活,如下图所示
条件随机场 #
然而,当我们设计标签时,比如用s、b、m、e的4个标签来做字标注法的分词,目标输出序列本身会带有一些上下文关联,比如s后面就不能接m和e,等等。逐标签softmax并没有考虑这种输出层面的上下文关联,所以它意味着把这些关联放到了编码层面,希望模型能自己学到这些内容,但有时候会“强模型所难”。
而CRF则更直接一点,它将输出层面的关联分离了出来,这使得模型在学习上更为“从容”:
数学 #
当然,如果仅仅是引入输出的关联,还不仅仅是CRF的全部,CRF的真正精巧的地方,是它以路径为单位,考虑的是路径的概率。
模型概要 #
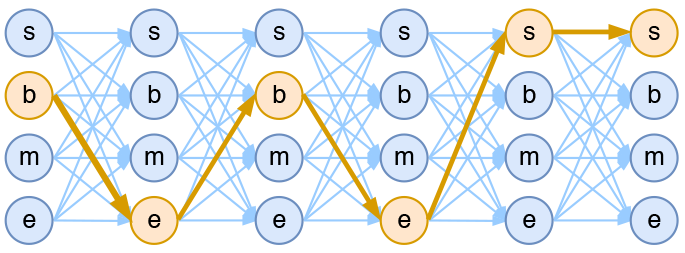
假如一个输入有$n$帧,每一帧的标签有$k$种可能性,那么理论上就有$k^n$种不同的输出。我们可以将它用如下的网络图进行简单的可视化。在下图中,每个点代表一个标签的可能性,点之间的连线表示标签之间的关联,而每一种标注结果,都对应着图上的一条完整的路径。
而在序列标注任务中,我们的正确答案是一般是唯一的。比如“今天天气不错”,如果对应的分词结果是“今天/天气/不/错”,那么目标输出序列就是bebess,除此之外别的路径都不符合要求。换言之,在序列标注任务中,我们的研究的基本单位应该是路径,我们要做的事情,是从$k^n$条路径选出正确的一条,那就意味着,如果将它视为一个分类问题,那么将是$k^n$类中选一类的分类问题!
这就是逐帧softmax和CRF的根本不同了:前者将序列标注看成是$n$个$k$分类问题,后者将序列标注看成是$1$个$k^n$分类问题。
具体来讲,在CRF的序列标注问题中,我们要计算的是条件概率
$$P(y_1,\dots,y_n|x_1,\dots,x_n)=P(y_1,\dots,y_n|\boldsymbol{x}),\quad \boldsymbol{x}=(x_1,\dots,x_n)\tag{1}$$
为了得到这个概率的估计,CRF做了两个假设:
假设一 该分布是指数族分布。
这个假设意味着存在函数$f(y_1,\dots,y_n;\boldsymbol{x})$,使得
$$P(y_1,\dots,y_n|\boldsymbol{x})=\frac{1}{Z(\boldsymbol{x})}\exp\Big(f(y_1,\dots,y_n;\boldsymbol{x})\Big)\tag{2}$$
其中$Z(\boldsymbol{x})$是归一化因子,因为这个是条件分布,所以归一化因子跟$\boldsymbol{x}$有关。这个$f$函数可以视为一个打分函数,打分函数取指数并归一化后就得到概率分布。
假设二 输出之间的关联仅发生在相邻位置,并且关联是指数加性的。
这个假设意味着$f(y_1,\dots,y_n;\boldsymbol{x})$可以更进一步简化为
$$\begin{aligned}f(y_1,\dots,y_n;\boldsymbol{x})=&h(y_1;\boldsymbol{x})+g(y_1,y_2;\boldsymbol{x})+h(y_2;\boldsymbol{x})+g(y_2,y_3;\boldsymbol{x})+h(y_3;\boldsymbol{x})\\
&+\dots+g(y_{n-1},y_n;\boldsymbol{x})+h(y_n;\boldsymbol{x})\end{aligned}\tag{3}$$
这也就是说,现在我们只需要对每一个标签和每一个相邻标签对分别打分,然后将所有打分结果求和得到总分。
线性链CRF #
尽管已经做了大量简化,但一般来说,$(3)$式所表示的概率模型还是过于复杂,难以求解。于是考虑到当前深度学习模型中,RNN或者层叠CNN等模型已经能够比较充分捕捉各个$y$与输入$\boldsymbol{x}$的联系,因此,我们不妨考虑函数$g$跟$\boldsymbol{x}$无关,那么
$$\begin{aligned}f(y_1,\dots,y_n;\boldsymbol{x})=h(y_1;\boldsymbol{x})+&g(y_1,y_2)+h(y_2;\boldsymbol{x})+\dots\\
+&g(y_{n-1},y_n)+h(y_n;\boldsymbol{x})\end{aligned}\tag{4}$$
这时候$g$实际上就是一个有限的、待训练的参数矩阵而已,而单标签的打分函数$h(y_i;\boldsymbol{x})$我们可以通过RNN或者CNN来建模。因此,该模型是可以建立的,其中概率分布变为
$$P(y_1,\dots,y_n|\boldsymbol{x})=\frac{1}{Z(\boldsymbol{x})}\exp\left(h(y_1;\boldsymbol{x})+\sum_{t=1}^{n-1}\Big[g(y_t,y_{t+1})+h(y_{t+1};\boldsymbol{x})\Big]\right)\tag{5}$$
这就是线性链CRF的概念。
归一化因子 #
为了训练CRF模型,我们用最大似然方法,也就是用
$$-\log P(y_1,\dots,y_n|\boldsymbol{x})\tag{6}$$
作为损失函数,可以算出它等于
$$-\left(h(y_1;\boldsymbol{x})+\sum_{t=1}^{n-1}\Big[g(y_t,y_{t+1})+h(y_{t+1};\boldsymbol{x})\Big]\right)+\log Z(\boldsymbol{x})\tag{7}$$
其中第一项是原来概率式的分子的对数,它目标的序列的打分,虽然它看上去挺迂回的,但是并不难计算。真正的难度在于分母的对数$\log Z(\boldsymbol{x})$这一项。
归一化因子,在物理上也叫配分函数,在这里它需要我们对所有可能的路径的打分进行指数求和,而我们前面已经说到,这样的路径数是指数量级的($k^n$),因此直接来算几乎是不可能的。
事实上,归一化因子难算,几乎是所有概率图模型的公共难题。幸运的是,在CRF模型中,由于我们只考虑了临近标签的联系(马尔可夫假设),因此我们可以递归地算出归一化因子,这使得原来是指数级的计算量降低为线性级别。具体来说,我们将计算到时刻$t$的归一化因子记为$Z_t$,并将它分为$k$个部分
$$Z_t = Z^{(1)}_t + Z^{(2)}_t + \dots + Z^{(k)}_t\tag{8}$$
其中$Z^{(1)}_t,\dots,Z^{(k)}_t$分别是截止到当前时刻$t$中、以标签$1,\dots,k$为终点的所有路径的得分指数和。那么,我们可以递归地计算
$$\begin{aligned}Z^{(1)}_{t+1} = &\Big(Z^{(1)}_t G_{11} + Z^{(2)}_t G_{21} + \dots + Z^{(k)}_t G_{k1} \Big) H_{t+1}(1|\boldsymbol{x})\\
Z^{(2)}_{t+1} = &\Big(Z^{(1)}_t G_{12} + Z^{(2)}_t G_{22} + \dots + Z^{(k)}_t G_{k2} \Big) H_{t+1}(2|\boldsymbol{x})\\
&\qquad\qquad\vdots\\
Z^{(k)}_{t+1} =& \Big(Z^{(1)}_t G_{1k} + Z^{(2)}_t G_{2k} + \dots + Z^{(k)}_t G_{kk} \Big) H_{t+1}(k|\boldsymbol{x})
\end{aligned}\tag{9}$$
它可以简单写为矩阵形式
$$\boldsymbol{Z}_{t+1} = \boldsymbol{Z}_{t} \boldsymbol{G}\otimes H(y_{t+1}|\boldsymbol{x})\tag{10}$$
其中$\boldsymbol{Z}_{t}=\Big[Z^{(1)}_t,\dots,Z^{(k)}_t\Big]$;而$\boldsymbol{G}$是对矩阵$g$各个元素取指数后的矩阵(前面已经说过,最简单的情况下,$g$只是一个矩阵,代表某个标签到另一个标签的分数),即$\boldsymbol{G}_{ij}=e^{g_{ij}}$;而$H(y_{t+1}|\boldsymbol{x})$是编码模型$h(y_{t+1}|\boldsymbol{x})$(RNN、CNN等)对位置$t+1$的各个标签的打分的指数,即$H(y_{t+1}|\boldsymbol{x})=e^{h(y_{t+1}|\boldsymbol{x})}$,也是一个向量。式$(10)$中,$\boldsymbol{Z}_{t} \boldsymbol{G}$这一步是矩阵乘法,得到一个向量,而$\otimes$是两个向量的逐位对应相乘。
如果不熟悉的读者,可能一下子比较难接受$(10)$式。读者可以把$n=1,n=2,n=3$时的归一化因子写出来,试着找它们的递归关系,慢慢地就可以理解$(10)$式了。
动态规划 #
写出损失函数$-\log P(y_1,\dots,y_n|\boldsymbol{x})$后,就可以完成模型的训练了,因为目前的深度学习框架都已经带有自动求导的功能,只要我们能写出可导的loss,就可以帮我们完成优化过程了。
那么剩下的最后一步,就是模型训练完成后,如何根据输入找出最优路径来。跟前面一样,这也是一个从$k^n$条路径中选最优的问题,而同样地,因为马尔可夫假设的存在,它可以转化为一个动态规划问题,用viterbi算法解决,计算量正比于$n$。
动态规划在本博客已经出现了多次了,它的递归思想就是:一条最优路径切成两段,那么每一段都是一条(局部)最优路径。在本博客右端的搜索框键入“动态规划”,就可以得到很多相关介绍了,所以不再重复了~
实现 #
经过调试,基于Keras框架下,笔者得到了一个线性链CRF的简明实现,这也许是最简短的CRF实现了。这里分享最终的实现并介绍实现要点。
实现要点 #
前面我们已经说明了,实现CRF的困难之处是$-\log P(y_1,\dots,y_n|\boldsymbol{x})$的计算,而本质困难是归一化因子部分$Z(\boldsymbol{x})$的计算,得益于马尔科夫假设,我们得到了递归的$(9)$式或$(10)$式,它们应该已经是一般情况下计算$Z(\boldsymbol{x})$的计算了。
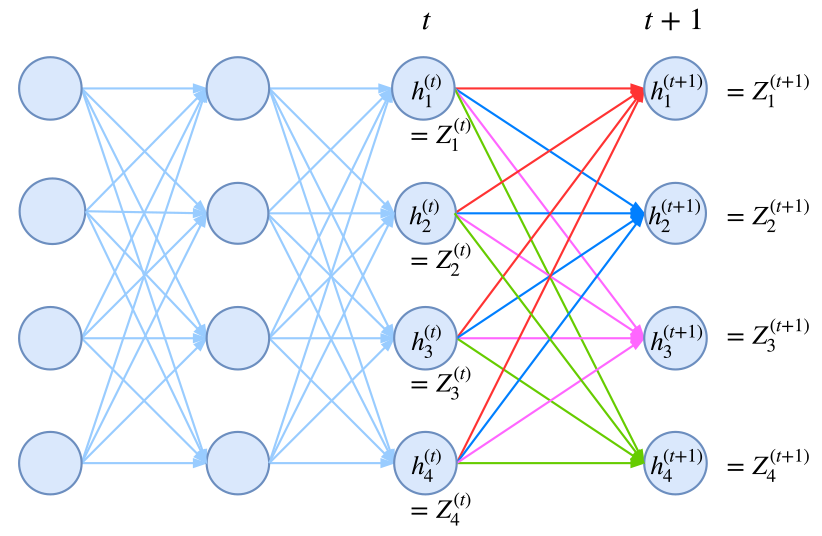
那么怎么在深度学习框架中实现这种递归计算呢?要注意,从计算图的视角看,这是通过递归的方法定义一个图,而且这个图的长度还不固定。这对于pytorch这样的动态图框架应该是不为难的,但是对于tensorflow或者基于tensorflow的Keras就很难操作了(它们是静态图框架)。
不过,并非没有可能,我们可以用封装好的rnn函数来计算!我们知道,rnn本质上就是在递归计算
$$\boldsymbol{h}_{t+1} = f(\boldsymbol{x}_{t+1}, \boldsymbol{h}_{t})\tag{11}$$
新版本的tensorflow和Keras都已经允许我们自定义rnn细胞,这就意味着函数$f$可以自行定义,而后端自动帮我们完成递归计算。于是我们只需要设计一个rnn,使得我们要计算的$\boldsymbol{Z}$对应于rnn的隐藏向量!
这就是CRF实现中最精致的部分了。
至于剩下的,是一些细节性的,包括:
1、为了防止溢出,我们通常要取对数,但由于归一化因子是指数求和,所以实际上是$\log\left(\sum_{i=1}^k e^{a_i}\right)$这样的格式,它的计算技巧是:
$$\log\left(\sum_{i=1}^k e^{a_i}\right)=A + \log\left(\sum_{i=1}^k e^{a_i-A}\right),\quad A = \max \{a_1,\dots,a_k\}$$
tensorflow和Keras中都已经封装好了对应的logsumexp函数了,直接调用即可;2、对于分子(也就是目标序列的得分)的计算技巧,在代码中已经做了注释,主要是通过用“目标序列”点乘“预测序列”来实现取出目标得分;
3、关于变长输入的padding部分如何进行mask?我觉得在这方面Keras做得并不是很好。为了简单实现这种mask,我的做法是引入多一个标签,比如原来是s、b、m、e四个标签做分词,然后引入第五个标签,比如x,将padding部分的标签都设为x,然后可以直接在CRF损失计算时忽略第五个标签的存在,具体实现请看代码。
代码速览 #
纯Keras实现的CRF层,欢迎使用~
# -*- coding:utf-8 -*-
from keras.layers import Layer
import keras.backend as K
class CRF(Layer):
"""纯Keras实现CRF层
CRF层本质上是一个带训练参数的loss计算层,因此CRF层只用来训练模型,
而预测则需要另外建立模型。
"""
def __init__(self, ignore_last_label=False, **kwargs):
"""ignore_last_label:定义要不要忽略最后一个标签,起到mask的效果
"""
self.ignore_last_label = 1 if ignore_last_label else 0
super(CRF, self).__init__(**kwargs)
def build(self, input_shape):
self.num_labels = input_shape[-1] - self.ignore_last_label
self.trans = self.add_weight(name='crf_trans',
shape=(self.num_labels, self.num_labels),
initializer='glorot_uniform',
trainable=True)
def log_norm_step(self, inputs, states):
"""递归计算归一化因子
要点:1、递归计算;2、用logsumexp避免溢出。
技巧:通过expand_dims来对齐张量。
"""
inputs, mask = inputs[:, :-1], inputs[:, -1:]
states = K.expand_dims(states[0], 2) # (batch_size, output_dim, 1)
trans = K.expand_dims(self.trans, 0) # (1, output_dim, output_dim)
outputs = K.logsumexp(states + trans, 1) # (batch_size, output_dim)
outputs = outputs + inputs
outputs = mask * outputs + (1 - mask) * states[:, :, 0]
return outputs, [outputs]
def path_score(self, inputs, labels):
"""计算目标路径的相对概率(还没有归一化)
要点:逐标签得分,加上转移概率得分。
技巧:用“预测”点乘“目标”的方法抽取出目标路径的得分。
"""
point_score = K.sum(K.sum(inputs * labels, 2), 1, keepdims=True) # 逐标签得分
labels1 = K.expand_dims(labels[:, :-1], 3)
labels2 = K.expand_dims(labels[:, 1:], 2)
labels = labels1 * labels2 # 两个错位labels,负责从转移矩阵中抽取目标转移得分
trans = K.expand_dims(K.expand_dims(self.trans, 0), 0)
trans_score = K.sum(K.sum(trans * labels, [2, 3]), 1, keepdims=True)
return point_score + trans_score # 两部分得分之和
def call(self, inputs): # CRF本身不改变输出,它只是一个loss
return inputs
def loss(self, y_true, y_pred): # 目标y_pred需要是one hot形式
if self.ignore_last_label:
mask = 1 - y_true[:, :, -1:]
else:
mask = K.ones_like(y_pred[:, :, :1])
y_true, y_pred = y_true[:, :, :self.num_labels], y_pred[:, :, :self.num_labels]
path_score = self.path_score(y_pred, y_true) # 计算分子(对数)
init_states = [y_pred[:, 0]] # 初始状态
y_pred = K.concatenate([y_pred, mask])
log_norm, _, _ = K.rnn(self.log_norm_step, y_pred[:, 1:], init_states) # 计算Z向量(对数)
log_norm = K.logsumexp(log_norm, 1, keepdims=True) # 计算Z(对数)
return log_norm - path_score # 即log(分子/分母)
def accuracy(self, y_true, y_pred): # 训练过程中显示逐帧准确率的函数,排除了mask的影响
mask = 1 - y_true[:, :, -1] if self.ignore_last_label else None
y_true, y_pred = y_true[:, :, :self.num_labels], y_pred[:, :, :self.num_labels]
isequal = K.equal(K.argmax(y_true, 2), K.argmax(y_pred, 2))
isequal = K.cast(isequal, 'float32')
if mask == None:
return K.mean(isequal)
else:
return K.sum(isequal * mask) / K.sum(mask)
除去注释和accuracy的代码,真正的CRF的代码量也就30行左右,可以说跟哪个框架比较都称得上是简明的CRF实现了吧~
用纯Keras实现一些复杂的模型,是一件颇有意思的事情。目前仅在tensorflow后端测试通过,理论上兼容theano、cntk后端,但可能要自行微调。
使用案例 #
我的Github中还附带了一个使用CNN+CRF实现的中文分词的例子,用的是Bakeoff 2005语料,例子是一个完整的分词实现,包括viterbi算法、分词输出等。
Github地址:https://github.com/bojone/crf/
相关的内容还可以看我之前的文章:
结语 #
终于介绍完了,希望大家有所收获,也希望最后的实现能对大家有所帮助~
转载到请包括本文地址:https://kexue.fm/archives/5542
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (May. 18, 2018). 《简明条件随机场CRF介绍(附带纯Keras实现) 》[Blog post]. Retrieved from https://kexue.fm/archives/5542
@online{kexuefm-5542,
title={简明条件随机场CRF介绍(附带纯Keras实现)},
author={苏剑林},
year={2018},
month={May},
url={\url{https://kexue.fm/archives/5542}},
}











October 24th, 2018
作者,你好。看了你的代码,似乎是在训练add_weight 的那个 self.trans ? 我最疑惑的地方就是这个trans 似乎只能代表一层转移矩阵啊, 但如果输入 今天/天气/不/错”,目标输出序列就是bebess,六个音节就有5层 K*K的转移矩阵。是我的理解有什么错误吗?
还有,不同层的转移矩阵trans肯定是不一样的,可是RNN最大的特点不是展开后,各个时间序列的 转移矩阵,也就是待训练的 W, 是一样的!!这怎么能用RNN来做了?
麻烦指教一下。。
大家都共用一个,这是线性链CRF的基本假设,在文章已经提到过了
好吧,感谢快速回复。另外,再请教一下,你定义的用来计算归一化因子的 log_norm_step (self, inputs, states) 方法, 对它进行调用是: K.rnn(self.log_norm_step, y_pred[:,1:], init_states, mask=mask)。
请问inputs, states这两个参数为什么可以不提供了?? 这是某种Keras的机制吗? 还有就是这个 rnn 的迭代次数如何确定啊!! 就是根据输入的序列长度吗?
求指教!!!
什么inputs, states不提供?不明白你说什么....
额,就是log_norm_step (self, inputs, states) 这个方法不是有3个参数吗, 然而K.rnn(self.log_norm_step, xx,xx,xx), 在这里用rnn 调用该方法,并没有传入这3个参数啊。。。
log_norm_step是递归执行的,根据inputs和init_states。
谢谢啊。最后问一下,这个RNN的递归次数是如何确定的了? 是输入语言序列的长度吗?
October 25th, 2018
@homehehe123|comment-10021
对的,根据inputs的长度,有多长就递归多少次
非常感谢!!
October 25th, 2018
楼主好,想请教两个问题:
1. 代码第31行是inputs+outputs我能理解,毕竟是取了log;可第30行是矩阵乘法,哪怕是取了log也不应该变成加吧?而且直接加的话维度也对不上;
2. 我不太熟悉NLP,所以想请教一下mask是用来干啥的呀……
就是变长输入的padding指的是什么呢…
1、30行的加法是对数加法,对应原来的两个数的乘法,留意states,trans的shape,states+trans事实上就是说“把矩阵任意两个数相乘,然后放在那里”(相当于张量的笛卡尔积);
2、30行的第二步是logsumexp,就是exp恢复原来的结果,然后sum求和(矩阵乘法就是笛卡尔积,然后求和),然后再取回对数;
3、mask就是用来处理变长的情况,NLP中句子的长度不是固定的,但是神经网络需要固定长度的输入,所以需要mask来告诉模型每一个句子的实际长度。
哦哦明白了!我才意识到张量加法可以broadcast,然后就说得通了:正好任意两个数相乘也是trans之后的"概率"的一部分~
多谢!
December 31st, 2018
您好,首先感谢您的分析。
有个地方没有很明白:10式下面有一句说“G是对g(yi,yj)各个元素取指数后的矩阵”,然后G就有各个分量G1,1,G2,1,...Gk,1。这里感觉表示符号有点乱。像5式中,只有g(y_k, y_{k+1}),而没有g(1,k)这样的。我的理解是,5式中g(y_i, y_{i+1})是一个k*k的矩阵,然后第a行第b列的元素表示:第i帧的标签为a而第j帧的标签为b的得分。
所以,如果10式的G只是把“g(yi,yj)各个元素取指数”,那么j应该还是只能等于i+1的吧?那么此时,G1,1,G2,1这些又代表什么呢?
你指出得没错,确实不应该这样表示,我修改了一下,请你指教。
January 4th, 2019
不好意思,还是没闹明白“G是对矩阵g_{ij}各个元素取指数后的矩阵”这句话,g_{ij}到底是一个矩阵还是多个矩阵?看前面朋友的回复,似乎在不同时刻,是共用一个g矩阵的,那这样的话,就应该没有g_{ij}而只有g了,g(y_{i}, y_{i+1})就是“第i张图的标签为y_i而第i+1张图的标签为y_i+1的得分”,所以的话,应该是G=e^{g}吧,也就是说G和g是大小相同的,只不过G是把g的所有元素给取了指数。
另外还有个技术层面的问题,我应该怎么观察loss函数里的变量呢?如果是一般的TensorFlow的程序,我可以把loss函数里的变量返回到主函数里,然后用sess.run把占位符填充上,就可以观察这个变量了,但是keras里似乎封装得太好了,以至于我没法观察。例如,第二十三行,log_norm_step函数里的states、trans、output这三个变量,我该怎么观察他们的实体值(而不仅仅是那个shape)?
$g$是矩阵,$g_{ij}$是矩阵的元素,也可以表示矩阵本身,这都是常见的用法。就算不知道,为什么要死抠字眼呢?(算了,我再改改描述好了)
另外,trans可以直接通过K.eval(crf. trans)来看,至于log_norm_step里边的states、outputs,我不认为你有能力在tf中观察它们的值(不要跟我说理论上可以,你实践了再说,tf中也有crf的实现,也是用rnn来实现的,观察rnn的中间值,其实并不容易......)。
g的事儿向你道个歉。主要是:1、CRF网上太多博客,哪一个都不一样,我是初学者,以前没有学过相关的内容,就有点搞晕了;2、一般都是单个黑体字母表示矩阵,而带下标或者括号的是表示矩阵里的某个元素,我就给误解了,也是怪我手比较生(估计熟悉的人很快能看懂)。
观察变量的问题,我现在还没到观察rnn中间值那么高端的地步,就是最基础的观察loss函数里的变量。我试着把K.eval(crf. trans)这句加到word_seg.py的model.compile那句的后面,但是发现并没有输出crf. trans的值。
然后我看到github上的回答,“标量函数可以直接作为metrics添加到输出显示中”,这个我倒是实现了,就是在crf_keras.py里再定义一个函数,让他返回self.trans:
$\quad$$\quad$def check_trans(self, y_true, y_pred):
$\quad$$\quad$$\quad$return self.trans
然后在主函数word_seg.py里的model.compile里修改:
model.compile(loss=crf.loss, # 用crf自带的loss
$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$optimizer='adam',
$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$metrics=[crf.accuracy, crf.check_trans] # 把crf里的trans也输出出来看一下。
$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$)
这个确实是可以输出的,大概会是这个样子:
1/200 [..............................] - ETA: 6:31 - loss: 2.6031 - accuracy: 0.0718 - check_trans: 0.1304
6/200 [..............................] - ETA: 1:05 - loss: 2.5980 - accuracy: 0.8453 - check_trans: 0.1285
11/200 [>.............................] - ETA: 35s - loss: 2.1312 - accuracy: 0.9156 - check_trans: 0.1264
16/200 [=>............................] - ETA: 24s - loss: 1.5326 - accuracy: 0.9420 - check_trans: 0.1244
21/200 [==>...........................] - ETA: 18s - loss: 1.1696 - accuracy: 0.9558 - check_trans: 0.1227
26/200 [==>...........................] - ETA: 15s - loss: 0.9447 - accuracy: 0.9643 - check_trans: 0.1213
但这样也有个问题,就是他是把self.trans当成标量输出了,但是实际上他应该是一个shape=(4,4)的矩阵啊,输出的似乎是有问题的。。
所以还请具体指教一下,谢谢~
道歉倒不至于,因为也没有亏欠什么~~我就是吐槽一下,别见怪。
模型训练完之后,直接K.eval(self.trans)就可以看到整个trans矩阵的值了。
难道你是想观察训练过程中trans的变化情况?如果这样的话,自定义一个callback类,定义里边的on_batch_end函数,把K.eval(self.trans)放到里边(把trans的值输出到文件中)。
January 6th, 2019
self.trans的问题,现在可以了,应该是把K.eval(self.trans)放在model.fit_generator的后面。我原来是放在compile后面就不行。
log_norm_step里边的states、outputs的问题,我的目的是把程序实现和公式对应起来。我想了个办法,从generator里弄出来一个批次的数据,然后送到tf里去执行一步,就是下面的程序:
$\quad$gen = train_generator()
$\quad$one_batch = gen.__next__()
$\quad$X_check = one_batch[0] # (batch_size, 4),数据的实体值
$\quad$Y_check_true = one_batch[1] # (batch_size, 4, 5),(1热)标签的实体值
$\quad$Y_check_pred = model.predict(X_check) # (batch_size, 4, 5),上面网络输出的结果,就是那个tag_score_crf。
$\quad$check_tag_score_crf = model.predict(X_check) # (128, 4, 128)
$\quad$import tensorflow as tf
$\quad$Y_check_true_pl = tf.placeholder(tf.float32, [batch_size, 4, 5]) # 金标准的占位符
$\quad$Y_check_pred_pl = tf.placeholder(tf.float32, [batch_size, 4, 5]) # 预测值的占位符
$\quad$loss, y_true, y_pred, init_states, rnn_results, log_norm, path_score, new_states_of_step1 = \
$\quad$$\quad$crf.loss_check(Y_check_true_pl, Y_check_pred_pl)
$\quad$feed_dict = {Y_check_true_pl: Y_check_true, Y_check_pred_pl: Y_check_pred}
$\quad$sess = tf.Session()
$\quad$init = tf.initialize_all_variables()
$\quad$sess.run(init)
$\quad$_loss, _y_true, _y_pred, _init_states, _rnn_results, _log_norm, _path_score, _new_states_of_step1 = \
$\quad$$\quad$sess.run([loss, y_true, y_pred, init_states, rnn_results, log_norm, path_score, new_states_of_step1], feed_dict=feed_dict) # 都是loss_check函数里的变量
这个方法可以把loss函数里的所有变量都给弄出来实体值,然后我把原来的loss函数复制一个,命名为loss_check,然后加了一句:
$\quad$new_states_of_step1, _ = self.log_norm_step(y_pred[:,1,:], init_states)
并把这个new_states_of_step1返回,就可以观察到一个时间步长里的inputs+outputs,同样可以返回观察states等变量。我的理解,在这一步中,那个inputs应该就是10式中的$h(y_{2}; \textbf{x})$(取指数后就是$H(y_{2}; \textbf{x})$);states应该是$z_{1}$(取指数后就是$Z_{1}$);outputs就是实现$Z_{1}G$并且还原回log域,然后和inputs相加就对应正常域中的矩阵逐元素相乘。所以,K.rnn里迭代调用这个self.log_norm_step,就可以输出$Z_{1}$,$Z_{2}$,...$Z_{4}$。
感觉上面的理解似乎能说通,但是,我发现new_states_of_step1的值是0~120之间的数(第一列的数比较大,100左右,后面的列都比较小。20~40左右),事实上我发现init_states里的数都是-10~50之间的(也是第一列比较大)。这些都应该是对应取指数之前的数,我不太清楚这个是否正常,是我实现错了,还是在“log域”的数真的会有这么大?
我感觉是这样做是不对的。
您觉得问题出在哪里?是Y_check_pred预测值不能代表crf.loss函数的输入(但我感觉这儿应该是可以的,因为Y_check_pred、Y_check_true和X_check应该对应的是同一个),还是不能单独把那个self.log_norm_step函数拿出来,用一个时间补偿单步调试执行呢(这个我自己确实也不太确定,我写程序的时候就想着,把输入的前2个时间步长,当成是只有2个时间步长的输入了)?
你自己插入session让我觉得有问题
January 13th, 2019
楼主好,想请教一下,path_score函数里提到的技巧是,用“预测”点乘“目标”的方法抽取出目标路径的得分,这个怎么理解呢?我的理解是,点乘后的结果就是单词中所有汉字取某个标签的概率,然后用这些概率去计算得分、训练self.trans转移矩阵。这个理解是否get到你程序里的point了?
然后还有个,测试的时候,如果没有“目标”,该怎么办呢?我看到程序是直接用训练好的CNN模型预测每个汉字的标签,然后抽取出来trans矩阵,把标签和trans矩阵都放到viterbi算法里预测最终标签。但,直觉上感觉,训练的时候,用金标准标签抽取了正确的路径训练那个self.trans矩阵,但是测试的时候,是把所有的路径都用那个self.trans预测的。也就是说,训练和测试时候的预测过程是不一样的吗?
1、参考这个https://kexue.fm/archives/4122
2、训练和测试过程肯定不一样....在概率图模型中,训练叫做“学习”,测试叫做“推断”,两个都是难题。
看了链接,链接是用1热标签编码汉字,然后用查表操作代替矩阵乘法获得最终的logits。但我还是不明白,那个logits和这里的路径分数有什么关系呢?
第二个问题我自己再看看。
假设a=2,b=[1, 2, 3, 4],我要取出b的第a个元素,但是我无法b[a]这样操作,但是我有办法将a转换为c=[0, 0, 1, 0],然后sum(c * b)=3,成功提取出来了。
其实你应该把步骤换过来,读代码的时候,应该要这样子:
1、这一行是做什么的?
2、我来写会怎么写?
3、作者是怎么写的?
而不是一下子就到了第三步。当你真的去思考了“我来写会怎么写”之后,你就会明白其中的困难所在,你就会明白我这样写的无奈之处。
谢谢,现在明白了。我前几天明白提取元素的操作,但是没明白为什么要提取。然后我是在想我最早的第2个问题的时候想明白的。
因为这儿训练和测试是很不一样的。训练的时候有金标准,所以只需要用金标准提取路径就可以计算出来7式,所以要在path_score中用金标准标签和预测标签(或者转移矩阵self.trans)相乘,这样就把预测错的路径得分都删掉了,然后把对的得分相加,就得到7式中第一项负号里的部分。
然后,测试的时候,因为没有金标准了,只能用训练好的转移矩阵求出来每一种路径的得分,然后选择路径得分最大的,作为最终预测的结果
祝贺~你的理解已经完全正确了。
嗯嗯,谢谢你的博客~~
January 29th, 2019
这是我看过写CRF最清晰的文章了,多谢!
February 28th, 2019
线性链CRF 那一段划线处,应该是"y与输入x之间的关系",原文是"输出x";
感谢细致阅读,已经修正。
March 9th, 2019
谢谢你的分享,这对我很有帮助!!!