行星的逆行,顺行和留(计算公式)

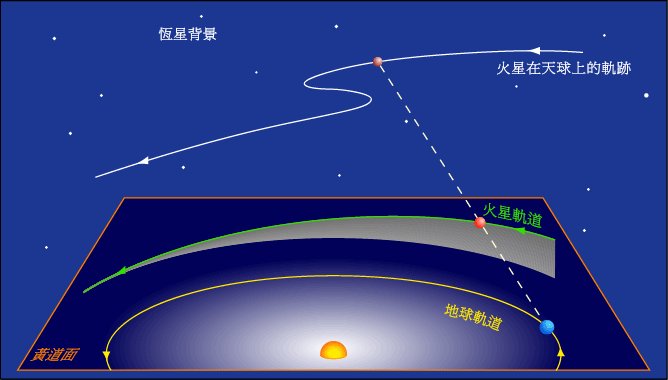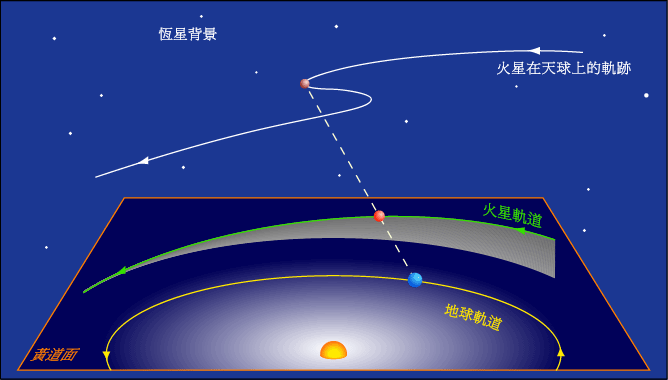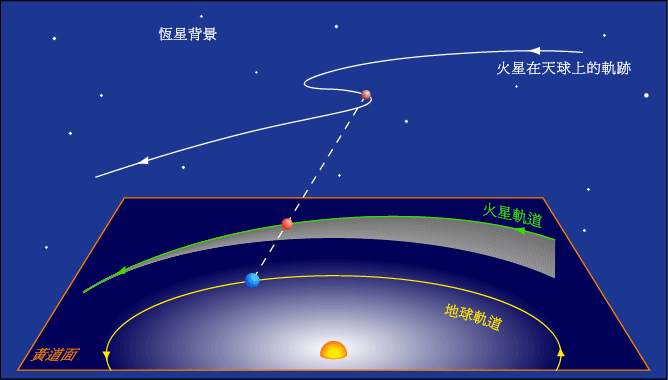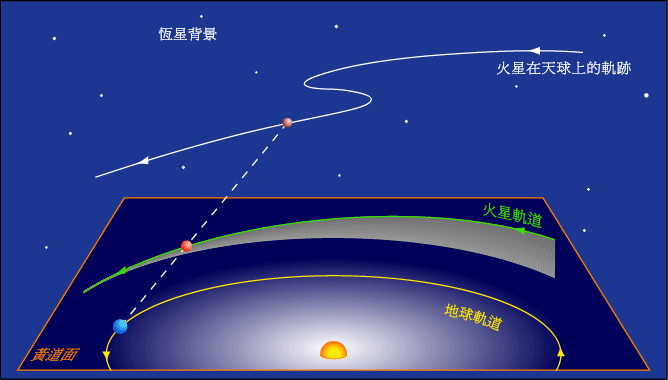
由于地球自西向东自转和公转，所以地球上所看到的绝大多数星体都是东升西落的，所以我们把星体在天空中自东向西的运动称为“顺行”，自西向东被称为“逆行”。由于地球和行星的共同运动，地外外行星在“冲”的前后一段时间内会出现“逆行”的现象（地内行星则相反）。而逆行与顺行之间的那一天（应该说那一时刻），就被称为“留”。也就是说，行星“留”过后，行星在天空中的运动方向由顺行变为逆行，或者由逆行变为顺行。

下面是引用维基百科关于行星的顺逆行现象的说明：

从地球上观察，行星在天空中运行的路径会周期性的改变运动的方向。虽然所有的恒星和行星，在回应地球自转的基础下，看起来每夜都是由东向西运行的，但是在外侧的行星都常都会相对于恒星缓缓的由西向东移动。这种运动是行星的正常运动，因此被认为是顺行。但是，因为地球的轨道周期短于外侧行星的轨道周期，因此会周期性的超越外侧的行星，就像一辆速度较快的车在多条车道的高速公路上一样。当发生这种情况时，原本向东运行的行星会先停下，然后后退像栋运行，然后当地球在轨道上超越行星之后，看起来又恢复正常由西向东的运动。内侧的水星和金星也会在相同的机制下呈现逆行的运动，然而它们的退行周期也和太阳的会合周期结合在一起。解释视退行运动的机制是和外行星一样的，小行星和古柏带天体（包括冥王星）都有展现出视退行运动。

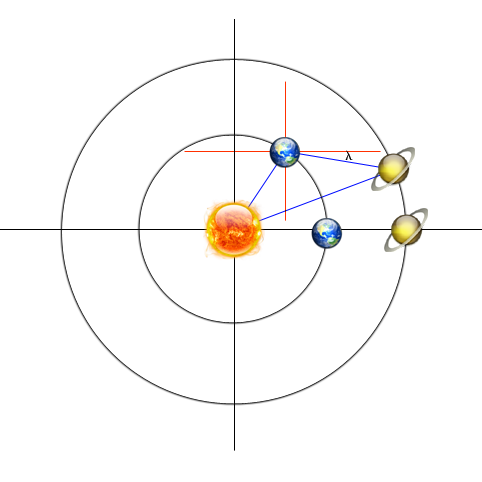
那么，行星每一次逆行要多久的时间呢？我们不妨来考虑一个最简单的模型：行星在同一轨道平面内做圆周运动。选择行星冲日的时间为原点，那么我们可以列出以地球为参照物的行星运动方程：
$$\begin{aligned}y=R_2 \sin(\omega_2 t)-R_1 \sin(\omega_1 t) \\ x=R_2 \cos(\omega_2 t)-R_1 \cos(\omega_1 t)\end{aligned}$$

$R,\omega=\frac{2\pi}{T}$分别是轨道半径和角速度（1是地球，2是地外行星）。很显然，行星的顺行和逆行取决于$\dot{\lambda}=\frac{d\lambda}{dt}$的正负（正顺逆负），“留”就是$\dot{\lambda}$等于0的情况。在以地球为原点的坐标系中：
$$\tan\lambda=\frac{R_2 \sin(\omega_2 t)-R_1 \sin(\omega_1 t)}{R_2 \cos(\omega_2 t)-R_1 \cos(\omega_1 t)}$$

对两边求导数
$$\begin{aligned}\frac{\dot{\lambda}}{cos^2 \lambda}=\Bigg\{\Big[R_2 \omega_2 cos(\omega_2 t)-R_1 \omega_1 cos(\omega_1 t)\Big]\Big[R_2 cos(\omega_2 t)-R_1 cos(\omega_1 t)\Big]\\
+\Big[R_2 \omega_2 \sin(\omega_2 t)-R_1 \omega_1 \sin(\omega_1 t)\Big]\Big[R_2 \sin(\omega_2 t)-R_1 \sin(\omega_1 t)\Big]\Bigg\}\\
\div \Bigg[R_2 \cos(\omega_2 t)-R_1 \cos(\omega_1 t)\Bigg]^2\end{aligned}$$

令分子为0，则有
$$\omega_1 R_1^2+\omega_2 R_2^2-(\omega_1+\omega_2)R_1 R_2 \cos(\omega_1 t-\omega_2 t)=0$$

于是行星逆行的时间
$$t_0=\frac{\arccos\left(\frac{\omega_1 R_1^2+\omega_2 R_2^2}{(\omega_1+\omega_2)R_1 R_2}\right)}{\omega_1-\omega_2}$$

这仅仅计算了“冲”之后的逆行时间，在冲之前，应该有一段相反而相等的过程，所以，行星逆行的时间为：
$$t=\frac{2\arccos\left(\frac{\omega_1 R_1^2+\omega_2 R_2^2}{(\omega_1+\omega_2)R_1 R_2}\right)}{\omega_1-\omega_2}$$

对于地内行星，虽然它们在下合的时候运行的速度比地球快，但是在地球上看，它们的运动方向仍然是是“顺时针”的，所以也就意味着此时是逆行。完全也可以用上述公式！

转载到请包括本文地址：https://kexue.fm/archives/608

更详细的转载事宜请参考：《科学空间FAQ》