VQ的又一技巧：给编码表加一个线性变换

在《VQ的旋转技巧：梯度直通估计的一般推广》中，我们介绍了VQ（Vector Quantization）的Rotation Trick，它的思想是通过推广VQ的STE（Straight-Through Estimator）来为VQ设计更好的梯度，从而缓解VQ的编码表坍缩、编码表利用率低等问题。

无独有偶，昨天发布在arXiv上的论文《Addressing Representation Collapse in Vector Quantized Models with One Linear Layer》提出了改善VQ的另一个技巧：给编码表加一个线性变换。这个技巧单纯改变了编码表的参数化方式，不改变VQ背后的理论框架，但实测效果非常优异，称得上是简单有效的经典案例。

基础 #

由于在《VQ-VAE的简明介绍：量子化自编码器》、《简单得令人尴尬的FSQ：“四舍五入”超越了VQ-VAE》等文章中我们已经多次介绍了VQ和VQ-VAE了，所以这里不再娓娓道来，直接给出普通AE和VQ-VAE的数学形式：
\begin{align}
\text{AE:}&\qquad z = encoder(x),\quad \hat{x}=decoder(z),\quad \mathcal{L}=\Vert x - \hat{x}\Vert^2 \\[12pt]
\text{VQ-VAE:}&\qquad\left\{\begin{aligned}
z =&\, encoder(x)\\[5pt]
z_q =&\, z + \text{sg}[q - z],\quad q = \mathop{\text{argmin}}_{e\in\{e_1,e_2,\cdots,e_K\}} \Vert z - e\Vert\\
\hat{x} =&\, decoder(z_q)\\[5pt]
\mathcal{L} =&\, \Vert x - \hat{x}\Vert^2 + \beta\Vert q - \text{sg}[z]\Vert^2 + \gamma\Vert z - \text{sg}[q]\Vert^2
\end{aligned}\right.\label{eq:vqvae}
\end{align}

再次强调老生常谈的一点：VQ-VAE不是VAE，它只是一个加上了VQ的AE，没有VAE的生成能力。而VQ则是将任意向量映射为编码表中与它最邻近的向量的操作，这个操作本身具有不可导的特性，所以通过STE来为encoder设计了梯度，并且新增了$\beta,\gamma$这两项损失，来为编码表提供梯度，同时也起到规整encoder表征的作用。

改动 #

论文将自己所提方法称为SimVQ，但没有解释Sim是什么含义，笔者猜测Sim是Simple的缩写，因为SimVQ的改动确实太Simple了：
\begin{equation}
\text{SimVQ-VAE:}\qquad\left\{\begin{aligned}
z =&\, encoder(x)\\[5pt]
z_q =&\, z + \text{sg}[q\color{red}{W} - z],\quad q = \mathop{\text{argmin}}_{e\in\{e_1,e_2,\cdots,e_K\}} \Vert z - e\color{red}{W}\Vert\\
\hat{x} =&\, decoder(z_q)\\[5pt]
\mathcal{L} =&\, \Vert x - \hat{x}\Vert^2 + \beta\Vert q\color{red}{W} - \text{sg}[z]\Vert^2 + \gamma\Vert z - \text{sg}[q\color{red}{W}]\Vert^2\end{aligned}\right.
\end{equation}
没错，就只是在编码表多乘了一个矩阵$W$，其他原封不动。

如果原本就是用式$\eqref{eq:vqvae}$训练VQ的，那么SimVQ可以直接简单上；如果原本是用EMA来更新编码表的（即$\beta=0$，然后用另外的滑动平均过程来更新编码表，这是VQ-VAE-2及后续一些模型的做法，在数学上等价于用SGD来优化编码表损失，而其他损失则可以用Adam等非SGD优化器），那么则需要取消这个操作，重新引入$\beta$项来端到端优化。

可能马上有读者质疑：这不就是将编码表的参数化从$E$改为$EW$吗？$EW$可以合并成一个矩阵，等价于一个新的$E$，按道理不改变模型的理论能力？是的，SimVQ对模型能力来说是不变的，但对SGD、Adam来说却是变的，它会改变优化器的学习过程，从而影响学习结果的好坏。

实验 #

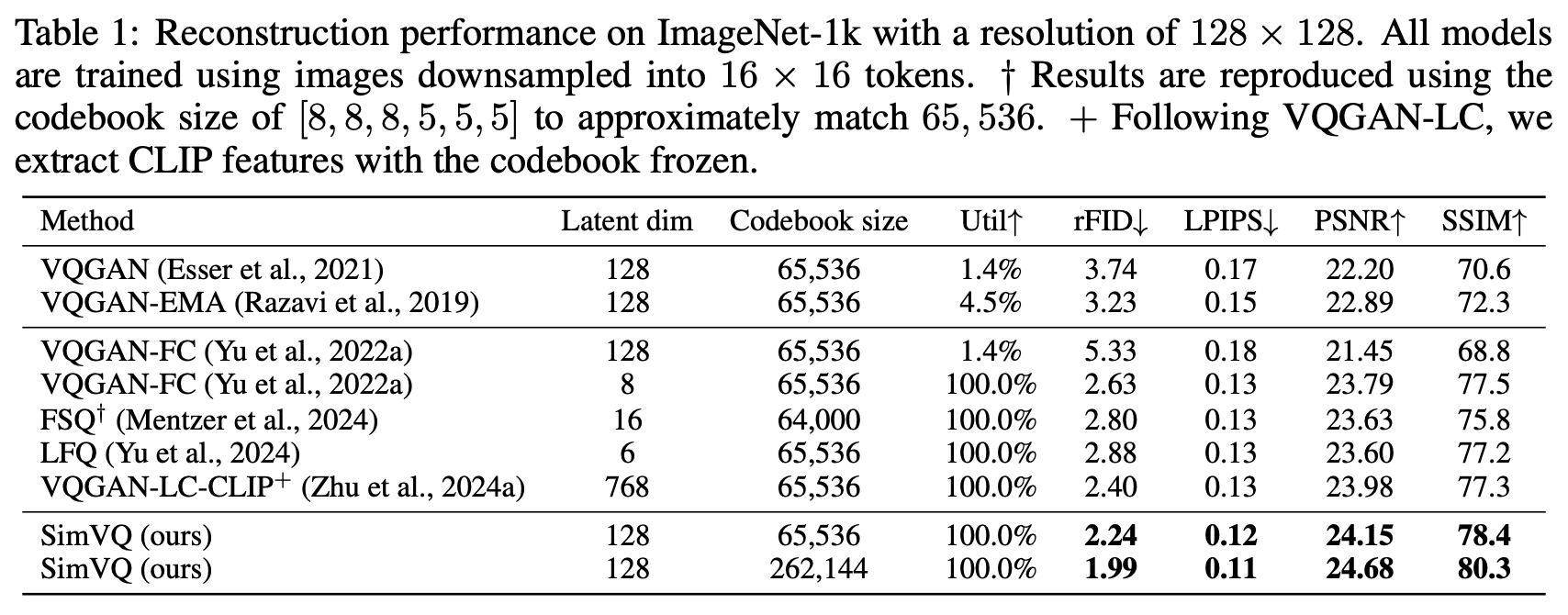
进一步思考和分析之前，我们先看看SimVQ的实验效果。SimVQ做了视觉和音频的实验，比较有代表性的是Table 1：

根据论文的描述，SimVQ的代码就是在第一行VQGAN的代码上改的，改动就只有往VQ层插入了个线性变换，然后提升就非常显著了，不仅在相同编码表大小下达到了最优的重构质量，还能通过增加编码表大小进一步提高重构质量，这足以体现SimVQ的魅力——简单且有效。

笔者也在自己之前写的VQ-VAE代码上做了尝试，实测显示这个线性变换的加入，明显加速了VQ-VAE的收敛速度，并且最终的重构损失也有所降低。笔者还实验了$W$取对角阵的变体，这时候就相当于每个编码向量都element-wise地与一个参数向量（全一初始化）相乘，结果显示这样的变体也能起到相近的效果，介乎VQ与SimVQ之间。

分析 #

直观来想，VQ对编码表的更新是比较“孤立”的，比如某个样本$z$被VQ为$q$，那么这个样本的梯度就只会影响$q$，不会影响编码表里的其他向量；但SimVQ不同，它不单会更新$q$，还会更新$W$，从几何意义上看，$W$就相当于编码表的基底，一旦更新$W$，那么整个编码表就会更新了。所以说，SimVQ使得整个编码表的“联动”更为密切，从而更有机会找到更优的解，而不是陷入“各自为政”的局部最优。

那为什么SimVQ能提高编码表的利用率呢？这个其实也不难理解。再次根据$W$是编码表基底的解释，如果编码表利用率过低，那么$W$就会出现“各向异性”，即基底偏向于那些被利用起来的编码，可是一旦基底发生这种变化，那么它的线性组合应该也是偏向于被利用起来的编码，从而利用率不会太低。说白了，可学习的基底会自动让自己的利用率变高，从而让整个编码表的利用率都提高起来。

我们也可以从数学公式角度来描述这个过程。假设优化器为SGD，那么VQ中编码$e_i$的更新为
\begin{equation}e_i^{(t+1)} = e_i^{(t)} - \eta\frac{\partial \mathcal{L}}{\partial e_i^{(t)}}\end{equation}
这样如果当前批次中$e_i$没有被选中，那么$\frac{\partial \mathcal{L}}{\partial e_i^{(t)}}$为零，当前编码表就不更新了。但如果$e_i$被参数化为$q_i W$，那么
\begin{equation}\begin{aligned}
q_i^{(t+1)} =&\, q_i^{(t)} - \eta\frac{\partial \mathcal{L}}{\partial q_i^{(t)}} = q_i^{(t)} - \eta \frac{\partial \mathcal{L}}{\partial e_i^{(t)}} W^{(t)}{}^{\top}\\
W^{(t+1)} =&\, W^{(t)} - \eta\frac{\partial \mathcal{L}}{\partial W^{(t)}} = W^{(t)} - \eta \sum_i q_i^{(t)}{}^{\top}\frac{\partial \mathcal{L}}{\partial e_i^{(t)}} \\
e_i^{(t+1)}=&\,q_i^{(t+1)}W^{(t+1)}\approx e_i^{(t)} - \eta\left(\frac{\partial \mathcal{L}}{\partial e_i^{(t)}} W^{(t)}{}^{\top}W^{(t)} + q_i^{(t)}\sum_i q_i^{(t)}{}^{\top}\frac{\partial \mathcal{L}}{\partial e_i^{(t)}}\right)
\end{aligned}\end{equation}
可以看到：

1、$W$是基于全体被选中的编码的梯度之和来更新的，所以它自然会更倾向于高利用率方向；

2、由于$q_i^{(t)}\sum_i q_i^{(t)}{}^{\top}\frac{\partial \mathcal{L}}{\partial e_i^{(t)}}$的存在，不管编码$i$有没有被选中，它的更新都几乎不会为零；

3、$q_i^{(t)}\sum_i q_i^{(t)}{}^{\top}\frac{\partial \mathcal{L}}{\partial e_i^{(t)}}$相当于是高利用率方向的投影，它使得每个编码都往高利用率方向走。

然而，物极必反，如果全体编码都使劲往高利用率方向走，那么反而可能会导致编码表坍缩（codebook collapse），因此SimVQ默认采用了一个很保守的策略：只更新$W$，所有的$q$在随机初始化后就不更新了，这样一来就几乎杜绝了编码表坍缩的可能性。好消息是，在适当的编码维度下，实验显示$q,W$都更新和只更新$W$的表现都差不多，所以读者可以按照自己的偏好选择具体的形式。

延伸 #

抛开VQ的背景，像SimVQ这种引入额外的参数但又在数学上等价，即不改变模型的理论拟合能力，只改变优化过程的动力学的做法，我们称为“过参数化（Overparameterization）”。

过参数化在神经网络中并不鲜见，比如现在模型的主流架构是Pre Norm即$x + f(\text{RMSNorm}(x))$，RMSNorm最后所乘的$\gamma$向量通常都是过参数化的，因为$f$的第一层通常就是线性变换，比如Attention是线性变换投影到Q、K、V，FFN是线性变换来升维，等等，这些模型在推理阶段$\gamma$向量完全可以合并到$f$的线性变换中，但鲜有看到在训练阶段就把$\gamma$去掉的做法。

这是因为不少人认为，深度学习模型之所以“好训”，过参数化有不可忽视的作用，因此贸然去掉已经充分验证的模型的过参数化风险很大。这里的“好训”，主要是指梯度下降这种理论上容易陷入局部最优的方法居然经常可以找到一个实际表现很好的解，这本身就是一件很不可思议的事情。还有《On the Optimization of Deep Networks: Implicit Acceleration by Overparameterization》等工作，表明过参数化隐式地加速了训练，作用类似于SGD中的动量。

最后，VQ本质上可以理解为一种稀疏训练方案，所以SimVQ所带来的启发和改动，也许还能用于其他稀疏训练模型，比如MoE（Mixture of Experts）。当前的MoE训练方案中，Expert之间的更新也是比较独立的，只有被Router选中的Expert才会更新参数，那么是不是有可能像SimVQ一样，所有的Expert后都接一个共享参数的线性变换，用来提高Expert的利用效率？当然MoE本身跟VQ也有很多不同之处，这还只是个猜测。

小结 #

本文介绍了VQ（Vector Quantization）的另一个训练技巧——SimVQ——只在VQ的编码表多加一个线性变换，无需其他改动，就能达到加速收敛、提升编码利用率、降低重构损失等效果，相当简单有效。

转载到请包括本文地址：https://kexue.fm/archives/10519

更详细的转载事宜请参考：《科学空间FAQ》