变分自编码器(三):这样做为什么能成?
By 苏剑林 | 2018-04-03 | 268930位读者 |话说我觉得我自己最近写文章都喜欢长篇大论了,而且扎堆地来~之前连续写了三篇关于Capsule的介绍,这次轮到VAE了,本文是VAE的第三篇探索,说不准还会有第四篇~不管怎么样,数量不重要,重要的是能把问题都想清楚。尤其是对于VAE这种新奇的建模思维来说,更加值得细细地抠。
这次我们要关心的一个问题是:VAE为什么能成?
估计看VAE的读者都会经历这么几个阶段。第一个阶段是刚读了VAE的介绍,然后云里雾里的,感觉像自编码器又不像自编码器的,反复啃了几遍文字并看了源码之后才知道大概是怎么回事;第二个阶段就是在第一个阶段的基础上,再去细读VAE的原理,诸如隐变量模型、KL散度、变分推断等等,细细看下去,发现虽然折腾来折腾去,最终居然都能看明白了。
这时候读者可能就进入第三个阶段了。在这个阶段中,我们会有诸多疑问,尤其是可行性的疑问:“为什么它这样反复折腾,最终出来模型是可行的?我也有很多想法呀,为什么我的想法就不行?”
前文之要 #
让我们再不厌其烦地回顾一下前面关于VAE的一些原理。
VAE希望通过隐变量分解来描述数据$X$的分布
$$p(x)=\int p(x|z)p(z)dz,\quad p(x,z) = p(x|z)p(z)\tag{1}$$
然后对$p(x|z)$用模型$q(x|z)$拟合,$p(z)$用模型$q(z)$拟合,为了使得模型具有生成能力,$q(z)$定义为标准正态分布。
理论上,我们可以使用边缘概率的最大似然来求解模型:
$$\begin{aligned}q(x|z)=&\mathop{\text{argmax}}_{q(x|z)} \int \tilde{p}(x)\ln\left(\int q(x|z)q(z)dz\right)dx\\
=&\mathop{\text{argmax}}_{q(x|z)} \mathbb{E}_{x\sim\tilde{p}(x)}\left[\ln\left(\int q(x|z)q(z)dz\right)\right]
\end{aligned}\tag{2}$$
但是由于圆括号内的积分没法显式求出来,所以我们只好引入KL散度来观察联合分布的差距,最终目标函数变成了
$$\begin{aligned}\mathcal{L} =&\mathbb{E}_{x\sim \tilde{p}(x)} \left[-\int p(z|x)\ln q(x|z)dz+\int p(z|x)\ln \frac{p(z|x)}{q(z)}dz\right]\\
= &\mathbb{E}_{x\sim \tilde{p}(x)} \left[\mathbb{E}_{z\sim p(z|x)}\big[-\ln q(x|z)\big]+\mathbb{E}_{z\sim p(z|x)}\Big[\ln \frac{p(z|x)}{q(z)}\Big]\right]\end{aligned}\tag{3}$$
通过最小化$\mathcal{L}$来分别找出$p(z|x)$和$q(x|z)$。前一文《变分自编码器(二):从贝叶斯观点出发》也表明$\mathcal{L}$有下界$-\mathbb{E}_{x\sim \tilde{p}(x)}\big[\ln \tilde{p}(x)\big]$,所以比较$\mathcal{L}$与$-\mathbb{E}_{x\sim \tilde{p}(x)}\big[\ln \tilde{p}(x)\big]$的接近程度就可以比较生成器的相对质量。
采样之惑 #
在这部分内容中,我们试图对VAE的原理做细致的追问,以求能回答VAE为什么这样做,最关键的问题是,为什么这样做就可行。
采样一个点就够 #
对于$(3)$式,我们后面是这样处理的:
1、留意到$\mathbb{E}_{z\sim p(z|x)}\Big[\ln \frac{p(z|x)}{q(z)}\Big]$正好是$p(z|x)$和$q(z)$的散度$KL\Big(p(z|x)\Big\Vert q(z)\Big)$,而它们俩都被我们都假设为正态分布,所以这一项可以算出来;
2、$\mathbb{E}_{z\sim p(z|x)}\big[-\ln q(x|z)\big]$这一项我们认为只采样一个就够代表性了,所以这一项变成了$-\ln q(x|z),\, z\sim p(z|x)$。
经过这样的处理,整个loss就可以明确写出来了:
$$\mathcal{L}=\mathbb{E}_{x\sim \tilde{p}(x)} \left[-\ln q(x|z) + KL\Big(p(z|x)\Big\Vert q(z)\Big)\right],\quad z\sim p(z|x)\tag{4}$$
等等,可能有读者看不过眼了:$KL\Big(p(z|x)\Big\Vert q(z)\Big)$事先算出来,相当于是采样了无穷多个点来估算这一项;而$\mathbb{E}_{z\sim p(z|x)}\big[-\ln q(x|z)\big]$却又只采样一个点,大家都是loss的一部分,这样不公平待遇真的好么?
事实上,$\mathbb{E}_{z\sim p(z|x)}\Big[\ln \frac{p(z|x)}{q(z)}\Big]$也可以只采样一个点来算,也就是说,可以通过全体都只采样一个点,将$(3)$式变为
$$\begin{aligned}\mathcal{L} =&\mathbb{E}_{x\sim \tilde{p}(x)} \left[-\ln q(x|z)+\ln \frac{p(z|x)}{q(z)}\right]\\
=&\mathbb{E}_{x\sim \tilde{p}(x)} \Big[-\ln q(x|z)+\ln p(z|x) - \ln q(z)\Big]\,,\quad z\sim p(z|x)
\end{aligned}\tag{5}$$
这个loss虽然跟标准的VAE有所不同,但事实上也能收敛到相似的结果。
为什么一个点就够? #
那么,为什么采样一个点就够了呢?什么情况下才是采样一个点就够?
首先,我举一个“采样一个点不够”的例子,让我们回头看$(2)$式,它其实可以改写成:
$$q(x|z)=\mathop{\text{argmax}}_{q(x|z)} \mathbb{E}_{x\sim\tilde{p}(x)}\Bigg[\ln\Big(\mathbb{E}_{z\sim q(z)}\big[q(x|z)\big]\Big)\Bigg]\tag{6}$$
如果采样一个点就够了,不,这里还是谨慎一点,采样$k$个点吧,那么我们可以写出
$$q(x|z)=\mathop{\text{argmax}}_{q(x|z)} \mathbb{E}_{x\sim\tilde{p}(x)}\Bigg[\ln\left(\frac{1}{k}\sum_{i=1}^k q(x|z_i)\right)\Bigg],\quad z_1,\dots,z_k \sim q(z)\tag{7}$$
然后就可以梯度下降训练了。
然而,这样的策略是不成功的。实际中我们能采样的数目$k$,一般要比每个batch的大小要小,这时候最大化$\ln\left(\frac{1}{k}\sum\limits_{i=1}^k q(x|z_i)\right)$就会陷入一个“资源争夺战”的境地:每次迭代时,一个batch中的各个$x_i$都在争夺$z_1,z_2,\dots,z_k$,谁争夺成功了,$q(x|z)$就大(说白了,哪个$x_i$能找到专属于它的$z_j$,这意味着$z_j$只能生成$x_i$,不能生成其它的,那么$z(x_i|z_j)$就大),但是每个样本都是平等的,采样又是随机的,我们无法预估每次“资源争夺战”的战况。这完全就是一片混战!如果数据集仅仅是mnist,那还好一点,因为mnist的样本具有比较明显的聚类倾向,所以采样数母$k$超过10,那么就够各个$x_i$分了;但如果像人脸、imagenet这些没有明显聚类倾向、类内方差比较大的数据集,各个$z$完全是不够分的,一会$x_i$抢到了$z_j$,一会$x_{i+1}$抢到了$z_j$,训练就直接失败了。
因此,正是这种“僧多粥少”的情况导致上述模型$(7)$训练不成功。可是,为什么VAE那里采样一个点就成功了呢?
一个点确实够了 #
这就得再分析一下我们对$q(x|z)$的想法了,我们称$q(x|z)$为生成模型部分,一般情况下我们假设它为伯努利分布或高斯分布,考虑到伯努利分布应用场景有限,这里只假设它是正态分布,那么
$$q(x|z)=\frac{1}{\prod\limits_{k=1}^D \sqrt{2\pi \sigma_{(k)}^2(z)}}\exp\left(-\frac{1}{2}\left\Vert\frac{x-\mu(z)}{\sigma(z)}\right\Vert^2\right)\tag{8}$$
其中$\mu(z)$是用来计算均值的网络,$\sigma^2(z)$是用来计算方差的网络,很多时候我们会固定方差,那就只剩一个计算均值的网络了。
注意,$q(x|z)$只是一个概率分布,我们从$q(z)$中采样出$z$后,代入$q(x|z)$后得到$q(x|z)$的具体形式,理论上我们还要从$q(x|z)$中再采样一次才得到$x$。但是,我们并没有这样做,我们直接把均值网络$\mu(z)$的结果就当成$x$。而能这样做,表明$q(x|z)$是一个方差很小的正态分布(如果是固定方差的话,则训练前需要调低方差,如果不是正态分布而是伯努利分布的话,则不需要考虑这个问题,它只有一组参数),每次采样的结果几乎都是相同的(都是均值$\mu(z)$),此时$x$和$z$之间“几乎”具有一一对应关系,接近确定的函数$x=\mu(z)$。
而对于后验分布$p(z|x)$中,我们假设了它也是一个正态分布。既然前面说$z$与$x$几乎是一一对应的,那么这个性质同样也适用验分布$p(z|x)$,这就表明后验分布也会是一个方差很小的正态分布(读者也可以自行从mnist的encoder结果来验证这一点),这也就意味着每次从$p(z|x)$中采样的结果几乎都是相同的。既然如此,采样一次跟采样多次也就没有什么差别了,因为每次采样的结果都基本一样呀。所以我们就解释了为什么可以从$(3)$式出发,只采样一个点计算而变成$(4)$式或$(5)$式了。
后验之妙 #
前面我们初步解释了为什么直接在先验分布$q(z)$中采样训练不好,而在后验分布中$p(z|x)$中采样的话一个点就够了。事实上,利用KL散度在隐变量模型中引入后验分布是一个非常神奇的招数。在这部分内容中,我们再整理一下相关内容,并且给出一个运用这个思想的新例子。
后验的先验 #
可能读者会有点逻辑混乱:你说$q(x|z)$和$p(z|x)$最终都是方差很小的正态分布,可那是最终的训练结果而已,在建模的时候,理论上我们不能事先知道$q(x|z)$和$p(z|x)$的方差有多大,那怎么就先去采样一个点了?
我觉得这也是我们对问题的先验认识。当我们决定用某个数据集$X$做VAE时,这个数据集本身就带了很强的约束。比如mnist数据集具有784个像素,事实上它的独立维度远少于784,最明显的,有些边缘像素一直都是0,mnist相对于所有28*28的图像来说,是一个非常小的子集;再比如前几天写的作诗机器人,“唐诗”这个语料集相对于一般的语句来说是一个非常小的子集;甚至我们拿上千个分类的imagenet数据集来看,它也是无穷尽的图像中的一个小子集而已。
这样一来,我们就想着这个数据集$X$是可以投影到一个低维空间(隐变量空间)中,然后让低维空间中的隐变量跟原来的$X$集一一对应。读者或许看出来了:这不就是普通的自编码器嘛?是的,其实意思就是说,在普通的自编码器情况下,我们可以做到隐变量跟原数据集的一一对应(完全一一对应意味着$p(z|x)$和$q(x|z)$的方差为0),那么再引入高斯形式的先验分布$q(z)$后,粗略地看,这只是对隐变量空间做了平移和缩放,所以方差也可以不大。
所以,我们应该是事先猜测出$q(x|z)$和$p(z|x)$的方差很小,并且让模型实现这个估计。说白了,“采样一个”这个操作,是我们对数据和模型的先验认识,是对后验分布的先验,并且我们通过这个先验认识来希望模型能靠近这个先验认识去。
整个思路应该是:
1、有了原始语料集;
2、观察原始语料集,推测可以一一对应某个隐变量空间;
3、通过“采样一个”的方式,让模型去学会这个对应。
这部分内容说得有点凌乱~其实也有种多此一举的感觉,希望读者不要被我搞糊涂了。如果觉得混乱的话,忽视这部分吧~
耿直的IWAE #
接下来的例子称为“重要性加权自编码器(Importance Weighted Autoencoders)”,简写为“IWAE”,它更加干脆、直接地体现出后验分布的妙用,它在某种程度上它还可以看成是VAE的升级版。
IWAE的出发点是$(2)$式,它引入了后验分布对$(2)$式进行了改写
$$\int q(x|z)q(z)dz = \int p(z|x)\frac{q(x|z)q(z)}{p(z|x)}dz=\mathbb{E}_{z\sim p(z|x)}\left[\frac{q(x|z)q(z)}{p(z|x)}\right]\tag{8}$$
这样一来,$(2)$式由从$q(z)$采样变成了从$p(z|x)$中采样。我们前面已经论述了$p(z|x)$方差较小,因此采样几个点就够了:
$$\int q(x|z)q(z)dz = \frac{1}{k}\sum_{i=1}^k \frac{q(x|z_i)q(z_i)}{p(z_i|x)},\quad z_1,\dots,z_k\sim p(z|x)\tag{9}$$
代入$(2)$式得到
$$q(x|z)=\mathop{\text{argmax}}_{q(x|z)} \mathbb{E}_{x\sim\tilde{p}(x)}\Bigg[\ln\left(\frac{1}{k}\sum_{i=1}^k \frac{q(x|z_i)q(z_i)}{p(z_i|x)}\right)\Bigg],\quad z_1,\dots,z_k \sim p(z|x)\tag{10}$$
这就是IWAE。为了对齐$(4),(5)$式,可以将它等价地写成
$$\begin{aligned}&q(x|z) = \mathop{\text{argmin}}_{q(x|z),p(z|x)} \mathcal{L}_k,\\
\mathcal{L}_k = \mathbb{E}_{x\sim\tilde{p}(x)}\Bigg[&-\ln\left(\frac{1}{k}\sum_{i=1}^k \frac{q(x|z_i)q(z_i)}{p(z_i|x)}\right)\Bigg],\quad z_1,\dots,z_k \sim p(z|x)\end{aligned}\tag{11}$$
当$k=1$时,上式正好跟$(5)$式一样,所以从这个角度来看,IWAE是VAE的升级版。
从构造过程来看,在$(8)$式中将$p(z|x)$替换为$z$的任意分布都是可以的,选择$p(z|x)$只是因为它有聚焦性,便于采样。而当$k$足够大时,事实上$p(z|x)$的具体形式已经不重要了。这也就表明,在IWAE中削弱了encoder模型$p(z|x)$的作用,换来了生成模型$q(x|z)$的提升。因为在VAE中,我们假设$p(z|x)$是正态分布,这只是一种容易算的近似,这个近似的合理性,同时也会影响生成模型$q(x|z)$的质量。可以证明,$\mathcal{L}_k$能比$\mathcal{L}$更接近下界$-\mathbb{E}_{x\sim \tilde{p}(x)} \left[\ln \tilde{p}(x)\right]$,所以生成模型的质量会更优。
直觉来讲,就是在IWAE中,$p(z|x)$的近似程度已经不是那么重要了,所以能得到更好的生成模型。不过代价是编码模型的质量就降低了,这也是因为$p(z|x)$的重要性降低了,模型就不会太集中精力训练$p(z|x)$了。所以如果我们是希望获得好的encoder的话,IWAE是不可取的。
还有一个工作《Tighter Variational Bounds are Not Necessarily Better》据说同时了提高了encoder和decoder的质量,不过我还没看懂~
重参之神 #
如果说后验分布的引入成功勾画了VAE的整个蓝图,那么重参数技巧就是那“画龙点睛”的“神来之笔”。
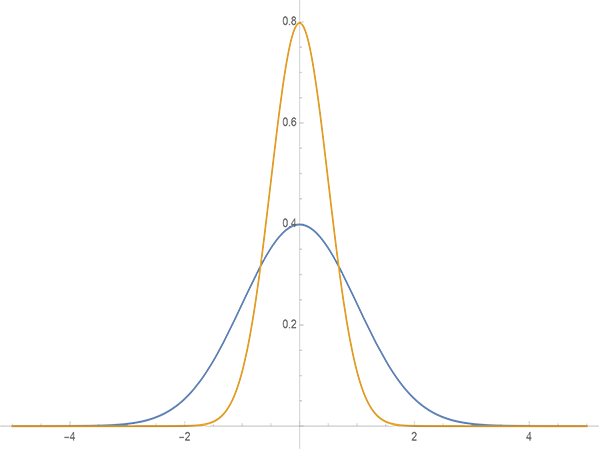
前面我们说,VAE引入后验分布使得采样从宽松的标准正态分布$q(z)$转移到了紧凑的正态分布$p(z|x)$。然而,尽管它们都是正态分布,但是含义却大不一样。我们先写出
$$p(z|x)=\frac{1}{\prod\limits_{k=1}^d \sqrt{2\pi \sigma_{(k)}^2(x)}}\exp\left(-\frac{1}{2}\left\Vert\frac{z-\mu(x)}{\sigma(x)}\right\Vert^2\right)\tag{12}$$
也就是说,$p(z|x)$的均值和方差都是要训练的模型。
让我们想象一下,当模型跑到这一步,然后算出了$\mu(x)$和$\sigma(x)$,接着呢,就可以构建正态分布然后采样了。可采样出来的是什么东西?是一个向量,并且这个向量我们看不出它跟$\mu(x)$和$\sigma(x)$的关系,所以相当于一个常向量,这个向量一求导就没了,从而在梯度下降中,我们无法得到任何反馈来更新$\mu(x)$和$\sigma(x)$。
这时候重参数技巧就闪亮登场了,它直截了当地告诉我们:
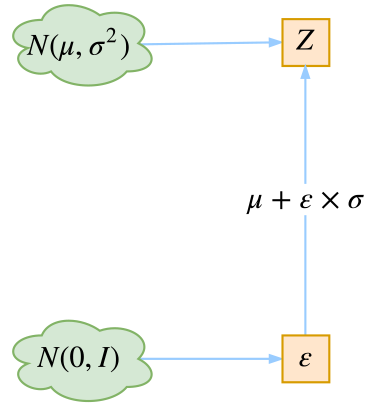
$$z = \mu(x) + \varepsilon \times \sigma(x),\quad \varepsilon\sim \mathcal{N}(0,I).$$
没有比这更简洁了,看起来只是一个微小的变换,但它明确地告诉了我们$z$跟$\mu(x),\sigma(x)$的关系!于是$z$求导就不再是0,$\mu(x),\sigma(x)$终于可以获得属于它们的反馈了。至此,模型一切就绪,接下来就是写代码的时间了~
可见,“重参数”堪称绝杀呀~
本文之水 #
哆里哆嗦,又水了一文~
本文大概是希望把VAE后续的一些小细节说清楚,特别是VAE如何通过巧妙地引入后验分布来解决采样难题(从而解决了训练难题),并且顺道介绍了一下IWAE。
要求直观理解就难免会失去一点严谨性,这是二者不可兼得的事情。所以,对于文章中的毛病,望高手读者多多海涵,也欢迎批评建议~
转载到请包括本文地址:https://kexue.fm/archives/5383
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Apr. 03, 2018). 《变分自编码器(三):这样做为什么能成? 》[Blog post]. Retrieved from https://kexue.fm/archives/5383
@online{kexuefm-5383,
title={变分自编码器(三):这样做为什么能成?},
author={苏剑林},
year={2018},
month={Apr},
url={\url{https://kexue.fm/archives/5383}},
}










March 12th, 2025
您好苏神,本文中您提到一句话“而对于后验分布$p(z|x)$中,我们假设了它也是一个正态分布。既然前面说z与x几乎是一一对应的,那么这个性质同样也适用验分布$p(z|x)$,这就表明后验分布也会是一个方差很小的正态分布”,我有如下两个问题想请教:
1. $p(z|x)$如果是一个方差很小的正态分布,那是否不符合《变分自编码器(二):从贝叶斯观点出发》一文中,“VAE还让所有的$p(Z|X)$都向标准正态分布看齐”这个假设,因为根据式$p(z)=\int p(x,z)dx=\int p(z|x)p(x)dx$可知,如果$p(z|x)$不服从甚至不接近$N(0,I)$分布,那么先验分布$p(z)$一定不符合甚至偏离$N(0,I)$分布,那么后期将VAE作为生成模型时从$N(0,I)$中随机采样放入解码器中就不恰当了;
2. 本文中提到“$q(x|z)$只是一个概率分布,我们从$q(z)$中采样出$z$后,代入$q(x|z)$后得到$q(x|z)$的具体形式,理论上我们还要从$q(x|z)$中再采样一次才得到x。但是,我们并没有这样做,我们直接把均值网络$μ(z)$的结果就当成$x$。而能这样做,表明$q(x|z)$是一个方差很小的正态分布”这句话是否有些自洽?因为并没有解释直接把$μ(z))$作为$x$的理由,而是直接把这个作为先决条件去推测$q(x|z)$以及$p(z|x)$的概率分布形态(小方差)是否有些不合理?
由于本人数学水平并不高明,上述是我思考后提出的两点拙见,希望能得到您的解答,这对我理解VAE原理非常有帮助!谢谢!
1、“VAE还让所有的$p(Z|X)$都向标准正态分布看齐”是方法或者说途径,最终目标实际上是“$p(Z)$都向标准正态分布看齐”;
2、你这样反思也有道理,实际上直接输出$\mu(z)$更多的原因是为了去噪,因为你再采样一次的话,得到的可能会更加逼真,但也更多噪点的图片;
3、但是$p(x|z)$方差小,跟“采样一次”,两者应该是相互促进的结果,就是因为只采样了一次,然后加上重构损失会比KL损失大,所以模型学会了用这个采样一次的结果来重构,于是重构损失小了,KL损失相对就变大了,变大的原因之一就是$p(z|x)$方差小了。