为什么是抛物线?——聚光面研究
By 苏剑林 | 2010-11-07 | 109699位读者 |很多读者都知道,反射望远镜、射电望远镜、太阳能集热器等都有一个抛物状的面,它们都是利用了抛物面能将平行射入的光汇聚到一个点(焦点)上的性质。如果问为什么抛物面具有此性质,相信很多高中生都可以利用抛物线的相关知识来证明。但是,如果反过来问:为什么具有此性质的曲面是抛物面?相信会难倒一部分读者。我们来尝试寻找这一曲线(由于对称的原因,这个曲面可以看作由曲线旋转而成,因此我们可以研究曲线)。
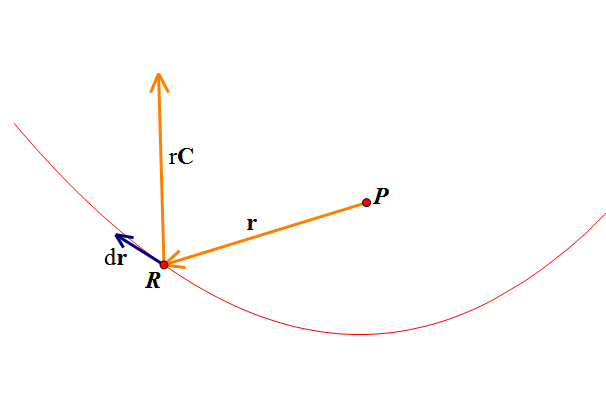
作出如上图的反射示意图,构造一个单位常向量$\vec{C}$(方向固定,$|\vec{C}|=1$),以表示平衡射入的光的方向;并构造从聚光点出发的向量$\vec{r}$,以表示曲线的轨迹,且记$|\vec{r}|=r$。根据“反射角=入射角”,$\vec{r}$、$\vec{C}$与$d\vec{r}$的夹角应当相等。于是有
$\vec{C}\cdot d\vec{r}=\frac{\vec{r}\cdot d\vec{r}}{r}$(考虑等式两边的意义,并联系向量点积的定义和计算就可以推出)
我们有恒等式:$\vec{r}\cdot d\vec{r}=rdr$(注意dr是$d(|\vec{r}|)$而不是$|d\vec{r}|$),代入立马得到
$$\vec{C}\cdot d\vec{r}=dr$$
积分一次,得
$$\vec{C}\cdot \vec{r}=r+K$$
K是常数,如果换回直角坐标系或极坐标系,就可以发现上式是一道抛物线方程。于是问题得解。
在上述讨论中,我们只用到了寥寥几步,这充分体现了向量的巨大好处。BoJone一开始是直接用直角坐标系列方程$dy\sqrt{x^2+y^2}=xdx+ydy$,然后换元为极坐标,尤显麻烦。
此问题提出于一年前,源于爱因斯坦向青少年提出的十大思考问题之“不随太阳移动而移动的太阳炉”。BoJone于2010.11.03作出解答。此题可以说是BoJone列出的首道微分方程,在当时不要说解答了,就连列出这道方程也费了不少功夫。那时候刚刚接触微积分和微分方程,还没有系统地接触向量等知识,仅仅利用薄弱的解析几何知识及各种暴力方法,才列出了方程,最终通过老师来解。还有上篇所提到过的“追牛问题”,也是BoJone比较早接触的微分方程实题之一。对这类问题的初步接触,导致了我对深入研究数学的向往,推动了我去研究数学。
转载到请包括本文地址:https://kexue.fm/archives/1055
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Nov. 07, 2010). 《为什么是抛物线?——聚光面研究 》[Blog post]. Retrieved from https://kexue.fm/archives/1055
@online{kexuefm-1055,
title={为什么是抛物线?——聚光面研究},
author={苏剑林},
year={2010},
month={Nov},
url={\url{https://kexue.fm/archives/1055}},
}











November 8th, 2010
我有个小疑问:文中的恒等式是如何得到的呢?
现在我想通了,原来$dr$是$d\vec{r}$在$\vec{r}$方向的分量的大小。
实际上还可以换回直角坐标系推导这一恒等式
November 8th, 2010
我觉得想到这种方法很不容易。我看了半天才明白
实际上任何新东西在上手之初都会比较困难,慢慢熟悉了就可以了
November 9th, 2010
由此看来,向量真是一个神奇的数学工具。
November 25th, 2010
...我表示压力很大...微积分哈...表示对其九窍通了八窍...学啊...
November 27th, 2010
站长您好!我想给您提一个合理化建议:http://bbs.spaces.ac.cn/viewtopic.php?id=26;
此外,我想了解白纸上一条直线在柱面镜成什么像,您有没有可帮助我的资料呢?谢谢!
谢谢你的建议,有时间我会对天文奥赛网进行一定的修改的。
April 10th, 2013
抛物面能将平行射入的光汇聚到一个点
不准确吧,彗差呢?
彗差是不是在折射透镜才出现的?
另一方面,这里考虑的当然只是光的粒子说...
如果物点不在主光轴应该会有彗差吧。。。
如果考虑波动的话,还要干涉什么的。。。
我知道了,平行光通过抛物镜可以汇聚成一点,但是不同角度来的平衡光却汇聚成不同的点,所以就产生了彗差。这个问题只能通过改正镜来解决了,当然增加焦距可以减少这个效应吧。
May 30th, 2013
我有一个极其简单,显然的证明
May 25th, 2014
爱因斯坦向青少年提出的十大思考问题 这个是什么呢
在爱因斯坦写的那本《相对论》中有(亚马逊搜索“相对论”第一本就是,作者就是爱因斯坦),那些问题可能不是完全由爱因斯坦提出来的)。这些问题包括:不随太阳移动的太阳灶、彩色的影子等等。