生成扩散模型漫谈（十六）：W距离 ≤ 得分匹配

Wasserstein距离（下面简称“W距离”），是基于最优传输思想来度量两个概率分布差异程度的距离函数，笔者之前在《从Wasserstein距离、对偶理论到WGAN》等博文中也做过介绍。对于很多读者来说，第一次听说W距离，是因为2017年出世的WGAN，它开创了从最优传输视角来理解GAN的新分支，也提高了最优传输理论在机器学习中的地位。很长一段时间以来，GAN都是生成模型领域的“主力军”，直到最近这两年扩散模型异军突起，GAN的风头才有所下降，但其本身仍不失为一个强大的生成模型。

从形式上来看，扩散模型和GAN差异很明显，所以其研究一直都相对独立。不过，去年底的一篇论文《Score-based Generative Modeling Secretly Minimizes the Wasserstein Distance》打破了这个隔阂：它证明了扩散模型的得分匹配损失可以写成W距离的上界形式。这意味着在某种程度上，最小化扩散模型的损失函数，实则跟WGAN一样，都是在最小化两个分布的W距离。

结论分析 #

具体来说，原论文的结果，是针对《生成扩散模型漫谈（五）：一般框架之SDE篇》中介绍的SDE式扩散模型的，其核心结论是不等式（其中$I_t$是$t$的非负函数，具体含义我们后来再详细介绍）
\begin{equation}\mathcal{W}_2[p_0,q_0]\leq \int_0^T g_t^2 I_t \left(\mathbb{E}_{\boldsymbol{x}_t\sim p_t(\boldsymbol{x}_t)}\left[\left\Vert\nabla_{\boldsymbol{x}_t}\log p(\boldsymbol{x}_t) - \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)\right\Vert^2\right]\right)^{1/2}dt + I_T \mathcal{W}_2[p_T,q_T]\label{eq:w-neq}\end{equation}
那么怎样理解这个不等式呢？首先，扩散模型可以理解为SDE从$t=T$到$t=0$的一个运动过程，最右边的$p_T,q_T$是$T$时刻的随机采样分布，$p_T$通常就是标准正态分布，而实际应用中一般都有$q_T = p_T$，所以$\mathcal{W}_2[p_T,q_T]=0$，原论文之所以显式写出它，只是为了从理论上给出最一般的结果。

接着，左边的$p_0$，是从$p_T$采样的随机点出发，经反向SDE
\begin{equation}d\boldsymbol{x}_t = \left[\boldsymbol{f}_t(\boldsymbol{x}_t) - g_t^2\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t) \right] dt + g_t d\boldsymbol{w}\label{eq:reverse-sde}\end{equation}
求解得到的$t=0$时刻的值的分布，它实际上就是要生成的数据分布；而$q_0$，则是从$q_T$采样的随机点出发，经过SDE
\begin{equation}d\boldsymbol{x}_t = \left[\boldsymbol{f}_t(\boldsymbol{x}_t) - g_t^2\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t) \right] dt + g_t d\boldsymbol{w}\end{equation}
求解得到的$t=0$时刻的值的分布，其中$\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)$是$\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t)$的神经网络近似，所以$q_0$实际就是扩散模型生成的数据分布。因此，$\mathcal{W}_2[p_0,q_0]$的含义就是数据分布与生成分布的W距离。

最后，剩下的积分项，其关键部分是
\begin{equation}\mathbb{E}_{\boldsymbol{x}_t\sim p_t(\boldsymbol{x}_t)}\left[\left\Vert\nabla_{\boldsymbol{x}_t}\log p(\boldsymbol{x}_t) - \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)\right\Vert^2\right]\label{eq:sm}\end{equation}
这也正好是扩散模型的“得分匹配”损失。所以，当我们用得分匹配损失去训练扩散模型的时候，其实也间接地最小化了数据分布与生成分布的W距离。跟WGAN不同的是，WGAN优化的W距离是$\mathcal{W}_1[p_0,q_0]$而这里是$\mathcal{W}_2[p_0,q_0]$。

注：准确来说，式$\eqref{eq:sm}$还不是扩散模型的损失函数，扩散模型的损失函数应该是“条件得分匹配”，它跟得分匹配的关系是：
\begin{equation}\begin{aligned}
&\,\mathbb{E}_{\boldsymbol{x}_t\sim p_t(\boldsymbol{x}_t)}\left[\left\Vert\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t) - \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)\right\Vert^2\right] \\
=&\,\mathbb{E}_{\boldsymbol{x}_t\sim p_t(\boldsymbol{x}_t)}\left[\left\Vert\mathbb{E}_{\boldsymbol{x}_0\sim p_t(\boldsymbol{x}_0|\boldsymbol{x}_t)}\left[\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t|\boldsymbol{x}_0)\right] - \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)\right\Vert^2\right] \\
\leq &\,\mathbb{E}_{\boldsymbol{x}_t\sim p_t(\boldsymbol{x}_t)}\mathbb{E}_{\boldsymbol{x}_0\sim p_t(\boldsymbol{x}_0|\boldsymbol{x}_t)}\left[\left\Vert\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t|\boldsymbol{x}_0) - \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)\right\Vert^2\right] \\
= &\,\mathbb{E}_{\boldsymbol{x}_0\sim p_0(\boldsymbol{x}_0),\boldsymbol{x}_t\sim p_t(\boldsymbol{x}_t|\boldsymbol{x}_0)}\left[\left\Vert\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t|\boldsymbol{x}_0) - \boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)\right\Vert^2\right] \\
\end{aligned}\end{equation}
最后的结果才是扩散模型的损失函数“条件得分匹配”。第一个等号是因为恒等式$\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t)=\mathbb{E}_{\boldsymbol{x}_0\sim p_t(\boldsymbol{x}_0|\boldsymbol{x}_t)}\left[\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t|\boldsymbol{x}_0)\right]$，第二个不等号则是因为平方平均不等式的推广或者詹森不等式，第三个等号则是贝叶斯公式了。也就是说，条件得分匹配是得分匹配的上界，所以也是W距离的上界。

从式$\eqref{eq:w-neq}$中我们也可以简单理解为什么扩散模型的目标函数要舍去模长前面的系数了，因为W距离是概率分布的良好度量，而式$\eqref{eq:w-neq}$右端的$g_t^2 I_t$是关于$t$的单调递增函数，这意味着我们要适当加大当$t$较小时的得分匹配损失。而在《生成扩散模型漫谈（五）：一般框架之SDE篇》我们推导过得到匹配的最终形式为：
\begin{equation}\frac{1}{\bar{\beta}_t^2}\mathbb{E}_{\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0),\boldsymbol{\varepsilon}\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{I})}\left[\left\Vert \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\bar{\alpha}_t\boldsymbol{x}_0 + \bar{\beta}_t\boldsymbol{\varepsilon}, t) - \boldsymbol{\varepsilon}\right\Vert^2\right]\end{equation}
舍去系数$\frac{1}{\bar{\beta}_t^2}$等价于乘以$\bar{\beta}_t^2$，而$\bar{\beta}_t^2$也是$t$的单调递增函数。也就是说，可以简单地认为舍去系数是让训练目标更加接近两个分布的W距离。

准备工作 #

尽管原论文给出了不等式$\eqref{eq:w-neq}$的证明过程，但涉及到较多的最优传输相关知识，如连续性方程、梯度流等，特别是它不加证明引用的一个定理，还是放在一本梯度流专著的第8章或另一本最优传输专著的第5章，这对笔者来说阅读难度实在太大。经过一段时间的尝试，笔者终于在上周笔者完成了自己关于不等式$\eqref{eq:w-neq}$的（一部分）证明，其中只需要用到W距离的定义、微分方程基础以及柯西不等式，相比原论文的证明理解难度应该是明显降低了。经过几天的修改完善，给出如下的证明过程。

在开始证明之前，我们先做一下准备，先整理一下接下来会用到的一些基本概念和结论。首先是W距离，它定义为
\begin{equation}\mathcal{W}_{\rho}[p,q]=\left(\inf_{\gamma\in \Pi[p,q]} \iint \gamma(\boldsymbol{x},\boldsymbol{y}) \Vert\boldsymbol{x} - \boldsymbol{y}\Vert^{\rho} d\boldsymbol{x}d\boldsymbol{y}\right)^{1/\rho}\end{equation}
其中$\Pi[p,q]$是指所有以$p,q$为边缘分布的联合概率密度函数，它描述了具体的传输方案。本文只考虑$\rho=2$，因为只有这种情形方便后续推导。注意到W距离的定义包含了下确界运算$\inf$，这就意味着对于任意我们能写出的$\gamma\in \Pi[p,q]$，都有
\begin{equation}\mathcal{W}_2[p,q]\leq\left(\iint \gamma(\boldsymbol{x},\boldsymbol{y}) \Vert\boldsymbol{x} - \boldsymbol{y}\Vert^{2} d\boldsymbol{x}d\boldsymbol{y}\right)^{1/2}\label{eq:core-neq}\end{equation}
这是笔者所给证明的核心思想。证明过程的放缩，主要用到柯西不等式：
\begin{equation}\begin{aligned}
&\text{向量版：}\quad\boldsymbol{x}\cdot\boldsymbol{y}\leq \Vert \boldsymbol{x}\Vert \Vert\boldsymbol{y}\Vert\\
&\text{期望版：}\quad\mathbb{E}_{\boldsymbol{x}}\left[f(\boldsymbol{x})g(\boldsymbol{x})\right]\leq \left(\mathbb{E}_{\boldsymbol{x}}\left[f^2(\boldsymbol{x})\right]\right)^{1/2}\left(\mathbb{E}_{\boldsymbol{x}}\left[g^2(\boldsymbol{x})\right]\right)^{1/2}
\end{aligned}\end{equation}
证明过程中我们会假设函数$\boldsymbol{g}_t(\boldsymbol{x})$满足“单侧Lipschitz约束”，其定义为
\begin{equation}(\boldsymbol{g}_t(\boldsymbol{x}) - \boldsymbol{g}_t(\boldsymbol{y}))\cdot(\boldsymbol{x} - \boldsymbol{y}) \leq L_t \Vert \boldsymbol{x} - \boldsymbol{y}\Vert^2\label{eq:assum}\end{equation}
可以证明它比常见的Lipschitz约束（参考《深度学习中的Lipschitz约束：泛化与生成模型》）更弱，即如果函数$\boldsymbol{g}_t(\boldsymbol{x})$满足Lipschitz约束，那么它一定满足单侧Lipschitz约束。

牛刀小试 #

不等式$\eqref{eq:w-neq}$过于一般了，一上来就试图分析一般化的结果并不利于我们的思考和理解。所以，我们先将问题简化一下，看能不能先证明一个稍弱一些的结果。怎么简化呢？首先，不等式$\eqref{eq:w-neq}$考虑了初始分布（提示，扩散模型是$t=T$到$t=0$的演化过程，所以$t=T$是初始时刻，$t=0$是终止时刻）的差异，而这里我们先考虑相同初始分布；此外，原本的反向方程$\eqref{eq:reverse-sde}$是一个SDE，这里先考虑确定性的ODE。

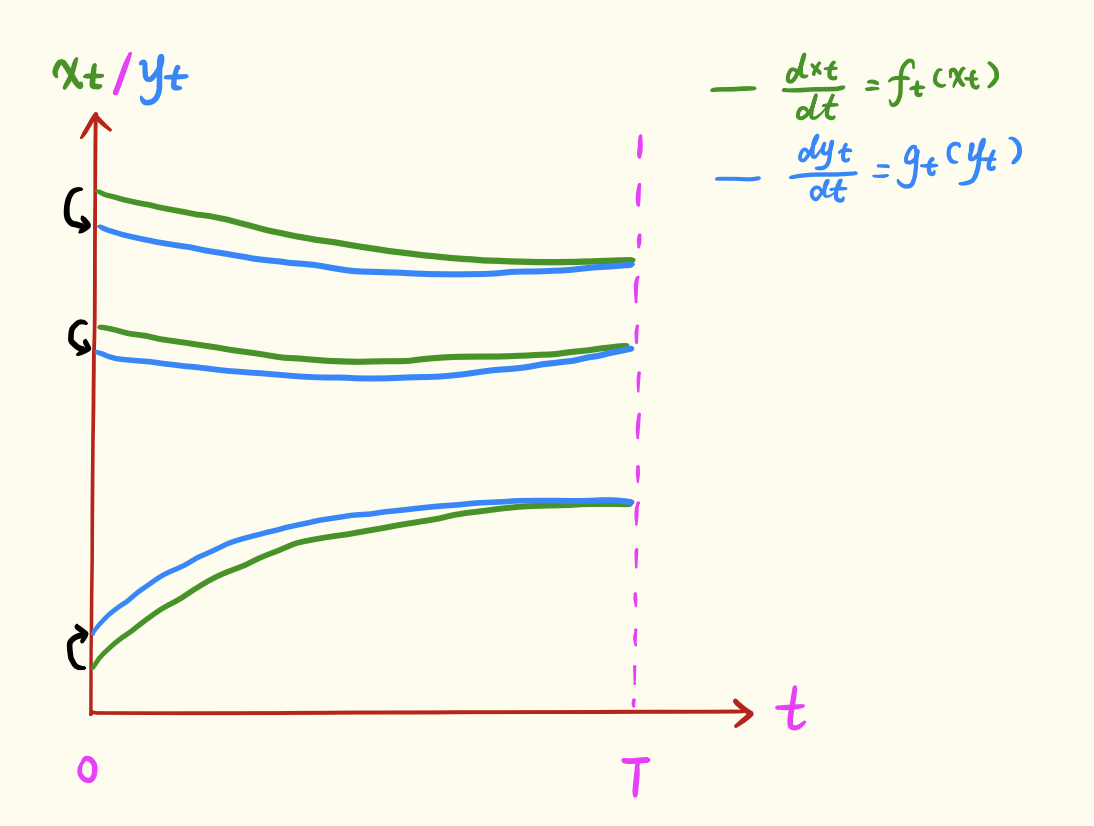
具体来说，我们考虑从同一个分布$q(\boldsymbol{z})$出发采样$\boldsymbol{z}$作为$T$时刻的初始值，然后分别沿着两个不同的ODE
\begin{equation}\frac{d\boldsymbol{x}_t}{dt} = \boldsymbol{f}_t(\boldsymbol{x}_t),\quad \frac{d\boldsymbol{y}_t}{dt} = \boldsymbol{g}_t(\boldsymbol{y}_t)\end{equation}
进行演化，设$t$时刻$\boldsymbol{x}_t$的分布为$p_t$、$\boldsymbol{y}_t$的分布为$q_t$，我们尝试去估计$\mathcal{W}_2[p_0,q_0]$的一个上界。

我们知道，$\boldsymbol{x}_t,\boldsymbol{y}_t$都是以$\boldsymbol{z}$为初始值通过各自的ODE演化而来，所以它们其实都是$\boldsymbol{z}$的确定性函数，更准确的记号应该是$\boldsymbol{x}_t(\boldsymbol{z}),\boldsymbol{y}_t(\boldsymbol{z})$，简单起见我们才略去了$\boldsymbol{z}$。这就意味着对应于同一个$\boldsymbol{x}$的$\boldsymbol{x}_t\leftrightarrow \boldsymbol{y}_t$构成了$p_t,q_t$的样本之间的一个对应关系（传输方案），如下图（这个图不大好画，就随便手画了一下）：

近似最优传输方案示意图

其中第一个不等号用到了柯西不等式的向量版，以及单侧Lipschitz约束假设$\eqref{eq:assum}$，第二个不等号则用到了柯西不等式的期望版，$\pm$的意思是最终得到的不等关系，不管取$+$还是$-$都是成立的，下面的推导只用到了$-$这一侧。结合$\left(w^2\right)'=2ww'$，我们得到
\begin{equation}-\frac{d\tilde{\mathcal{W}}_2[p_t,q_t]}{dt} \leq \left(\mathbb{E}_{\boldsymbol{z}}\left[\Vert\boldsymbol{f}_t(\boldsymbol{x}_t) - \boldsymbol{g}_t(\boldsymbol{x}_t)\Vert^2\right]\right)^{1/2} + L_t\tilde{\mathcal{W}}_2[p_t,q_t] \label{eq:der-neq-1}\end{equation}
用常数变易法，设$\tilde{\mathcal{W}}_2[p_t,q_t]=C_t \exp\left(\int_t^T L_s ds\right)$，代入上式得到
\begin{equation}-\frac{dC_t}{dt} \leq \exp\left(-\int_t^T L_s ds\right)\left(\mathbb{E}_{\boldsymbol{z}}\left[\Vert\boldsymbol{f}_t(\boldsymbol{x}_t) - \boldsymbol{g}_t(\boldsymbol{x}_t)\Vert^2\right]\right)^{1/2}\label{eq:der-neq-2}\end{equation}
两边在$[0,T]$积分，并结合$C_T=0$（初始时刻两个分布相等，距离为0），得到
\begin{equation}C_0 \leq \int_0^T \exp\left(-\int_t^T L_s ds\right)\left(\mathbb{E}_{\boldsymbol{z}}\left[\Vert\boldsymbol{f}_t(\boldsymbol{x}_t) - \boldsymbol{g}_t(\boldsymbol{x}_t)\Vert^2\right]\right)^{1/2} dt\end{equation}
于是
\begin{equation}\tilde{\mathcal{W}}_2[p_0,q_0] \leq C_0 \exp\left(\int_0^T L_s ds\right) =\int_0^T I_t\left(\mathbb{E}_{\boldsymbol{z}}\left[\Vert\boldsymbol{f}_t(\boldsymbol{x}_t) - \boldsymbol{g}_t(\boldsymbol{x}_t)\Vert^2\right]\right)^{1/2} dt\end{equation}
其中$I_t = \exp\left(\int_0^t L_s ds\right)$。根据式$\eqref{eq:core-neq-2}$，这也是$\mathcal{W}_2[p_0,q_0]$的上界。最后，由于求期望的式子只是$\boldsymbol{x}_t$的函数，$\boldsymbol{x}_t$又是$\boldsymbol{z}$的确定性函数，对于它关于$\boldsymbol{z}$的期望等价于直接关于$\boldsymbol{x}_t$的期望，于是：
\begin{equation}\mathcal{W}_2[p_0,q_0] \leq\int_0^T I_t\left(\mathbb{E}_{\boldsymbol{x}_t\sim p_t(\boldsymbol{x}_t)}\left[\Vert\boldsymbol{f}_t(\boldsymbol{x}_t) - \boldsymbol{g}_t(\boldsymbol{x}_t)\Vert^2\right]\right)^{1/2} dt\label{eq:w-neq-0}\end{equation}

一鼓作气 #

实际上，简化版的不等式$\eqref{eq:w-neq-0}$已经和更一般的$\eqref{eq:w-neq}$没有本质区别了，它的推导过程已经包含了导出完整结果的一般思路，下面我们来完成剩余的推导过程。

首先，我们将式$\eqref{eq:w-neq-0}$推广到不同初始分布的场景，假设两个初始分布为$p_T(\boldsymbol{z}_1),q_T(\boldsymbol{z}_2)$，从$p_T(\boldsymbol{z}_1)$采样初始值演化$\boldsymbol{x}_t$，从$q_T(\boldsymbol{z}_2)$采样初始值演化$\boldsymbol{y}_t$，所以此时$\boldsymbol{x}_t,\boldsymbol{y}_t$分别是$\boldsymbol{z}_1,\boldsymbol{z}_2$的函数，而不是像之前那样是同一个$\boldsymbol{z}$的函数，所以无法直接构造一个传输方案。所以，我们还需要$\boldsymbol{z}_1,\boldsymbol{z}_2$之间的一个对应关系（传输方案），我们将它选择为$p_T(\boldsymbol{z}_1),q_T(\boldsymbol{z}_2)$之间的一个最优传输方案$\gamma^*(\boldsymbol{z}_1,\boldsymbol{z}_2)$。于是，我们可以写出类似式$\eqref{eq:core-neq-2}$的结果：
\begin{equation}\mathcal{W}_2^2[p_t,q_t]\leq \mathbb{E}_{\boldsymbol{z}_1,\boldsymbol{z}_2\sim \gamma^*(\boldsymbol{z}_1,\boldsymbol{z}_2)}\left[\Vert\boldsymbol{x}_t - \boldsymbol{y}_t\Vert^{2} \right]\triangleq \tilde{\mathcal{W}}_2^2[p_t,q_t]\label{eq:core-neq-3}\end{equation}
由于定义的一致性，那么放缩过程$\eqref{eq:der-neq-0}$同样是成立的，只不过期望$\mathbb{E}_{\boldsymbol{z}}$换成了$\mathbb{E}_{\boldsymbol{z}_1,\boldsymbol{z}_2}$，所以不等式$\eqref{eq:der-neq-1}$、$\eqref{eq:der-neq-2}$也是成立的。不同的是在对$\eqref{eq:der-neq-2}$两端在$[0,T]$积分时，不再有$C_T = 0$，而是根据定义有$C_T=\tilde{\mathcal{W}}_2[p_T,q_T]=\mathcal{W}_2[p_T,q_T]$。所以，最终的结果是
\begin{equation}\mathcal{W}_2[p_0,q_0] \leq\int_0^T I_t\left(\mathbb{E}_{\boldsymbol{x}_t\sim p_t(\boldsymbol{x}_t)}\left[\Vert\boldsymbol{f}_t(\boldsymbol{x}_t) - \boldsymbol{g}_t(\boldsymbol{x}_t)\Vert^2\right]\right)^{1/2} dt + I_T \mathcal{W}_2[p_T,q_T]\label{eq:w-neq-1}\end{equation}

最后，我们回到扩散模型。在《生成扩散模型漫谈（六）：一般框架之ODE篇》我们已经推导过，同一个前向扩散过程，实际上对应一簇反向过程：
\begin{equation}d\boldsymbol{x} = \left(\boldsymbol{f}_t(\boldsymbol{x}) - \frac{1}{2}(g_t^2 + \sigma_t^2)\nabla_{\boldsymbol{x}}\log p_t(\boldsymbol{x})\right) dt + \sigma_t d\boldsymbol{w}\label{eq:sde-reverse-2}\end{equation}
其中$\sigma_t$是可以自由选择的标准差函数，当$\sigma_t=g_t$时，那么就是方程$\eqref{eq:reverse-sde}$。由于我们上面分析的是ODE，所以我们先考虑$\sigma_t=0$的情形，此时结果$\eqref{eq:w-neq-1}$依然可用，只不过将$\boldsymbol{f}_t(\boldsymbol{x}_t)$换成$\boldsymbol{f}_t(\boldsymbol{x}_t) - \frac{1}{2}g_t^2\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t)$、将$\boldsymbol{g}_t(\boldsymbol{x}_t)$换成$\boldsymbol{f}_t(\boldsymbol{x}_t) - \frac{1}{2}g_t^2\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)$，代入式$\eqref{eq:w-neq-1}$后就得到文章开头的结论$\eqref{eq:w-neq}$了。当然别忘了我们推导过程中对$\boldsymbol{g}_t(\boldsymbol{x}_t)$所做的单侧Lipschitz约束假设$\eqref{eq:assum}$，现在可以分别对$\boldsymbol{f}_t(\boldsymbol{x}_t)$、$\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}_t,t)$做出假设，这些细节就不展开了。

艰难收尾 #

按照流程，接下来我们应该再接再厉，完成$\sigma_t\neq 0$的收尾证明。不过很遗憾，本文的思路不能完全证明SDE的情形，下面给出笔者的分析过程。事实上，对于大部分读者来说，了解到上一节的ODE例子就可以窥见式$\eqref{eq:w-neq-1}$的精髓了，完整的细节也不是太重要。

简单起见，下面我们以$\eqref{eq:reverse-sde}$为例，更一般的$\eqref{eq:sde-reverse-2}$也可以类似地分析。我们需要估算的是如下两个SDE的演化轨迹分布差异：
\begin{equation}\left\{\begin{aligned}
d\boldsymbol{x}_t =&\, \left[\boldsymbol{f}_t(\boldsymbol{x}_t) - g_t^2\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t) \right] dt + g_t d\boldsymbol{w}\\[5pt]
d\boldsymbol{y}_t =&\, \left[\boldsymbol{f}_t(\boldsymbol{y}_t) - g_t^2\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{y}_t,t) \right] dt + g_t d\boldsymbol{w}
\end{aligned}\right.\end{equation}
也就是将准确的$\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t)$换成近似的$\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{y}_t,t)$，对最终分布的影响有多大。笔者的证明思路同样是将它转化为ODE，继而用回前面的证明过程。首先，根据式$\eqref{eq:sde-reverse-2}$，我们知道第一个SDE对应的ODE为：
\begin{equation}
d\boldsymbol{x}_t = \left[\boldsymbol{f}_t(\boldsymbol{x}_t) - g_t^2\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t) \right] dt + g_t d\boldsymbol{w}\\
\Downarrow \\
d\boldsymbol{x}_t = \left[\boldsymbol{f}_t(\boldsymbol{x}_t) - \frac{1}{2}g_t^2\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t) \right] dt
\end{equation}
至于第二个SDE对应的ODE的推导有些技巧，需要先变为$-g_t^2\nabla_{\boldsymbol{y}_t}\log q_t(\boldsymbol{y}_t)$的形式，然后再利用式$\eqref{eq:sde-reverse-2}$：
\begin{equation}
d\boldsymbol{y}_t = \left[\boldsymbol{f}_t(\boldsymbol{y}_t) - g_t^2\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{y}_t,t) \right] dt + g_t d\boldsymbol{w} \\
\Downarrow \\
d\boldsymbol{y}_t = \Big[\underbrace{\boldsymbol{f}_t(\boldsymbol{y}_t) - g_t^2\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{y}_t,t) + g_t^2\nabla_{\boldsymbol{y}_t}\log q_t(\boldsymbol{y}_t)}_{\text{看成整体}} - g_t^2\nabla_{\boldsymbol{y}_t}\log q_t(\boldsymbol{y}_t) \Big] dt + g_t d\boldsymbol{w} \\
\Downarrow \\
d\boldsymbol{y}_t = \left[\boldsymbol{f}_t(\boldsymbol{y}_t) - g_t^2\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{y}_t,t) + g_t^2\nabla_{\boldsymbol{y}_t}\log q_t(\boldsymbol{y}_t) - \frac{1}{2}g_t^2\nabla_{\boldsymbol{y}_t}\log q_t(\boldsymbol{y}_t) \right] dt \\
\Downarrow \\
d\boldsymbol{y}_t = \left[\boldsymbol{f}_t(\boldsymbol{y}_t) - g_t^2\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{y}_t,t) + \frac{1}{2}g_t^2\nabla_{\boldsymbol{y}_t}\log q_t(\boldsymbol{y}_t)\right] dt
\end{equation}
对这两个ODE重复放缩过程$\eqref{eq:der-neq-0}$（$\pm$取负号），那么主要的区别是多出来一项
\begin{equation}-\frac{1}{2}g_t^2\mathbb{E}_{\boldsymbol{z}}\left[(\boldsymbol{x}_t - \boldsymbol{y}_t)\cdot (\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t)-\nabla_{\boldsymbol{y}_t}\log q_t(\boldsymbol{y}_t))\right]\end{equation}
如果这一项小于等于0，那么放缩过程$\eqref{eq:der-neq-0}$依然成立，后面的所有结果同样也成立，最终结论的形式跟式$\eqref{eq:w-neq-1}$一致。

所以，现在剩下的问题就是能否证明
\begin{equation}\mathbb{E}_{\boldsymbol{z}}\left[(\boldsymbol{x}_t - \boldsymbol{y}_t)\cdot (\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t)-\nabla_{\boldsymbol{y}_t}\log q_t(\boldsymbol{y}_t))\right]\geq 0\end{equation}
很遗憾，可以举出反例表明它一般是不成立的。原论文的证明过程也出现了类似的一项，不过求期望的分布不是$\boldsymbol{z}$，而是$\boldsymbol{x}_t,\boldsymbol{y}_t$的最优传输分布，在此前提之下，原论文直接抛出两篇文献的结论作为引理，寥寥几行便完成了证明。不得不说原论文作者们真的很熟悉最优传输相关内容，各种文献结论“信手拈来”，就是苦了笔者这样的新手读者，想要彻底理解却难以下手，只能到此为止了。

特别注意的是，我们不能对$\nabla_{\boldsymbol{x}_t}\log p_t(\boldsymbol{x}_t)$或$\nabla_{\boldsymbol{y}_t}\log q_t(\boldsymbol{y}_t)$做单侧Lipschitz约束假设，因为很容易举出其对数梯度不满足单侧Lipschitz约束的分布，因此，要证明这个不等式，只能参考原论文的思路通过分布本身的性质来进行，不能强加额外的假设。

文章小结 #

本文介绍了一个新的理论结果，显示扩散模型的得分匹配损失可以写成W距离的上界形式，并给出了自己的部分证明。这个结果意味着，在某种程度上扩散模型和WGAN都有着相同的优化目标，扩散模型也在偷偷优化W距离！

转载到请包括本文地址：https://kexue.fm/archives/9467

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。