语言模型输出端共享Embedding的重新探索

预训练刚兴起时，在语言模型的输出端重用Embedding权重是很常见的操作，比如BERT、第一版的T5、早期的GPT，都使用了这个操作，这是因为当模型主干部分不大且词表很大时，Embedding层的参数量很可观，如果输出端再新增一个独立的同样大小的权重矩阵的话，会导致显存消耗的激增。不过随着模型参数规模的增大，Embedding层的占比相对变小了，加之《Rethinking embedding coupling in pre-trained language models》等研究表明共享Embedding可能会有些负面影响，所以现在共享Embedding的做法已经越来越少了。

本文旨在分析在共享Embedding权重时可能遇到的问题，并探索如何更有效地进行初始化和参数化。尽管共享Embedding看起来已经“过时”，但这依然不失为一道有趣的研究题目。

共享权重 #

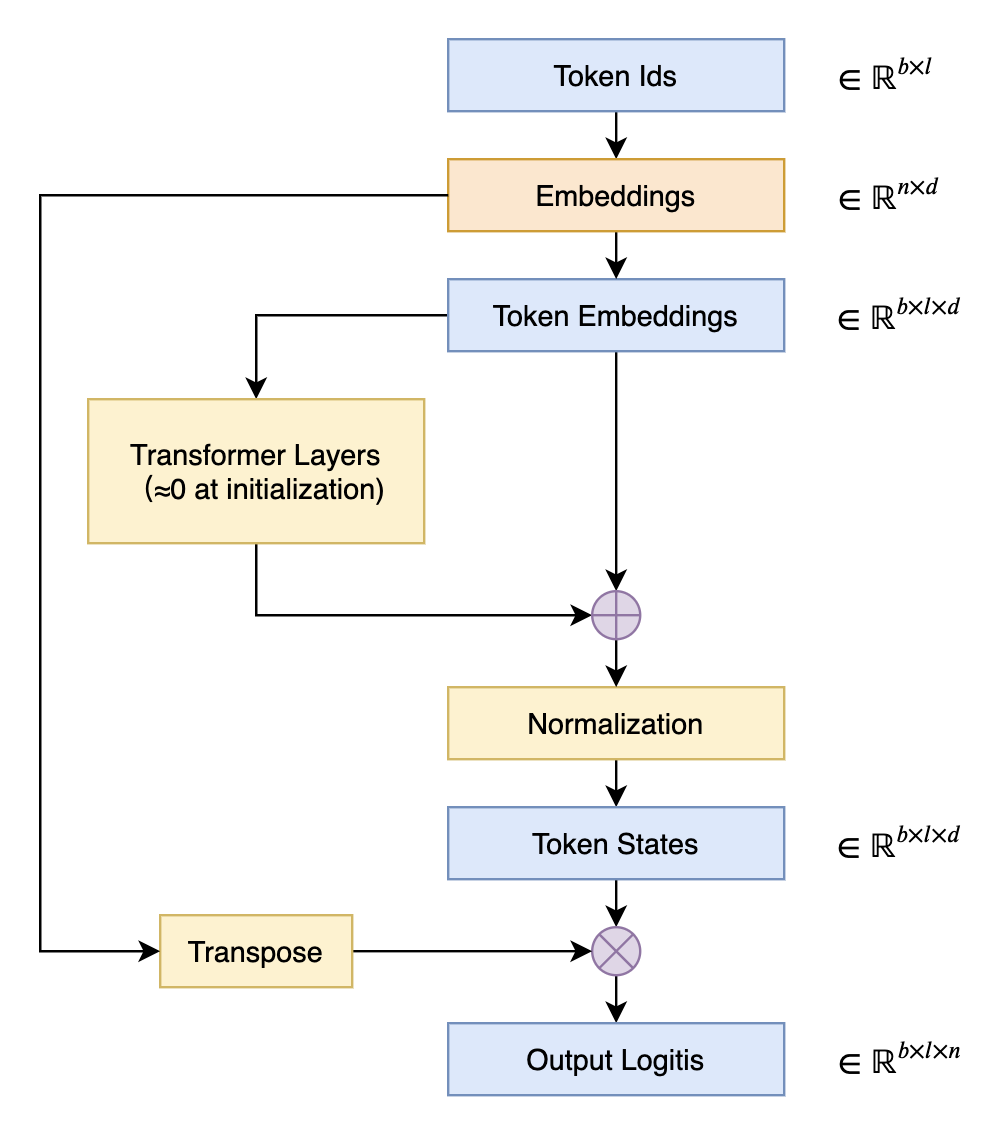
在语言模型的输出端重用Embedding权重的做法，英文称之为“Tied Embeddings”或者“Coupled Embeddings”，其思想主要是Embedding矩阵跟输出端转换到logits的投影矩阵大小是相同的（只差个转置），并且由于这个参数矩阵比较大，所以为了避免不必要的浪费，干脆共用同一个权重，如下图所示：

共享Embedding最直接的后果可能是——它会导致预训练的初始损失非常大。这是因为我们通常会使用类似DeepNorm的技术来降低训练难度，它们都是将模型的残差分支初始化得接近于零。换言之，模型在初始阶段近似于一个恒等函数，这使得初始模型相当于共享Embedding的2-gram模型。接下来我们将推导这样的2-gram模型损失大的原因，以及分析一些解决方案。

准备工作 #

在正式开始推导之前，我们需要准备一些基础结论。

首先，要明确的是，我们主要对初始阶段的结果进行分析，此时的权重都是从某个“均值为0、方差为$\sigma^2$”的分布中独立同分布地采样出来的，这允许我们通过期望来估计某些求和结果。比如对于$\boldsymbol{w}=(w_1,w_2,\cdots,w_d)$，我们有
\begin{equation}\mathbb{E}\left[\Vert \boldsymbol{w}\Vert^2\right] = \mathbb{E}\left[\sum_i w_i^2\right] = \sum_i \mathbb{E}\left[w_i^2\right] = d\sigma^2\label{eq:norm}\end{equation}
因此可以取$\Vert \boldsymbol{w}\Vert\approx \sqrt{d}\sigma$。那么误差有多大呢？我们可以通过它的方差来感知。为此，我们先求它的二阶矩：
\begin{equation}\begin{aligned}\mathbb{E}\left[\Vert \boldsymbol{w}\Vert^4\right] =&\, \mathbb{E}\left[\left(\sum_i w_i^2\right)^2\right] = \mathbb{E}\left[\sum_i w_i^4 + \sum_{i,j|i\neq j} w_i^2 w_j^2\right] \\
=&\, \sum_i \mathbb{E}\left[w_i^4\right] + \sum_{i,j|i\neq j} \mathbb{E}\left[w_i^2\right] \mathbb{E}\left[w_j^2\right] \\
=&\, d\,\mathbb{E}\left[w^4\right] + d(d-1) \sigma^4 \\
\end{aligned}\end{equation}
如果采样分布是正态分布，那么可以直接算出$\mathbb{E}\left[w^4\right]=3\sigma^4$，所以
\begin{equation}\mathbb{V}ar\left[\Vert \boldsymbol{w}\Vert^2\right] = \mathbb{E}\left[\Vert \boldsymbol{w}\Vert^4\right] - \mathbb{E}\left[\Vert \boldsymbol{w}\Vert^2\right]^2 = 2d\sigma^4\end{equation}
这个方差大小也代表着$\Vert \boldsymbol{w}\Vert\approx \sqrt{d}\sigma$的近似程度，也就是说原本的采样方差$\sigma^2$越小，那么近似程度越高。特别地，常见的采样方差是$1/d$（对应$\Vert \boldsymbol{w}\Vert\approx 1$，即单位向量），那么代入上式得到$2/d$，意味着维度越高近似程度越高。此外，如果采样分布不是正态分布，可以另外重新计算$\mathbb{E}\left[w^4\right]$，或者直接将正态分布的结果作为参考结果，反正都只是一个估算罢了。

如果$\boldsymbol{v}=(v_1,v_2,\cdots,v_d)$是另一个独立同分布向量，那么我们可以用同样的方法估计内积，结果是
\begin{equation}\mathbb{E}\left[\boldsymbol{w}\cdot\boldsymbol{v}\right] = \mathbb{E}\left[\sum_i w_i v_i\right] = \sum_i \mathbb{E}\left[w_i\right] \mathbb{E}\left[v_i\right] = 0\label{eq:dot}\end{equation}
以及
\begin{equation}\begin{aligned}\mathbb{E}\left[(\boldsymbol{w}\cdot\boldsymbol{v})^2\right] =&\, \mathbb{E}\left[\left(\sum_i w_i v_i\right)^2\right] = \mathbb{E}\left[\sum_i w_i^2 v_i^2 + \sum_{i,j|i\neq j} w_i v_i w_j v_j\right] \\
=&\, \sum_i \mathbb{E}\left[w_i^2\right]\mathbb{E}\left[w_j^2\right] + \sum_{i,j|i\neq j} \mathbb{E}\left[w_i\right]\mathbb{E}\left[v_i\right]\mathbb{E}\left[w_j\right]\mathbb{E}\left[v_j\right] \\
=&\, d \sigma^4 \\
\end{aligned}\end{equation}
同样地，取$\sigma^2=1/d$的话，那么方差是$1/d^3$，维度越高近似程度越高。以上两个结果可以说是《n维空间下两个随机向量的夹角分布》、《让人惊叹的Johnson-Lindenstrauss引理：理论篇》中的结论的统计版本。

损失分析 #

对语言模型来说，最终要输出一个逐token的$n$元分布，这里$n$是词表大小。假设我们直接输出均匀分布，也就是每个token的概率都是$1/n$，那么不难计算交叉熵损失将会是$\log n$。这也就意味着，合理的初始化不应该使得初始损失明显超过$\log n$，因为$\log n$代表了最朴素的均匀分布，明显超过$\log n$等价于说远远不如均匀分布，就好比是故意犯错，并不合理。

那么，为什么共享Embedding会出现这种情况呢？假设初始Embedding是$\{\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots,\boldsymbol{w}_n\}$，前面已经说了，初始阶段残差分支接近于零，所以输入输入token $i$，模型输出就是经过Normalization之后的Embedding $\boldsymbol{w}_i$。常见的Normalization就是Layer Norm或者RMS Norm，由于初始化分布是零均值的，所以Layer Norm跟RMS Norm大致等价，因此输出是
\begin{equation}\frac{\boldsymbol{w}_i}{\Vert\boldsymbol{w}_i\Vert \big/\sqrt{d}} = \frac{\boldsymbol{w}_i}{\sigma}\end{equation}
接下来重用Embedding，内积然后Softmax，所建立的分布实质是
\begin{equation}p(j|i) = \frac{e^{\boldsymbol{w}_i\cdot \boldsymbol{w}_j / \sigma}}{\sum\limits_k e^{\boldsymbol{w}_i\cdot \boldsymbol{w}_k / \sigma}}\end{equation}
对应的损失函数就是
\begin{equation}-\log p(j|i) = \log \sum\limits_k e^{\boldsymbol{w}_i\cdot \boldsymbol{w}_k / \sigma} - \boldsymbol{w}_i\cdot \boldsymbol{w}_j \big/ \sigma\end{equation}
语言模型任务是为了预测下一个token，而我们知道自然句子中叠词的比例很小，所以基本上可以认为$j\neq i$，那么根据结果$\eqref{eq:dot}$就有$\boldsymbol{w}_i\cdot \boldsymbol{w}_j\approx 0$。所以，初始损失函数是
\begin{equation}-\log p(j|i) \approx \log \sum_k e^{\boldsymbol{w}_i\cdot \boldsymbol{w}_k / \sigma}=\log \left(e^{\boldsymbol{w}_i\cdot \boldsymbol{w}_i / \sigma} + \sum\limits_{k|k\neq i} e^{\boldsymbol{w}_i\cdot \boldsymbol{w}_k / \sigma}\right)\approx\log \left(e^{d \sigma} + (n-1)\right)\label{eq:loss}\end{equation}
后面的$\approx$再次用到了式$\eqref{eq:norm}$和式$\eqref{eq:dot}$。常见的初始化方差$\sigma^2$，或者是一个常数，或者是$1/d$（此时$e^{d \sigma}=e^{\sqrt{d}}$），不管是哪一种，当$d$较大时，都导致$e^{d \sigma}$占主导，于是损失将会是$\log e^{d\sigma}=d\sigma$级别，这很容易就超过了均匀分布的$\log n$。

一些对策 #

根据上述推导结果，我们就可以针对性地设计一些对策了。比较直接的方案是调整初始化，根据式$\eqref{eq:loss}$，我们只需要让$e^{d\sigma}=n$，那么初始损失就是变成$\log n$级别的，也就是说初始化的标准差要改为$\sigma=(\log n)/d$。

一般来说，我们会希望参数的初始化方差尽量大一些，这样梯度相对来说没那么容易下溢，而$\sigma=(\log n)/d$有时候会显得过小了。为此，我们可以换一种思路：很明显，式$\eqref{eq:loss}$之所以会偏大，是因为出现了$e^{\boldsymbol{w}_i\cdot \boldsymbol{w}_i / \sigma}$，由于两个$\boldsymbol{w}_i$相同，它们内积变成了模长，从而变得很大，如果能让它们不同，那么就不会出现这一个占主导的项了。

为此，最简单的方法自然是干脆不共享Embedding，此时是$e^{\boldsymbol{w}_i\cdot \boldsymbol{v}_i / \sigma}$而不是$e^{\boldsymbol{w}_i\cdot \boldsymbol{w}_i / \sigma}$，用$\eqref{eq:dot}$而不是$\eqref{eq:norm}$作为近似，于是式$\eqref{eq:loss}$渐近于$\log n$。如果还想保留共享Embedding，我们可以在最后的Normalization之后，再接一个正交初始化的投影层，这样$e^{\boldsymbol{w}_i\cdot \boldsymbol{w}_i / \sigma}$变成了$e^{(\boldsymbol{w}_i\boldsymbol{P})\cdot \boldsymbol{w}_i / \sigma}$，根据Johnson-Lindenstrauss引理，经过随机投影的向量近似于独立向量了，所以也近似于不共享的情况，这其实就是BERT的解决办法。特别地，这个投影层还可以一般化地加上bias和激活函数。

如果一丁点额外参数都不想引入，那么可以考虑在Normalization之后“打乱”$\boldsymbol{w}_i$的各个维度，比如
\begin{equation}\mathcal{S}[\boldsymbol{w}] = \boldsymbol{w}[d/2:]\circ\boldsymbol{w}[:d/2]\end{equation}
这里的$\circ$是拼接操作，那么$\mathcal{S}[\boldsymbol{w}_i]$和$\boldsymbol{w}_i$也接近正交了，内积自然也约等于0。这相当于（在初始阶段）将原来的$n\times d$的Embedding矩阵劈开为两个$n\times (d/2)$的矩阵然后构建不共享Embedding的2-gram模型。另外，我们还可以考虑其他打乱操作，比如ShuffleNet中的先reshape，然后transpose再reshape回来。

在笔者的实验中，直接改初始化标准差为$\sigma=(\log n)/d$收敛速度是最慢的，其余方法收敛速度差不多，至于最终效果，所有方法似乎都差不多。

文章小结 #

本文重温了语言模型输出端共享Embedding权重的操作，推导了直接重用Embedding来投影输出可能会导致损失过大的可能性，并探讨了一些解决办法。

转载到请包括本文地址：https://kexue.fm/archives/9698

更详细的转载事宜请参考：《科学空间FAQ》