Monarch矩阵：计算高效的稀疏型矩阵分解

在矩阵压缩这个问题上，我们通常有两个策略可以选择，分别是低秩化和稀疏化。低秩化通过寻找矩阵的低秩近似来减少矩阵尺寸，而稀疏化则是通过减少矩阵中的非零元素来降低矩阵的复杂性。如果说SVD是奔着矩阵的低秩近似去的，那么相应地寻找矩阵稀疏近似的算法又是什么呢？

接下来我们要学习的是论文《Monarch: Expressive Structured Matrices for Efficient and Accurate Training》，它为上述问题给出了一个答案——“Monarch矩阵”，这是一簇能够分解为若干置换矩阵与稀疏矩阵乘积的矩阵，同时具备计算高效且表达能力强的特点，论文还讨论了如何求一般矩阵的Monarch近似，以及利用Monarch矩阵参数化LLM来提高LLM速度等内容。

值得指出的是，该论文的作者也正是著名的Flash Attention的作者Tri Dao，其工作几乎都在致力于改进LLM的性能，这篇Monarch也是他主页上特意展示的几篇论文之一，单从这一点看就非常值得学习一番。

SVD回顾 #

首先我们来简单回顾一下SVD（奇异值分解）。对于矩阵$n\times m$大小的矩阵$A$，SVD将它分解为
\begin{equation}A = U\Sigma V\end{equation}
其中$U,V$分别是形状为$n\times n$、$m\times m$的正交矩阵，$\Sigma$则是$n\times m$的对角矩阵，对角线元素非负且从大到小排列。当我们只保留$\Sigma$的前$r$个对角线元素时，就得到了$A$的一个秩不超过$r$的近似分解：
\begin{equation}A \approx U_{[:,:r]}\Sigma_{[:r,:r]} V_{[:r,:]}\end{equation}
这里下标就按照Python的切片来执行，所以$U_{[:,:r]}$的形状为$n\times r$、 $\Sigma_{[:r,:r]}$的形状为$r\times r$以及$V_{[:r,:]}$的形状为$r\times m$，这意味着$U_{[:,:r]}\Sigma_{[:r,:r]} V_{[:r,:]}$的秩至多为$r$。

特别地，由SVD得到的如上低秩近似，正好是如下优化问题的精确解：
\begin{equation}U_{[:,:r]}\Sigma_{[:r,:r]} V_{[:r,:]} = \mathop{\text{argmin}}_{rank(B)\leq r} \Vert A - B\Vert_F^2\end{equation}
其中$\Vert\cdot\Vert_F^2$是矩阵的Frobenius范数的平方，即矩阵每个元素的平方和。也就是说，在Frobenius范数下，矩阵$A$的最优$r$秩近似就是$U_{[:,:r]}\Sigma_{[:r,:r]} V_{[:r,:]}$，该结论被称为“Eckart-Young-Mirsky定理”。也正是因为这个结论，我们在文章开头才说“SVD是奔着矩阵的低秩近似去的”。

SVD可以展开讨论的内容非常多，甚至写成一本书也不为过，这里就不再继续深入了。最后说一下，SVD的计算复杂度是$\mathcal{O}(nm\cdot\min(m,n))$，因为我们至少要对$A^{\top} A$或$A A^{\top}$之一做特征值分解。如果我们确定做SVD是为了寻找$r$秩近似，那么复杂度可以有所降低，这便是Truncated SVD。

Monarch矩阵 #

低秩分解应用非常广，但它未必总是符合我们的需求，比如可逆方阵的低秩近似必然不可逆，这意味着低秩近似不适合需要求逆的场景。此时另一个选择是稀疏近似，稀疏矩阵通常能够保证秩不退化。

注意稀疏和低秩并无必然联系，比如单位阵就是很稀疏的矩阵，但它可逆（满秩）。寻找矩阵的稀疏近似并不难，比如将绝对值最大的$k$个元素外的所有元素都置零就是一个很朴素的稀疏近似，但问题是它通常不实用，所以难在寻找实用的稀疏近似。所谓“实用”，指的是保留足够表达能力或近似程度的同时，实现一定程度的稀疏化，并且这种稀疏化具有适当的结构，有助于矩阵运算（比如乘法、求逆）的提速。

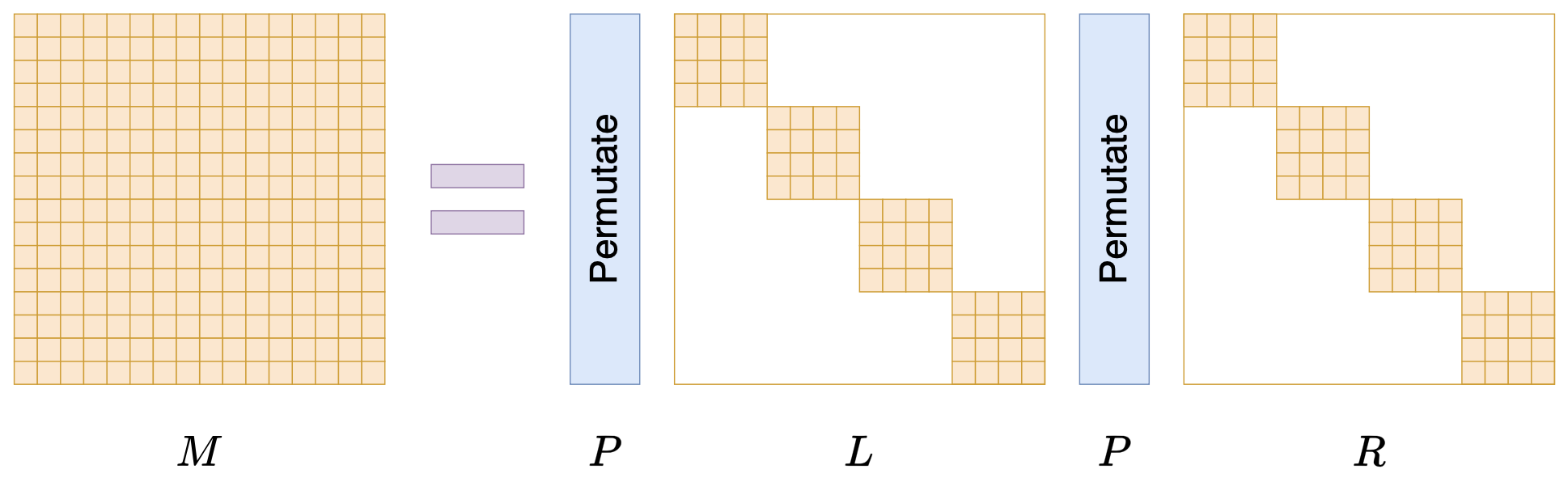
Monarch矩阵正是为此而生，假设$n=m^2$是一个平方数，那么Monarch矩阵是全体$n$阶矩阵的一个子集，我们记为$\mathcal{M}^{(n)}$，它定义为如下形式的矩阵的集合：
\begin{equation}M = PLPR\end{equation}
其中$P$是$n\times n$的置换矩阵（正交矩阵），$L,R$是分块对角矩阵。下面我们来逐一介绍它们。

置换矩阵 #

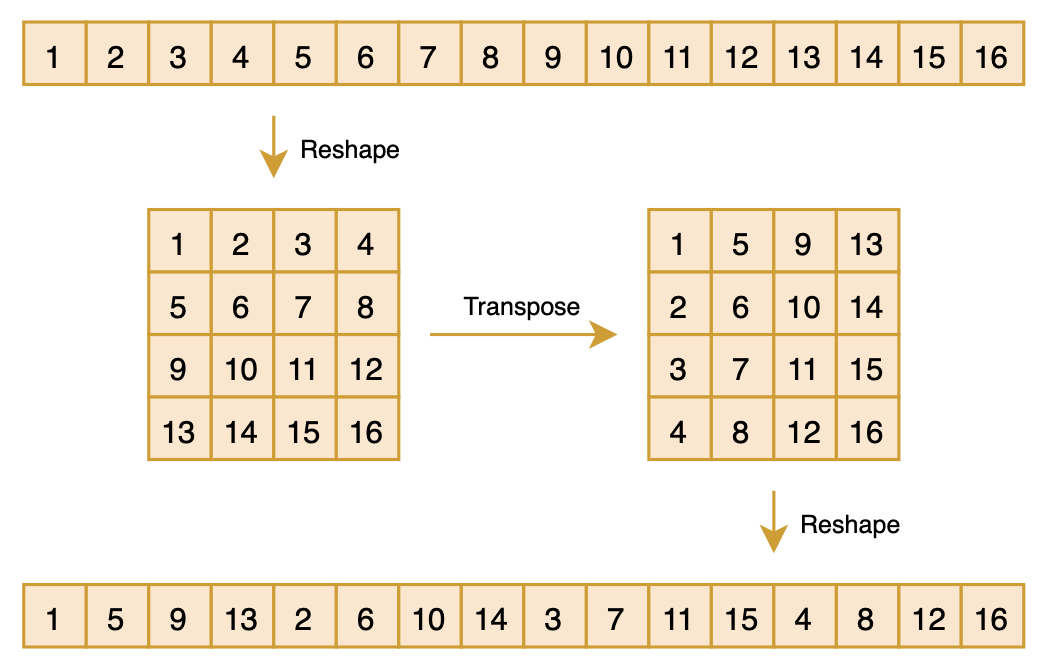
置换矩阵$P$实现的效果是将向量$[x_1,x_2,\cdots,x_n]$置换成新的向量
\begin{equation}[x_1, x_{1+m}, \cdots , x_{1+(m−1)m}, x_2, x_{2+m}, \cdots , x_{2+(m−1)m}, \cdots , x_m, x_{2m}, \cdots , x_n]\end{equation}
当然这样写大家可能依然觉得迷糊，然事实上用代码实现非常简单：

Px = x.reshape(m, m).transpose().reshape(n)

如下图所示：

之前做CV的读者可能会觉得这个操作有点熟悉，它其实就是ShuffleNet中的“Shuffle”操作，这样对向量先reshape然后transpose最后再reshape回来的组合运算，起到一种“伪Shuffle”的效果，它也可以视为$m$进制的“位反转排序”。很明显，这样的操作做两次，所得向量将复原为原始向量，所以我们有$P^2=I$，所以$P^{-1}=P^{\top}=P$。

分块对角 #

说完$P$，我们再来说$L,R$，它们也是$n\times n$大小的矩阵，不过它们还是$m\times m$的分块对角矩阵，每个块是$m\times m$大小，如下图所示：

当$n$足够大时，$L,R$中零的数量占主导，所以$L,R$都是稀疏矩阵，即Monarch矩阵是具备稀疏特性的矩阵分解形式。由于$P$是固定的，所以$PLPR$中的可变元素就来源于$L,R$的非零元素，因此，矩阵$M$虽然是$n\times n$的矩阵，但它实际自由参数不超过$2m^3=2n^{1.5}$个。从$1.5$这个数字我们就可以窥见Monarch矩阵的意图了，它希望将原本需要平方复杂度的运算，通过Monarch矩阵近似降低到1.5次方复杂度。

效率简析 #

那么Monarch矩阵能否达到这个目的呢？换句话说Monarch矩阵能否达到前面说的“实用”标准？表达能力方面我们后面再谈，我们先看计算高效方面。

比如“矩阵-向量”乘法，标准的复杂度是$\mathcal{O}(n^2)$，但如果是Monarch矩阵的话我们有$Mx = P(L(P(Rx)))$，由于乘$P$只是简单的reshape和transpose，所以它几乎不占计算量，主要计算量来源于$L$或$R$跟一个向量相乘。由于$L,R$的分块对角矩阵的特点，我们可以将向量为$m$组，继而转化为$m$个$m\times m$的矩阵与$m$维向量相乘，总复杂度是$2m\times\mathcal{O}(m^2)=\mathcal{O}(2n^{1.5})$，比$\mathcal{O}(n^2)$更低。

再比如求逆，我们考虑$M^{-1}x$，$n$阶矩阵求逆的标准复杂度是$\mathcal{O}(n^3)$，但对于Monarch矩阵我们有$M^{-1} x =R^{-1}PL^{-1}P x$，主要计算量来源于$L^{-1}$、$R^{-1}$以及对应的“矩阵-向量”乘法，由于$L,R$都是分块对角阵，我们只需要分别对每个对角线上的块矩阵求逆，也就是共有$2m$个$m\times m$的矩阵求逆，复杂度是$2m\times\mathcal{O}(m^3)=\mathcal{O}(2n^2)$，同样低于标准的$\mathcal{O}(n^3)$。要单独写出$M^{-1}$也是可以的，但需要利用到后面的恒等式$\eqref{eq:high-m-lr}$。

所以结论就是，由于$P$乘法几乎不占计算量以及$L,R$是分块对角矩阵的特点，$n$阶Monarch矩阵相关运算，基本上可以转化为$2m$个$m\times m$矩阵的独立运算，从而降低总的计算复杂度。所以至少计算高效这一点，Monarch矩阵是没有问题的，并且由于$L,R$的非零元素本身已经方形结构，实现上也很方便，可以充分利用GPU进行计算，不会带来不必要的浪费。

Monarch分解 #

确认Monarch矩阵的有效性后，接下来应用方面的一个关键问题就是：给定任意的$n=m^2$阶矩阵$A$，如何求它的Monarch近似呢？跟SVD类似，我们定义如下优化问题
\begin{equation}\mathop{\text{argmin}}_{M\in\mathcal{M}^{(n)}} \Vert A - M\Vert_F^2\end{equation}
非常幸运的是，这个问题有一个复杂度不超过$\mathcal{O}(n^{2.5})$的求解算法，这比SVD的$\mathcal{O}(n^3)$还要更高效一些。

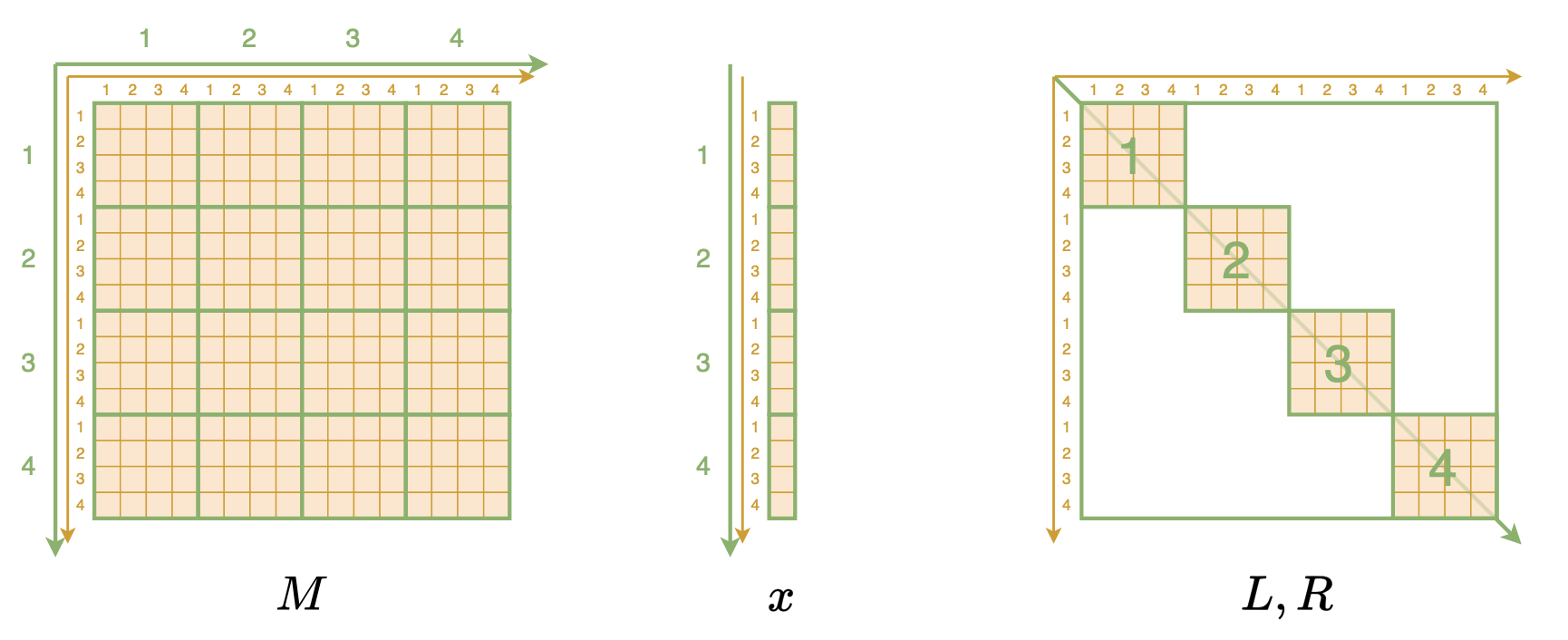
高维数组 #

理解这个算法的关键一步，是将Monarch相关的矩阵、向量都转化为更高维数组的形式。具体来说，Monarch矩阵$M$本来是一个二维数组，每个元素记为$M_{i,j}$，表示该元素位于第$i$行、第$j$列，现在我们要按照分块矩阵的特点，将它等价地表示为四维数组，每个元素记为$M_{i,j,k,l}$，表示第$i$大行、第$j$小行、第$k$大列、第$l$小列的元素，如下图所示：

虽然说起来挺费劲的，但事实上代码就一行

M.reshape(m, m, m, m)

同理，$n$维（列）向量$x$也被转为$m\times m$的二维数据，代码也是一行x.reshape(m, m)。剩下的$L,R$自然是表示为$m\times m\times m$的三维数组，如$L_{i,j,k}$表示第$i$块、第$j$小行、第$k$小列的元素，这本来也是$L,R$最高效的储存方式，但为了统一处理，我们也可以用Kronecker delta符号将它们升到四维，比如$L_{i,j,k,l} = \delta_{i,k}L_{i,j,l}$、$R_{i,j,k,l} = \delta_{i,k}R_{i,j,l}$。

新恒等式 #

接下来，我们将推出$M$与$L,R$的一个新关系式。首先，可以证明在二维表示中，矩阵$P$与向量$x$的乘法变得更简单了，结果就是$x$的转置，即$(Px)_{i,j} = x_{j,i}$，所以我们有$(PR)_{i,j,k,l} = R_{j,i,k,l} = \delta_{j,k}R_{j,i,l}$；接着，两个矩阵的乘法，在四维表示之下求和指标也有两个，所以
\begin{equation}(L P R)_{\alpha,\beta,k,l} = \sum_{i,j} L_{\alpha,\beta,i,j}(PR)_{i,j,k,l} = \sum_{i,j} \delta_{\alpha, i} L_{\alpha,\beta,j}\delta_{j,k}R_{j,i,l} = L_{\alpha,\beta,k}R_{k,\alpha,l}\end{equation}
最后就是$(P L P R)_{\alpha,\beta,k,l}=L_{\beta,\alpha,k}R_{k,\beta,l}$，将$\alpha,\beta$换回$i,j$得到$(P L P R)_{i,j,k,l}=L_{j,i,k}R_{k,j,l}$，又因为$M=PLPR$，所以有
\begin{equation}M_{i,j,k,l} = L_{j,i,k}R_{k,j,l}\label{eq:high-m-lr}\end{equation}
从这个等式可以看出，当我们固定一对$(j,k)$时，左边是一个子矩阵，右边是两个向量的外积，这意味着如果我们要给矩阵$A$找Monarch近似，只需要将$A$按照同样方式转为四维数组，并固定一对$(j,k)$，那么问题就变成了找对应子矩阵的“秩-1近似”！换句话说，有了这个恒等式之后，给矩阵$A$找Monarch近似可以转化为给$m^2$个子矩阵找“秩-1近似”，这可以用SVD完成，每个复杂度不超过$\mathcal{O}(m^3)$，所以总复杂度不超过$m^2\times\mathcal{O}(m^3) = \mathcal{O}(n^{2.5})$。

参考实现 #

笔者简单用Numpy写的参考实现如下：

import numpy as np

def monarch_factorize(A):
    M = A.reshape(m, m, m, m).transpose(1, 2, 0, 3)
    U, S, V = np.linalg.svd(M)
    L = (U[:, :, :, 0] * S[:, :, :1]**0.5).transpose(0, 2, 1)
    R = (V[:, :, 0] * S[..., :1]**0.5).transpose(1, 0, 2)
    return L, R

def convert_3D_to_2D(LR):
    X = np.zeros((m, m, m, m))
    for i in range(m):
        X[i, i] += LR[i]
    return X.transpose(0, 2, 1, 3).reshape(n, n)

m = 8
n = m**2
A = np.where(np.random.rand(n, n) > 0.8, np.random.randn(n, n), 0)

L, R = monarch_factorize(A)
L = convert_3D_to_2D(L)
R = convert_3D_to_2D(R)
PL = L.reshape(m, m, n).transpose(1, 0, 2).reshape(n, n)
PR = R.reshape(m, m, n).transpose(1, 0, 2).reshape(n, n)

U, S, V = np.linalg.svd(A)

print('Monarch error:', np.square(A - PL.dot(PR)).mean())
print('Low-Rank error:', np.square(A - (U[:, :m] * S[:m]).dot(V[:m])).mean())

笔者简单对比了一下SVD求出的秩-$m$近似（此时低秩近似跟Monarch近似参数量相当），发现如果是完全稠密的矩阵，那么秩-$m$近似的平方误差往往优于Monarch近似（但不多），这也是意料之中，因为从Monarch近似的算法就可以看出它本质上也是个定制版的SVD。不过，如果待逼近矩阵是稀疏矩阵时，那么Monarch近似的误差往往更优，并且越稀疏越优。

Monarch推广 #

到目前为止，我们约定所讨论的矩阵都是$n$阶方阵，并且$n=m^2$是一个平方数。如果说方阵这个条件尚能接受，那么$n=m^2$这个条件终究还是太多限制了，因此有必要至少将Monarch矩阵的概念推广到非平方数$n$。

非平方阶 #

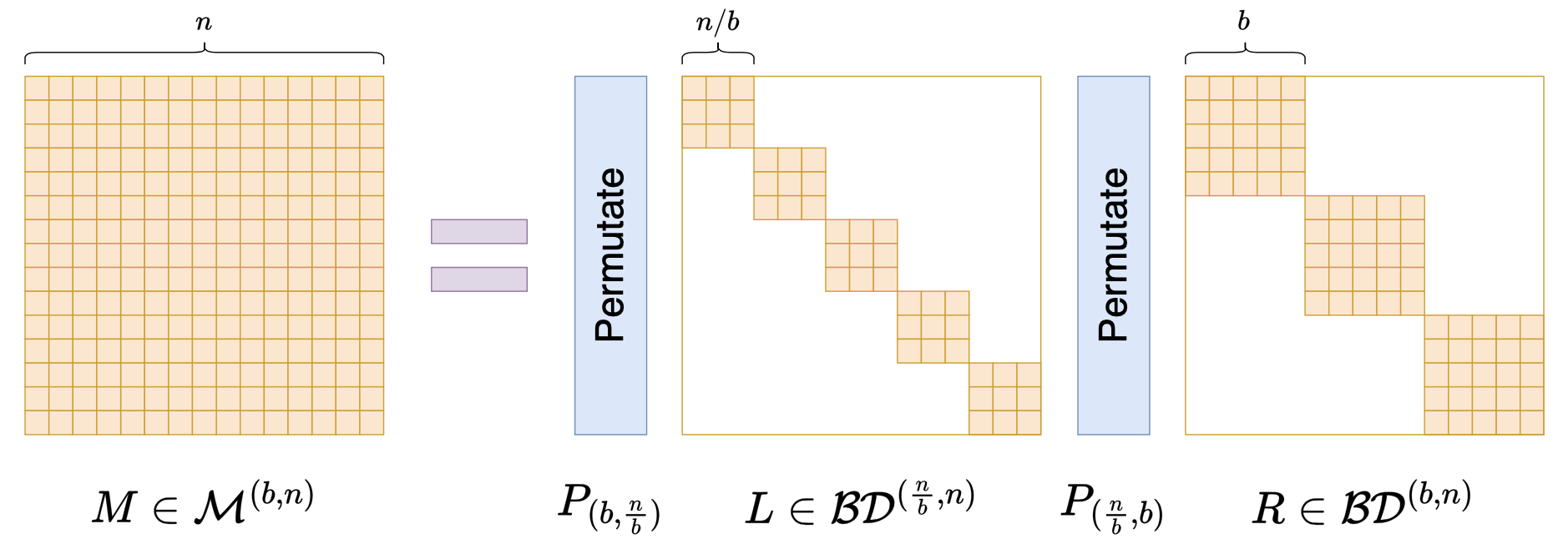
为此，我们先引入一些记号。假设$b$是$n$的一个因数，$\mathcal{BD}^{(b,n)}$表示全体$\frac{n}{b}\times \frac{n}{b}$大小的分块对角矩阵，其中每个块大小是$b\times b$的子矩阵，很明显它是前面$L,R$的一般化，按照这个记号我们可以写出$L,R\in\mathcal{BD}^{(\sqrt{n},n)}$。此外，我们还要一般化置换矩阵$P$，前面我们说了$P$的实现是Px = x.reshape(m, m).transpose().reshape(n)，现在我们一般化为Px = x.reshape(n // b, b).transpose().reshape(n)，记为$P_{(\frac{n}{b},b)}$。

有了这些记号，我们可以定义一般的Monarch矩阵（原论文的附录）：
\begin{equation}\mathcal{M}^{(b,n)} = \Bigg\{M = P_{(b,\frac{n}{b})} L P_{(\frac{n}{b},b)} R\,\Bigg|\, L\in\mathcal{BD}^{(\frac{n}{b},n)}, R\in\mathcal{BD}^{(b,n)} \Bigg\}\end{equation}
示意图如下：

前面所定义的Monarch矩阵，在这里可以简单记为$\mathcal{M}^{(n)} = \mathcal{M}^{(\sqrt{n},n)}$。不难计算，$L$的非零元素至多有$\frac{n^2}{b}$个，$R$的非零元素至多有$nb$个，加起来是$\frac{n^2}{b} + nb$，它在$b=\sqrt{n}$取得最小值，所以$b=\sqrt{n}$属于最稀疏的一个例子。

只要形式 #

可能读者会困惑，为什么要区分$L\in\mathcal{BD}^{(\frac{n}{b},n)}, R\in\mathcal{BD}^{(b,n)}$，统一用一个不行吗？事实上，这样设计是为了保持高维表示下式$\eqref{eq:high-m-lr}$依然成立，从而可以推出类似的分解算法（请读者补充一下），以及可以从理论上保证它的表达能力。

如果我们不在意这些理论细节，只希望构造一个带有稀疏特性的矩阵参数化方式，那么就可以更灵活地对Monarch矩阵进行推广了，比如
\begin{equation}M = \left(\prod_{i=1}^k P_i B_i\right)P_0\end{equation}
其中$B_1,B_2,\cdots,B_k \in \mathcal{BD}^{(b,n)}$，$P_0,P_1,\cdots,P_k$都是置换矩阵，最后多乘一个$P_0$是出于对称性的考虑，并不是必须的，如果你觉得有必要，还可以给每个$B_i$选择不同的$b$，即$B_i\in \mathcal{BD}^{(b_i,n)}$。

甚至，你可以结合低秩分解的形式，推广到非方阵的块矩阵，如下图：

基于这个类比，我们还可以进一步将Monarch矩阵的概念推广到非方阵。总之，如果只是需要一种类似Monarch矩阵的稀疏化结构矩阵，而不在意理论细节，那么结果就仅限于我们的想象力了。

应用例子 #

目前看来，Monarch矩阵最大的特点就是对矩阵乘法比较友好，所以最大的用途无非就是替换全连接层的参数矩阵，从而提高全连接层的效率，这也是原论文实验部份的主要内容。

我们又可以将其分为“事前处理”和“事后处理”两类：“事前处理”就是在训练模型之前就将全连接层的参数矩阵改为Monarch矩阵，这样训练和推理都能提速，训练出来的模型也最贴合Monarch矩阵；“事后处理”就是已经有一个训练好的模型，此时我们可以用Monarch分解给全连接层的参数矩阵找一个Monarch近似，然后替换掉原来的矩阵，必要时再简单微调一下，以此提高原始模型的微调效率或推理效率。

除了替换全连接层外，《Monarch Mixer: A Simple Sub-Quadratic GEMM-Based Architecture》还讨论了更极端的做法——作为一个Token-Mixer模块直接替换Attention层。不过就笔者看来，Monarch-Mixer并不算太优雅，因为它跟MLP-Mixer一样，都是用一个可学的矩阵替换掉Attention矩阵，只不过在Monarch-Mixer这里换成了Monarch矩阵。这样的模式学到的是静态的注意力，个人对其普适性是存疑的。

最后，对如今的LLM来说，Monarch矩阵还可以用来构建参数高效的微调方案（Parameter-Efficient Fine-Tuning，PEFT）。我们知道，LoRA是从低秩分解出发设计的，既然低秩和稀疏是两条平行的路线，那么作为稀疏的代表作Monarch矩阵不应该也可以用来构建一种PEFT方案？Google了一下，还真有这样做的，论文名是《MoRe Fine-Tuning with 10x Fewer Parameters》，还很新鲜，是ICML2024的Workshop之一。

蝶之帝王 #

最后再简单说说Monarch矩阵的拟合能力。“Monarch”意为“帝王”、“君主”，取自“Monarch Butterfly（帝王蝴蝶）”一词，之所以这样命名，是因为它对标的是更早的“Butterfly矩阵”。

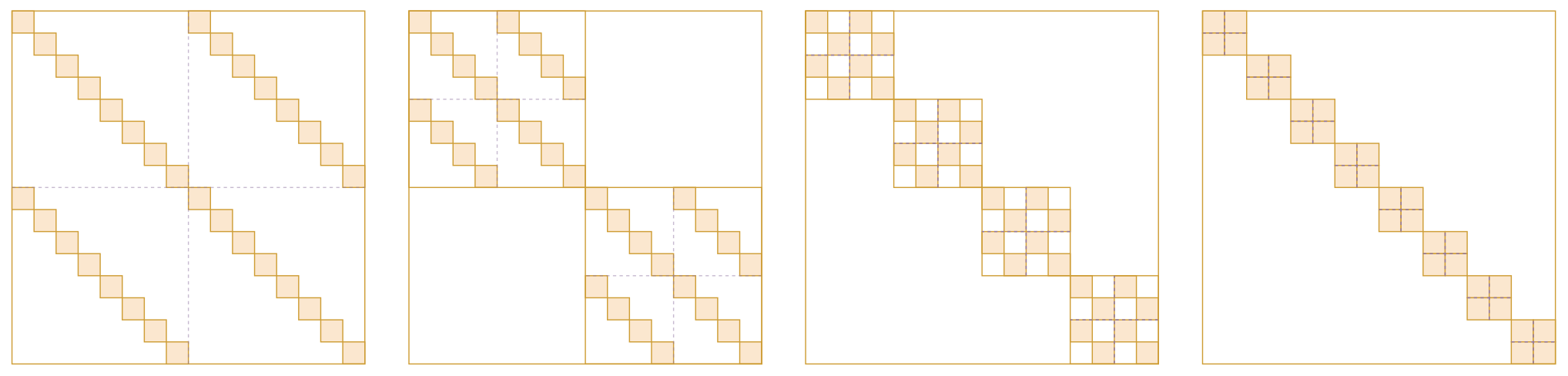
什么是Butterfly矩阵？这个说起来还真有点费劲。Butterfly矩阵是一系列（$\log_2 n$个）Butterfly因子矩阵的乘积，而Butterfly因子矩阵则是一个分块对角矩阵矩阵，其对角线上的矩阵叫做Butterfly因子（没有“矩阵”两个字），Butterfly因子则是一个$2\times 2$的的分块矩阵，它的每个块矩阵则是一个对角阵（套娃结束）。如下图所示：

准确的Butterfly矩阵定义大家自行看论文就好，这里不详细展开。Butterfly这个名字来源于作者觉得每个Butterfly因子的形状像Butterfly（蝴蝶），当然像不像大家见仁见智，反正作者觉得像。从字面上来看，“Monarch Butterfly”比“Butterfly”更高级（毕竟是“帝王”），这暗示着Monarch矩阵比Butterfly矩阵更强。确实如此，Monarch论文附录证明了，不管$b$取什么，$\mathcal{M}^{(b,n)}$都能覆盖所有的$n$阶Butterfly矩阵，并且$n > 512$时$\mathcal{M}^{(b,n)}$严格大于全体$n$阶Butterfly矩阵集合，换言之Butterfly矩阵能做到的Monarch矩阵也能做到，反之未必。

我们也可以从“矩阵-向量”乘法复杂度来直观感知Monarch矩阵表达能力。我们知道，一个$n\times n$矩阵乘以$n$维向量的标准复杂度是$\mathcal{O}(n^2)$，但对于某些结构化矩阵可以更低，比如傅立叶变换可以做到$\mathcal{O}(n\log n)$，Butterfly矩阵也是$\mathcal{O}(n\log n)$，Monarch矩阵则是$\mathcal{O}(n^{1.5})$，所以Monarch矩阵“应该”是不弱于Butterfly矩阵的。当然，Butterfly矩阵也有它的好处，比如它的逆和行列式都比较好算，这对于Flow模型等需要求逆和行列式的场景更为方便。

文章小结 #

本文介绍了Monarch矩阵，这是Tri Dao前两年提出的一簇能够分解为转置矩阵与稀疏矩阵乘积的矩阵，具备计算高效的特点（众所周知，Tri Dao是高性能的代名词），可以用来为全连接层提速、构建参数高效的微调方式等。

转载到请包括本文地址：https://kexue.fm/archives/10249

更详细的转载事宜请参考：《科学空间FAQ》