对齐全量微调!这是我看过最精彩的LoRA改进(二)
By 苏剑林 | 2024-07-29 | 48543位读者 |前两周笔者写了《对齐全量微调!这是我看过最精彩的LoRA(一)》(当时还没有编号“一”),里边介绍了一个名为“LoRA-GA”的LoRA变体,它通过梯度SVD来改进LoRA的初始化,从而实现LoRA与全量微调的对齐。当然,从理论上来讲,这样做也只能尽量对齐第一步更新后的$W_1$,所以当时就有读者提出了“后面的$W_2,W_3,\cdots$不管了吗?”的疑问,当时笔者也没想太深入,就单纯觉得对齐了第一步后,后面的优化也会严格一条较优的轨迹走。
有趣的是,LoRA-GA才出来没多久,arXiv上就新出了《LoRA-Pro: Are Low-Rank Adapters Properly Optimized?》,其所提的LoRA-Pro正好能回答这个问题!LoRA-Pro同样是想着对齐全量微调,但它对齐的是每一步梯度,从而对齐整条优化轨迹,这正好是跟LoRA-GA互补的改进点。
对齐全量 #
本文接着上一篇文章的记号和内容进行讲述,所以这里仅对上一节的内容做一个简单回顾,不再详细重复介绍。LoRA的参数化方式是
\begin{equation}W = (W_0 - A_0 B_0) + AB\end{equation}
其中$W_0 \in \mathbb{R}^{n\times m}$是预训练权重,$A\in\mathbb{R}^{n\times r},B\in\mathbb{R}^{r\times m}$是新引入的训练参数,$A_0,B_0$是它们的初始化值。
上一节我们说到,全量微调很多时候效果都优于LoRA,所以全量微调就是LoRA最应该对齐的方向。为了定量描述这一点,我们分别写出全量微调和LoRA微调在SGD下的优化公式,结果分别是
\begin{equation} W_{t+1} = W_t - \eta G_t\end{equation}
和
\begin{equation}\begin{gathered}
A_{t+1} = A_t - \eta G_{A,t} = A_t - \eta G_t B_t^{\top},\quad B_{t+1} = B_t - \eta G_{B,t} = B_t - \eta A_t^{\top}G_t \\[8pt]
W_{t+1} = W_t - A_t B_t + A_{t+1} B_{t+1} \approx W_t - \eta(A_t A_t^{\top}G_t + G_tB_t^{\top} B_t)
\end{gathered}\end{equation}
其中$\mathcal{L}$是损失函数,$\eta$是学习率,还有$G_t=\frac{\partial \mathcal{L}}{\partial W_t}$、$G_{A,t}=\frac{\partial \mathcal{L}}{\partial A_t}=\frac{\partial \mathcal{L}}{\partial W_t} B_t^{\top}=G_t B_t^{\top}$以及$G_{B,t}=\frac{\partial \mathcal{L}}{\partial B_t}=A_t^{\top}\frac{\partial \mathcal{L}}{\partial W_t} =A_t^{\top}G_t$。
LoRA-GA的想法是,我们至少要让全量微调和LoRA的$W_1$尽可能相近,于是它最小化目标
\begin{equation}\mathop{\text{argmin}}_{A_0,B_0}\left\Vert A_0 A_0^{\top}G_0 + G_0 B_0^{\top} B_0 - G_0\right\Vert_F^2\end{equation}
其最优解可以通过对$G_0$进行SVD求得,这样我们就可以求出最优的$A_0,B_0$作为$A,B$的初始化。
逐步对齐 #
LoRA-Pro的想法更彻底,它希望对齐全量微调和LoRA的每一个$W_t$。可是要怎样才能做到这一点呢?难道每一步都要最小化$\left\Vert A_t A_t^{\top}G_t + G_t B_t^{\top} B_t - G_t\right\Vert_F^2$?这显然是不对的,因为$A_t,B_t$是由优化器根据$A_{t-1},B_{t-1}$和它们的梯度确定的,并不是可自由调节的参数。
看上去已经没有能够让我们修改的地方了?不,LoRA-Pro非常机智地想到:既然“$A_t,B_t$是由优化器根据$A_{t-1},B_{t-1}$和它们的梯度确定的”,后面的$A_{t-1},B_{t-1}$和梯度我们都没法改,那我们还可以改优化器呀!具体来说,我们将$A_t,B_t$的更新规则改为:
\begin{equation}\begin{gathered}
A_{t+1} = A_t - \eta H_{A,t} \\
B_{t+1} = B_t - \eta H_{B,t}
\end{gathered}\end{equation}
其中$H_{A,t},H_{B,t}$待定,但它们的形状跟$A,B$一致。现在可以写出
\begin{equation}W_{t+1} = W_t - A_t B_t + A_{t+1} B_{t+1} \approx W_t - \eta(H_{A,t} B_t + A_t H_{B,t}) \end{equation}
这时候我们就可以调整$H_{A,t},H_{B,t}$,让这个$W_{t+1}$跟SGD的$W_{t+1}$尽可能相近了:
\begin{equation}\mathop{\text{argmin}}_{H_{A,t},H_{B,t}}\left\Vert H_{A,t} B_t + A_t H_{B,t} - G_t\right\Vert_F^2\end{equation}
下面我们来求解这个优化问题。简单起见,在求解过程中我们省略下标$t$,即考虑
\begin{equation}\mathop{\text{argmin}}_{H_A,H_B}\left\Vert H_A B + A H_B - G\right\Vert_F^2\label{eq:loss}\end{equation}
简化目标 #
由于$H_A,H_B$之间没有约束,所以$H_A,H_B$的优化是独立的,因此我们可以采取先优化$H_A$再优化$H_B$的策略(当然反过来也可以)。当我们优化$H_A$时,$H_B$就相当于是常数,为此,我们可以先考虑如下简化的等价命题
\begin{equation}\mathop{\text{argmin}}_H\left\Vert H B - X\right\Vert_F^2\label{eq:h-xb-loss}\end{equation}
其中$H\in\mathbb{R}^{n\times r},B\in\mathbb{R}^{r\times m},X\in\mathbb{R}^{n\times m}$。如果$r=m$且$B$可逆,那么我们直接可以变为解方程组$HB=X$,即$H=XB^{-1}$。当$r < m$时,我们就要诉诸优化手段,注意到$HB-X$关于$H$是线性的,所以这实质就是线性回归的最小二乘问题,它是有解析解的,答案是
\begin{equation}H = XB^{\top}(B B^{\top})^{-1} \label{eq:h-xb}\end{equation}
其中$B^{\top}(B B^{\top})^{-1}$正是矩阵$B$的“伪逆”。不了解这个答案也不要紧,我们现场推一下。首先,记$\mathcal{l}=\left\Vert H B - X\right\Vert_F^2$,直接求$H$的导数得到
\begin{equation}\frac{\partial l}{\partial H} = 2(HB - X)B^{\top} = 2(HBB^{\top} - XB^{\top})\end{equation}
然后让它等于零就可以解出式$\eqref{eq:h-xb}$。可能有些读者不大了解矩阵求导法则,其实根据求导的链式法则,我们就不难想到$\frac{\partial l}{\partial H}$是$2(HB - X)$与$B$以某种方式相乘起来,然后我们约定$\frac{\partial l}{\partial H}$的形状跟$H$一样,即$n\times r$,那么由$2(HB - X)$和$B$相乘来凑出一个$n\times r$的结果,也只有$2(HB - X)B^{\top}$了。
同理,$\left\Vert AH - X\right\Vert_F^2$对$H$的导数就是$2A^{\top}(AH - X)$,由此可以得到
\begin{equation}\mathop{\text{argmin}}_H\left\Vert AH - X\right\Vert_F^2\quad\Rightarrow\quad H = (A^{\top} A)^{-1}A^{\top}X \label{eq:h-ax}\end{equation}
完整结果 #
有了结论$\eqref{eq:h-xb}$和$\eqref{eq:h-ax}$,我们就可以着手求解$\eqref{eq:loss}$了。首先我们固定$H_B$,那么根据式$\eqref{eq:h-xb}$得到
\begin{equation}H_A = (G - A H_B) B^{\top}(B B^{\top})^{-1}\label{eq:h-a-1}\end{equation}
注意式$\eqref{eq:loss}$的目标函数具有一个不变性:
\begin{equation}\left\Vert H_A B + A H_B - G\right\Vert_F^2 = \left\Vert (H_A + AC) B + A (H_B - CB) - G\right\Vert_F^2\end{equation}
其中$C$是任意$r\times r$的矩阵。也就是说,$H_A$的解可以加/减任意具有$AC$形式的矩阵,只需要$H_B$减/加对应的$CB$就行。根据该性质,我们可以将式$\eqref{eq:h-a-1}$的$H_A$简化成
\begin{equation}H_A = G B^{\top}(B B^{\top})^{-1}\end{equation}
代回目标函数得
\begin{equation}\mathop{\text{argmin}}_{H_B}\left\Vert A H_B - G(I - B^{\top}(B B^{\top})^{-1}B)\right\Vert_F^2\end{equation}
根据式$\eqref{eq:h-ax}$得
\begin{equation}H_B = (A^{\top} A)^{-1}A^{\top}G(I - B^{\top}(B B^{\top})^{-1}B)\end{equation}
留意到$G B^{\top},A^{\top}G$正好分别是$A,B$的梯度$G_A,G_B$,以及再次利用前述不变性,我们可以写出完整的解
\begin{equation}\left\{\begin{aligned} H_A =&\, G_A (B B^{\top})^{-1} + AC \\
H_B =&\, (A^{\top} A)^{-1}G_B(I - B^{\top}(B B^{\top})^{-1}B) - CB
\end{aligned}\right.\end{equation}
最优参数 #
至此,我们求解出了$H_A,H_B$的形式,但解不是唯一的,它有一个可以自由选择的参数矩阵$C$。我们可以选择适当的$C$,来使得最终的$H_A,H_B$具备一些我们所期望的特性。
比如,现在$H_A,H_B$是不大对称的,$H_B$多了$-(A^{\top} A)^{-1}G_B B^{\top}(B B^{\top})^{-1}B$这一项,我们可以将它平均分配到$H_A,H_B$中,使得它们更对称一些,这等价于选择$C = -\frac{1}{2}(A^{\top} A)^{-1}G_B B^{\top}(B B^{\top})^{-1}$:
\begin{equation}\left\{\begin{aligned} H_A =&\, \left[I - \frac{1}{2}A(A^{\top}A)^{-1}A^{\top}\right]G_A (B B^{\top})^{-1} \\
H_B =&\, (A^{\top} A)^{-1}G_B\left[I - \frac{1}{2}B^{\top}(B B^{\top})^{-1}B\right]
\end{aligned}\right.\end{equation}
这个$C$也是如下两个优化问题的解:
\begin{align}
&\,\mathop{\text{argmin}}_C \Vert H_A B - A H_B\Vert_F^2 \\
&\,\mathop{\text{argmin}}_C \Vert H_A B - G\Vert_F^2 + \Vert A H_B - G\Vert_F^2 \\
\end{align}
第一个优化目标可以理解为让$A,B$对最终效果的贡献尽可能一样,这跟《配置不同的学习率,LoRA还能再涨一点?》的假设有一定异曲同工之处,第二个优化目标则是让$H_A B$、$A H_B$都尽可能逼近完整的梯度$G$。以$l=\Vert H_A B - A H_B\Vert_F^2$为例,直接求导得
\begin{equation}\frac{\partial l}{\partial C} = 4A^{\top}(H_A B - A H_B)B^{\top}=4A^{\top}\left[G_A (BB^{\top})^{-1}B + 2ACB\right]B^{\top}\end{equation}
令它等于零我们就可以解出同样的$C$,化简过程比较关键的两步是$[I - B^{\top}(B B^{\top})^{-1}B]B^{\top} = 0$以及$A^{\top}G_A = G_B B^{\top}$。
LoRA-Pro选择的$C$略有不同,它是如下目标函数的最优解
\begin{equation}\mathop{\text{argmin}}_C \Vert H_A - G_A\Vert_F^2 + \Vert H_B - G_B\Vert_F^2\end{equation}
这样做的意图也很明显:$H_A,H_B$是用来取代$G_A,G_B$的,如果在能达到相同效果的前提下,相比$G_A,G_B$的改动尽可能小,不失为一个合理的选择。同样求$C$的导数并让其等于零,化简可得
\begin{equation}A^{\top}A C + C B B^{\top} = -A^{\top} G_A (BB^{\top})^{-1}\end{equation}
现在我们得到关于$C$的一个方程,该类型的方程叫做“Sylvester方程”,可以通过外积符号写出$C$的解析解,但没有必要,因为直接数值求解的复杂度比解析解的复杂度要低,所以直接数值求解即可。总的来说,这些$C$的选择方案,都是在让$H_A,H_B$在某种视角下更加对称一些,虽然笔者没有亲自做过对比实验,但笔者认为这些不同的选择之间不会有太明显的区别。
一般讨论 #
我们来捋一捋到目前为止我们所得到的结果。我们的模型还是常规的LoRA,目标则是希望每一步更新都能逼近全量微调的结果。为此,我们假设优化器是SGD,然后对比了同样$W_t$下全量微调和LoRA所得的$W_{t+1}$,发现要实现这个目标,需要把更新过程中$A,B$的梯度$G_A, G_B$换成上面求出的$H_A,H_B$。
接下来就又回到优化分析中老生常谈的问题:前面的分析都是基于SGD优化器的,但实践中我们更常用的是Adam,此时要怎么改呢?如果对Adam优化器重复前面的推导,结果就是$H_A,H_B$中的梯度$G$要换成全量微调下Adam的更新方向$U$。然而,$U$需要用全量微调的梯度$G$按照Adam的更新规则计算而来,而我们的场景是LoRA,无法获得全量微调的梯度,只有$A,B$的梯度$G_A,G_B$。
不过我们也可以考虑一个近似的方案,前述$H_A B + A H_B$的优化目标就是在逼近$G$,所以我们可以用它来作为$G$的近似来执行Adam,这样一来整个流程就可以走通了。于是我们可以写出如下更新规则
\begin{equation}\begin{array}{l}
\begin{array}{l}G_A = \frac{\partial\mathcal{L}}{\partial A_{t-1}},\,\,G_B = \frac{\partial\mathcal{L}}{\partial B_{t-1}}\end{array} \\
\color{green}{\left.\begin{array}{l}H_A = G_A (B B^{\top})^{-1} \\
H_B = (A^{\top} A)^{-1}G_B(I - B^{\top}(B B^{\top})^{-1}B) \\
\tilde{G} = H_A B + A H_B \end{array}\quad\right\} \text{估计梯度}} \\
\color{red}{\left.\begin{array}{l}M_t = \beta_1 M_{t-1} + (1 - \beta_1) \tilde{G} \\
V_t = \beta_2 V_{t-1} + (1 - \beta_2) \tilde{G}^2 \\
\hat{M}_t = \frac{M_t}{1-\beta_1^t},\,\,\hat{V}_t = \frac{V_t}{1-\beta_2^t},\,\,U = \frac{\hat{M}_t}{\sqrt{\hat{V}_t + \epsilon}}\end{array}\quad\right\} \text{Adam更新}} \\
\color{purple}{\left.\begin{array}{l}U_A = UB^{\top},\,\, U_B = A^{\top} U \\
\tilde{H}_A = U_A (B B^{\top})^{-1} + AC \\
\tilde{H}_B = (A^{\top} A)^{-1}U_B(I - B^{\top}(B B^{\top})^{-1}B) - CB
\end{array}\quad\right\} \text{投影到}A,B} \\
\begin{array}{l}A_t = A_{t-1} - \eta \tilde{H}_A \\
B_t = B_{t-1} - \eta \tilde{H}_B \\
\end{array} \\
\end{array}\end{equation}
这也是LoRA-Pro最终所用的更新算法(更准确地说,LoRA-Pro用的是AdamW,结果稍复杂一些,但并无实质不同)。然而,且不说如此改动引入的额外复杂度如何,这个算法最大的问题就是它里边的滑动更新变量$M,V$跟全量微调一样都是满秩的,也就是说它的优化器相比全量微调并不省显存,仅仅是通过低秩分解节省了参数和梯度的部分显存,这相比常规LoRA的显存消耗还是会有明显增加的。
一个比较简单的方案(但笔者没有实验过)就是直接用$H_A,H_B$替代$G_A,G_B$,然后按照常规LoRA的Adam更新规则来计算,这样$M,V$的形状就跟相应的$A,B$一致了,节省的显存达到了最大化。不过此时的Adam理论基础不如LoRA-Pro的Adam,更多的是跟《对齐全量微调!这是我看过最精彩的LoRA(一)》一样,靠“SGD的结论可以平行应用到Adam”的信仰来支撑。
实验结果 #
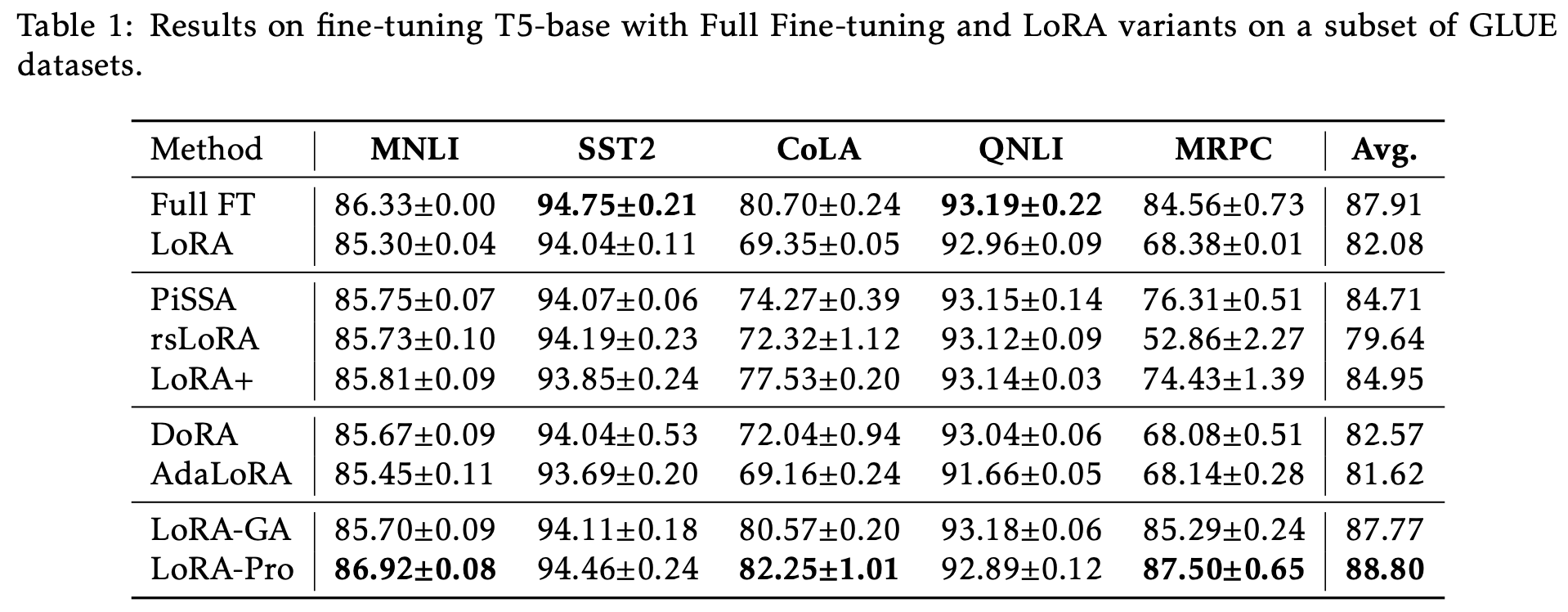
LoRA-Pro在GLUE上的实验结果更加惊艳,超过了全量微调的结果:
不过论文也就只有这个实验了。看上去LoRA-Pro成文比较仓促,可能是看到LoRA-GA后觉得“撞车”感太明显,所以先赶出来占个坑吧。笔者刚刷到LoRA-Pro时,第一反应也是跟LoRA-GA撞车了,但仔细阅读之下才发现,它跟LoRA-GA实际上是同一思想下互补的结果。
从LoRA-Pro的结果来看,它包含了$A^{\top} A$和$B B^{\top}$的求逆,所以很明显$A,B$之一就不能用全零初始化了,比较符合直觉的正交初始化,即让初始的$A^{\top} A,B B^{\top}$是单位阵(的若干倍)。刚好从《对齐全量微调!这是我看过最精彩的LoRA(一)》我们可以看到,LoRA-GA给出的初始化正好是正交初始化,所以LoRA-Pro跟LoRA-GA可谓是“最佳搭档”了。
文章小结 #
本文介绍了另一个对齐全量微调的工作LoRA-Pro,它跟上一篇的LoRA-GA正好是互补的两个结果,LoRA-GA试图通过改进初始化来使得LoRA跟全量微调对齐,LoRA-Pro则更彻底一些,它通过修改优化器的更新规则来使得LoRA的每一步更新都尽量跟全量微调对齐,两者都是非常精彩的LoRA改进,都是让人赏心悦目之作。
转载到请包括本文地址:https://kexue.fm/archives/10266
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jul. 29, 2024). 《对齐全量微调!这是我看过最精彩的LoRA改进(二) 》[Blog post]. Retrieved from https://kexue.fm/archives/10266
@online{kexuefm-10266,
title={对齐全量微调!这是我看过最精彩的LoRA改进(二)},
author={苏剑林},
year={2024},
month={Jul},
url={\url{https://kexue.fm/archives/10266}},
}










August 16th, 2024
复现了一下“最优参数”小节的两种方案,按照“SGD的结论可以平行应用到Adam”的信仰,请苏神看看有没有问题
超参数都按照LoRA-GA论文附录设置,下面三个实验的初始化都使用高斯分布std=1
glue mrpc数据集
LoRA: 83.33%
LoRA pro (19式): 82.11%
LoRA pro (18、24式): 82.84%
glue cola数据集
LoRA: 80.24%
LoRA pro (19式): 78.81%
LoRA pro (18、24式): 78.33%
“信仰”的结果没有超过LoRA,而且在我的实现里需要2倍多训练时间
有意思的是高斯分布std=1初始化下的LoRA结果,和FT的效果就比较接近了
\begin{lstlisting}
# 19式
I_A = torch.eye(A.shape[1]).to(A.device)
I_B = torch.eye(B.shape[0]).to(B.device)
AAT_1 = (A @ A.T).inverse()
BTB_1 = (B.T @ B).inverse()
A.grad = ((I_A - 0.5 * A.T @ AAT_1 @ A) @ A.grad.T @ BTB_1).T
B.grad = (AAT_1 @ B.grad.T @ (I_B - 0.5 * B @ BTB_1 @ B.T)).T
# 18、24式
I_B = torch.eye(B.shape[0]).to(B.device)
AAT = A @ A.T
BTB = B.T @ B
AAT_1 = AAT.inverse()
BTB_1 = BTB.inverse()
X = solve_sylvester(BTB.cpu().detach().numpy(), AAT.cpu().detach().numpy(), (-BTB_1 @ A.grad @ A.T).cpu().detach().numpy())
X = torch.from_numpy(X).to(A.device)
A.grad = BTB_1 @ A.grad + X @ A
B.grad = (I_B - B @ BTB_1 @ B.T) @ B.grad @ AAT_1 - B @ X
\end{lstlisting}
本文的推导只是一个基础结果,据说实际中更多用的是称为stable LoRA的变体,即参数化为$W = (W_0 - s A_0 B_0) + s A B$,这里$s$是个超参数。然后相应的,$A,B$的初始化也可以调整一个scale。我没有调过LoRA,经验不多哈,抱歉。
不过我跟作者交流过,他实验过“信仰”版LoRA-Pro,也说是不大稳定。我给出的建议是使用解析版的$C$,即$(19)$的形式,而不是求解Sylvester方程。
stable lora-ga用起来有点麻烦的,但是效果特别好
(他不能跟pissa一样在推理的时候也进行一波svd分解,所以必须要保存$A_0B_0$)
只搜到了lora-ga,没搜到stable lora-ga,这是什么新技术?
说实话loraga提供的源代码中,超参数设置非常不好,lora的学习率、epoch、初始化的方差随便调一下都能调到比论文里高很多的结果,甚至接近loraga,我是觉得loraga论文里提供的glue实验没什么参考价值
抱歉,这点我倒是没了解到,不过这至少说明LoRA-GA给出了近乎最优的初始化,减少了debug的空间?
嗯嗯是的,我试了一下loraga对超参数比lora稳定的多
研究了一下LoRAPro公开的源代码,首先可以确定作者做的所有实验BA都是零初始化,和苏神提到的"很明显A,B之一就不能用全零初始化了"矛盾,他们目前放出来的代码没有真正调用loraPro算法,实际上只是rslora (目前github上已经有人提了issue和PR)。修复了之后,使用正交初始化或者随机kaiming初始化跑出来,使用pro算法和不使用差距非常小,这里结合苏神的推导感觉Pro的理论算法上应该是没问题的,个人猜测效果不如预期的原因是,我们把求解出来的$H_A,H_B$代回原式,求解出来的$\tilde{g} = H_AB + AH_B\neq g$,他应该仅能让$A^\top\tilde{g}=A^\top g = G_B$和 $\tilde{g}B^\top=g B^\top = G_A$,因为$A,B$都是low rank的,直接让投影变换后的虚拟梯度近似投影后的真实梯度可能并不能很好的对齐,以及我们可以发现他实际上将优化目标等价于用投影后的梯度近似lora梯度 $G_B,G_A$,在实验中我们也发现使用pro算法实际上会把原本出现在lora $G_A,G_B$的变化趋势转移到$H_B,H_A$上,$G_A,G_B$的norm基本上没有什么变化,想请教一下苏神这种理解是否正确
首先,我觉得LoRA-Pro应该要配合LoRA-GA来初始化,因为如果第一步都对不齐的话,后续想对齐也没办法呀~其次,由于LoRA-Pro复杂得多,所以实际表现依赖于哪些细节还真不好说,写这篇博客介绍它也单纯是出于审美上的原因(抱歉,实际上我还没训过LoRA~),所以我的看法可能无法起到什么帮助。
September 6th, 2024
[...]https://kexue.fm/archives/10266[...]
June 16th, 2025
真心实意的向大家请教问题:看了文章“对齐全量微调!这是我看过最精彩的LoRA改进(二)”,我实在想不出来,对于LoRA而言,对齐全参量微调的好处在哪里?我的想法如下:
全参量微调之所以胜过LoRA,其原因在于$\mathcal{\mathcal{\nabla L}}\left(W_{t}\right)$的维度高,是$n\times m$维向量,即要使得$\mathcal{\mathcal{\nabla L}}\left(W_{t}\right)$等于$0$向量是很困难的事情,以致$W_{t}$总可以被更新。但是从公式(5),$$A_{t+1}=A_{t}-\eta H_{A,t}\;B_{t+1}=A_{t}-\eta H_{B,t}$$可知,在梯度下降的方式下权重参数是否更新由$H_{A,t}$和$H_{B,t}$是否为$0$矩阵决定。$H_{A,t}$和$H_{B,t}$的维度,$n\times r$维和$r\times m$维,其维数大大低于$W_{t}$的维数。以致在梯度下降的方式下,即使对齐全参数微调,$H_{A,t}$和$H_{B,t}$依然很容易出现$0$矩阵,实际上公式(18) 可以看出,只要$n \times r$ 维矩阵和$r \times m$维矩阵$$G_{A}=-AC\left(BB^{T}\right)\;G_{B}=\left(A^{T}A\right)CB\left(I-B^{T}\left(BB^{T}\right)^{-1}B\right)$$
时,就会导致$H_{A,t}$和$H_{B,t}$成为$0$矩阵,$A_{t}$和$B_{t}$无法更新,也就是$W_{t}$无法更新,损失函数不再更新。由于我们不能得知$G_{A}$和$G_{B}$的概率分布,所以可以简单的认为$G_{A}=-AC\left(BB^{T}\right)\ $的概率和$G_{A}=0\ $的概率相等,$G_{B}=\left(A^{T}A\right)CB\left(I-B^{T}\left(BB^{T}\right)^{-1}B\right) $的概率和$G_{B}=0\ $的概率相等,即对齐全参数微调和不对其全参数微调的效果一致。因为两种方法在更新变量时遇到极小点的概率一致,所以对于LoRA而言,对齐全参量微调的好处不大。
或许唯一可以解释为什么LoRA对齐全参数微调后效果会有所改善的原因在于:在参数每一次更新,即$W_{t}$变到$W_{t+1}$,$A_{t}$变到$A_{t+1}$,$B_{t}$变到$B_{t+1}$,的过程中,损失函数对参数的梯度$\nabla_{W}\mathcal{L},\nabla_{A}\mathcal{L},\nabla_{B}\mathcal{L}$是在不断变化的。只不过由于$W_{t}$比$A_{t}$和$B_{t}$更靠近神经网络的出口,以致$W_{t}$变到$W_{t+1}$,$A_{t}$变到$A_{t+1}$,$B_{t}$变到$B_{t+1}$,的过程中,$\nabla_{W}\mathcal{L}$的变化比$\nabla_{A}\mathcal{L}$,$\nabla_{B}\mathcal{L}$的变化小一些,以致使用$\nabla_{W_{t}}\mathcal{L}$更能接近参数在这一小段更新过程中的平均梯度。
而且,我认为:没有必要让LoRA中的权重对齐算全参数微调过程中AdamW之后的权重。因为AdamW的做用是让剃度变化大(一会正的梯度很大一会负的剃度很大)的维度上的步长变小,让剃度变化小的(一会正的剃度很小一会负的剃度很小)的维度上的步长变大,从而改变剃度下降法的效果“剃度变化大(一会正的剃度很大一会负的剃度很大)的维度上的步长大,剃度变化小(一会正的剃度很小一会负的剃度很小)的维度上的步长小”。只要提供给AdamW剃度,AdamW就可以很好的改变权重,也就是没有必要让LoRA权重对齐算全参数微调过程中AdamW之后的权重。
这个系列的第一篇文章对齐的思路是改进初始化,第二篇则是尝试对齐每一步增量。我觉得更多是类似主成分的理解吧,假设全量微调总是更佳的前提下,它的低秩投影可以有不同效果,我们尽量挑一个最接近它的版本。
至于你说的容易停止更新(零矩阵)的问题,我觉得并不本质啊,重点不是多快到达极值点(事实上是不是极值点也难说),重点是极值点所对应的train loss和val loss大小。
July 3rd, 2025
老师,您好,向您请教一个问题:会不会因为LoRA中用到的梯度的维度仅仅是全参数微调中梯度的维度的百分之一,导致在LoRA微调的每一次迭代过程中,梯度不能比较准确的反应损失函数与权重参数之间的关系,从而使得反向传播的计算效率低下,进而需要重新设计一个考虑了代表着二阶近似的优化器替代现在使用的AdamW。实际上我准备使用上一时刻损失函数的梯度与当前时刻损失函数的梯度差商计算海瑟矩阵主对角线元素的近似值,利用这个近似值构造二阶近似的优化器。这种想法合理吗?我怕做了这个研究后进行学术论文投稿器时,审稿人认为没有研究价值,被拒搞,恳请大家发表意见
按照我的观点,LoRA这种非常偏应用的场景,没有什么合不合理,只有效果好不好。效果好了,故事不差,那么就可以了。