对齐全量微调！这是我看过最精彩的LoRA改进（一）

众所周知，LoRA是一种常见的参数高效的微调方法，我们在《梯度视角下的LoRA：简介、分析、猜测及推广》做过简单介绍。LoRA利用低秩分解来降低微调参数量，节省微调显存，同时训练好的权重可以合并到原始权重上，推理架构不需要作出改变，是一种训练和推理都比较友好的微调方案。此外，我们在《配置不同的学习率，LoRA还能再涨一点？》还讨论过LoRA的不对称性，指出给$A,B$设置不同的学习率能取得更好的效果，该结论被称为“LoRA+”。

为了进一步提升效果，研究人员还提出了不少其他LoRA变体，如AdaLoRA、rsLoRA、DoRA、PiSSA等，这些改动都有一定道理，但没有特别让人深刻的地方觉。然而，前两天的《LoRA-GA: Low-Rank Adaptation with Gradient Approximation》，却让笔者眼前一亮，仅扫了摘要就有种必然有效的感觉，仔细阅读后更觉得它是至今最精彩的LoRA改进。

究竟怎么个精彩法？LoRA-GA的实际含金量如何？我们一起来学习一下。

基础回顾 #

首先我们再来温习一下LoRA。假设预训练参数为$W_0 \in \mathbb{R}^{n\times m}$，那么全量微调时的更新量自然也是一个$n\times m$矩阵，LoRA将更新量约束为低秩矩阵来降低训练时的参数量，即设$W=W_0 + AB$，其中$A\in\mathbb{R}^{n\times r},B\in\mathbb{R}^{r\times m}$以及$r\ll \min(n,m)$，用新的$W$替换模型原参数，并固定$W_0$不变，只训练$A,B$，如下图所示：
$$\style{display: inline-block; width: 24ex; padding: 10ex 0; border: 1px solid #6C8EBF; background-color: #DAE8FC}{W_0\in\mathbb{R}^{n\times m}} \quad + \quad \style{display: inline-block; width: 8ex; padding: 10ex 0; border: 1px solid #D79B00; background-color: #FFE6CC}{A\in\mathbb{R}^{n\times r}}\quad\times\quad \style{display: inline-block; width: 24ex; padding: 3ex 0; border: 1px solid #D79B00; background-color: #FFE6CC}{B\in\mathbb{R}^{r\times m}}$$

为了使得LoRA的初始状态跟预训练模型一致，我们通常会将$A,B$之一全零初始化，这样可以得到$A_0 B_0=0$，那么初始的$W$就是$W_0$。但这并不是必须的，如果$A,B$都是非全零初始化，那么我们只需要将$W$设置为
\begin{equation}W = (W_0 - A_0 B_0) + AB\end{equation}
也就是说将固定不变的权重从$W_0$换为$W_0 - A_0 B_0$，同样可以满足初始$W$等于$W_0$这一条件。

需要指出的是，LoRA往往只是显存不足的无奈之选，因为一般情况下全量微调的效果都会优于LoRA，所以如果算力足够并且要追求效果最佳时，请优先选择全量微调。这也是LoRA-GA的假设之一，因为它的改进方向就是向全量微调对齐。使用LoRA的另一个场景是有大量的微型定制化需求，我们要存下非常多的微调结果，此时使用LoRA能减少储存成本。

对齐全量 #

LoRA-GA提出了一个非常深刻的优化点：通过$W=(W_0 - A_0 B_0) + AB$我们可以保证$W$的初始值等于$W_0$，即初始状态的LoRA与全量微调是等价的，那么我们是否还可以调整$A_0$和$B_0$，使得LoRA和全量微调在后续训练中也尽可能近似？比如最简单地，让经过第一步优化后的$W_1$尽可能相等？

越仔细回味，我们会越发现这个优化点是如此“直击本质”——LoRA的目标不就是“以小搏大”，希望能接近全量微调的效果吗？既然如此，尽可能对齐全量微调的后续更新结果，不就是最正确的改进方向？从逼近的角度来看，“$W$的初始值等于$W_0$”相当于全量微调的零阶近似，保持后面的$W_1,W_2,\cdots$接近，则相当于是更高阶的近似，是合情合理的选择，所以笔者看完摘要后就有种“就是它了”的强烈感觉。

具体来说，假设我们的优化器是SGD，那么对于全量微调，我们有
\begin{equation} W_1 = W_0 - \eta \frac{\partial \mathcal{L}}{\partial W_0}\end{equation}
其中$\mathcal{L}$是损失函数，$\eta$是学习率。如果是LoRA的话，那么有
\begin{equation}\begin{gathered}
A_1 = A_0 - \eta \frac{\partial \mathcal{L}}{\partial A_0} = A_0 - \eta \frac{\partial \mathcal{L}}{\partial W_0} B_0^{\top},\quad B_1 = B_0 - \eta \frac{\partial \mathcal{L}}{\partial B_0} = B_0 - \eta A_0^{\top}\frac{\partial \mathcal{L}}{\partial W_0} \\[8pt]
W_1 = W_0 - A_0 B_0 + A_1 B_1 \approx W_0 - \eta\left(A_0 A_0^{\top}\frac{\partial \mathcal{L}}{\partial W_0} + \frac{\partial \mathcal{L}}{\partial W_0}B_0^{\top} B_0\right)
\end{gathered}\end{equation}
最后的近似省略了$\eta$的二阶项。现在两个$W_1$具有相似的形式，为了让它们尽可能近似，我们可以考虑最小化
\begin{equation}\mathop{\text{argmin}}_{A_0,B_0}\left\Vert A_0 A_0^{\top}\frac{\partial \mathcal{L}}{\partial W_0} + \frac{\partial \mathcal{L}}{\partial W_0}B_0^{\top} B_0 - \frac{\partial \mathcal{L}}{\partial W_0}\right\Vert_F^2 \label{eq:loss-0}\end{equation}
其中$\Vert\cdot\Vert_F^2$是矩阵的Frobenius范数的平方，即矩阵每个元素的平方和。

求解过程 #

简单起见，我们记$G_0=\frac{\partial \mathcal{L}}{\partial W_0}$，那么目标$\eqref{eq:loss-0}$可以简写成
\begin{equation}\mathop{\text{argmin}}_{A_0,B_0}\left\Vert A_0 A_0^{\top}G_0 + G_0 B_0^{\top} B_0 - G_0\right\Vert_F^2 \label{eq:loss-1}\end{equation}
注意$A_0 A_0^{\top}G_0$、$G_0 B_0^{\top} B_0$的秩顶多为$r$，它们相加后的秩顶多为$2r$，我们假设$2r < \min(n,m)$，所以上述目标相当于寻找$G_0$的一个秩不超过$2r$的最优近似。

我们先考虑$G_0$是非负对角阵的情形，并且对角线元素已经按照从大到小的顺序排列。这个例子很简单，它的秩不超过$2r$的最优近似就是只保留对角线前$2r$个元素的新对角矩阵，这个结论叫做“Eckart-Young-Mirsky定理”，而能让$A_0 A_0^{\top}G_0 + G_0 B_0^{\top} B_0$只保留$G_0$的前$2r$个对角线元素的$A_0,B_0$可以是（分块矩阵）：
\begin{equation}A_0 = (I_n)_{[:, :r]}, \quad B_0 = (I_m)_{[r:2r, :]}\end{equation}
其中$I_n,I_m$分别是$n,m$阶单位阵，${}_{[:, :r]}$和${}_{[r:2r, :]}$就是像Python切片那样，取前$r$列和第$r+1\sim 2r$行。注意我们说的是“可以是”，也就是说解并不唯一，说白了就是要把$G_0$的前$2r$个对角线元素挑出来，$A_0 A_0^{\top}G_0$和 $G_0 B_0^{\top} B_0$各挑一半，至于怎么分配就无所谓了。上面给出的解，对应的是$A_0 A_0^{\top}G_0$挑出前$r$个，$G_0 B_0^{\top} B_0$挑出第$r+1\sim 2r$个。

当$G_0$不是对角阵时，我们将它SVD为$U\Sigma V$，其中$U\in\mathbb{R}^{n\times n},V\in\mathbb{R}^{m\times m}$为正交矩阵，$\Sigma\in\mathbb{R}^{n\times m}$为对角矩阵，对角线元素非负且从大到小排列。代入式$\eqref{eq:loss-1}$后得到
\begin{equation}\begin{aligned}
&\,\left\Vert A_0 A_0^{\top}G_0 + G_0 B_0^{\top} B_0 - G_0\right\Vert_F^2 \\
=&\, \left\Vert A_0 A_0^{\top}U\Sigma V + U\Sigma V B_0^{\top} B_0 - U\Sigma V\right\Vert_F^2 \\
=&\, \left\Vert U\left[(U^{\top}A_0) (U^{\top}A_0)^{\top}\Sigma + \Sigma (B_0 V^{\top})^{\top} (B_0 V^{\top}) - \Sigma \right]V\right\Vert_F^2 \\
=&\, \left\Vert (U^{\top}A_0) (U^{\top}A_0)^{\top}\Sigma + \Sigma (B_0 V^{\top})^{\top} (B_0 V^{\top}) - \Sigma\right\Vert_F^2 \\
\end{aligned}\end{equation}
前两个等号都是简单的代换，第三个等号是因为正交变换不改变Frobenius范数（请读者自行证明一下）。经过这样的转换，我们发现逼近的对象重新转变为对角阵$\Sigma$，自变量则变成了$U^{\top}A_0$、$B_0 V^{\top}$，那么按照$G_0$是对角矩阵时所给出的解，我们得到
\begin{equation}A_0 = U(I_n)_{[:, :r]} = U_{[:, :r]},\quad B_0 = (I_m)_{[r:2r, :]} V = V_{[r:2r, :]}\end{equation}

一般结果 #

现在我们就得到了LoRA的一种初始化方法：

LoRA-GA 选取一批样本，计算初始梯度$G_0 = \nabla_{W_0}\mathcal{L}$，对梯度SVD为$G_0 = U\Sigma V$，取$U$的前$r$列初始化$A$，取$V$的第$r+1\sim 2r$行初始化$B$。

这样LoRA + SGD得到的$W_1$就跟全量微调的$W_1$尽可能相近了。此外，梯度最重要的是方向，其模长不大重要，所以初始化结果我们还可以乘以个scale，LoRA本身也可以乘以个scale，即$W = (W_0 - \lambda A_0 B_0) + \lambda AB$，这些都是LoRA常见的超参数，这里就不展开讨论了。顺便提一下，形式上跟LoRA-GA比较相似的是PiSSA，它是对$W_0$做SVD来初始化$A,B$，这在理论支持上就不如LoRA-GA了，是一个纯粹的经验选择。

当然，可能有读者会发现目前的推导都是基于SGD优化器的假设，那么对于我们更常用的Adam优化器，结论是否要做出改变呢？理论上是要的。我们在《配置不同的学习率，LoRA还能再涨一点？》讨论过，对于Adam来说，第一步优化结果是$W_1 = W_0 - \eta\, \text{sign}(G_0)$而不是$W_1 = W_0 - \eta G_0$，这样重复前面的推导，我们可以得到优化目标为
\begin{equation}\mathop{\text{argmin}}_{A_0,B_0}\left\Vert A_0 \text{sign}(A_0^{\top}G_0) + \text{sign}(G_0 B_0^{\top}) B_0 - \text{sign}(G_0)\right\Vert_F^2 \label{eq:loss-adam}\end{equation}
由于符号函数$\text{sign}$的存在，我们没法求出它的解析解，所以针对Adam的理论分析就只能止步于此了。

在这个背景下，对于Adam优化器，我们有三个选择：

1、信仰：直接引用SGD的结果，相信它也可以在Adam中发挥同样的效果；

2、硬刚：用优化器直接去最小化目标$\eqref{eq:loss-adam}$，由于目标比较简单，计算量尚能接受；

3、投机：直觉上将$G_0$换成$\text{sign}(G_0)$，然后代入SGD的结论，可能更贴合Adam。

看起来原论文选择的是第1个方案，论文的实验结果确实也支持这一选择。

实验效果 #

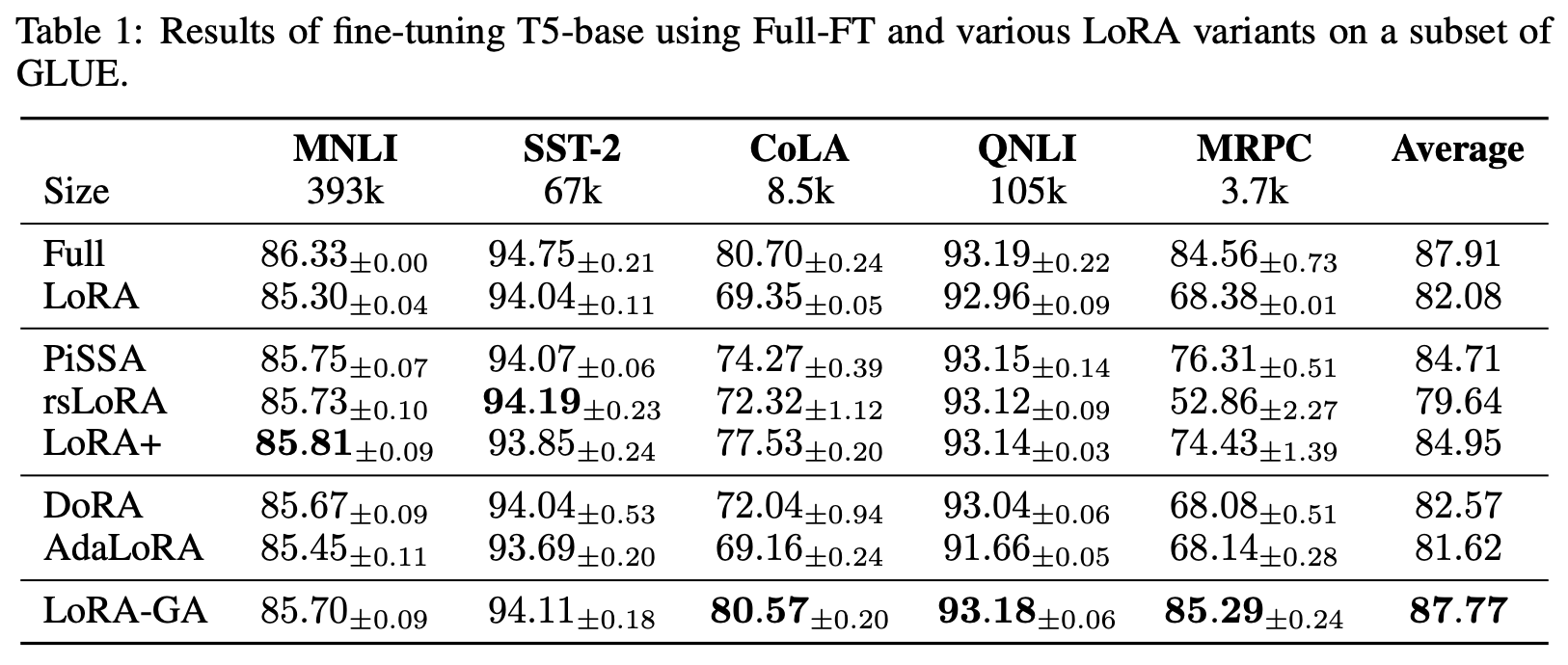
论文的实验结果还是比较惊艳的，尤其是在GLUE上取得了最接近全量微调的效果：

平均来说，训练数据量越少，相对提升的幅度越大，这表明LoRA-GA对齐全量微调的策略，不仅有助于提高最终效果，还能提高训练效率，即可以用更少的训练步数就能达到更优的效果。

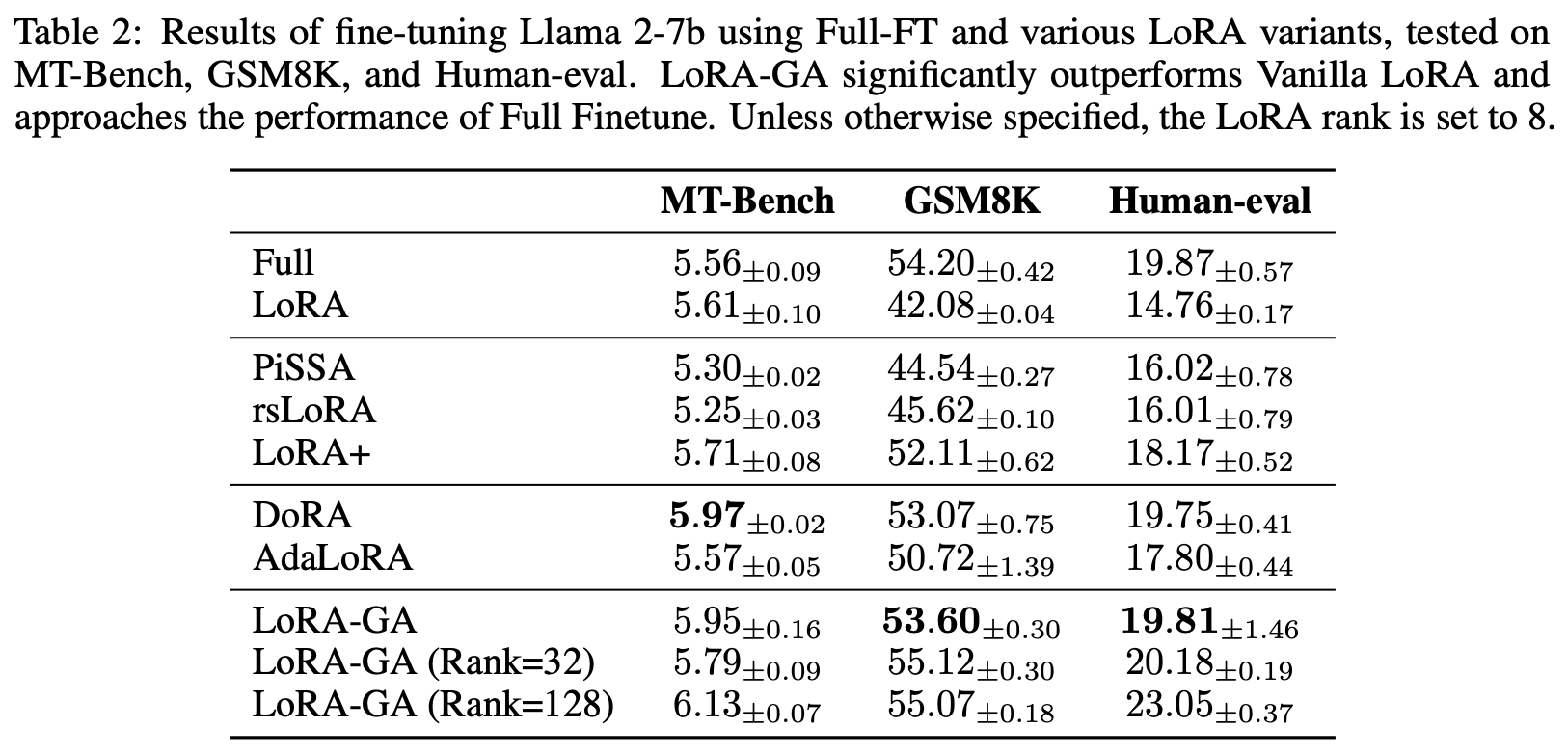
在LLAMA2-7b上的表现也可圈可点：

注意使用LoRA的主要场景是显存不足，但LoRA的初始化需要求出所有训练参数的完整梯度，这可能会由于显存不足而无法实现。为此，原论文提出的技巧是我们可以一个个参数串行地求梯度，而不是同时求所有训练参数的梯度，这样就可以把单步计算的显存降下来。串行求梯度虽然会降低效率，但初始化本身是一次性工作，因此稍慢点也无妨。至于怎么实现这个操作，不同框架有不同方法，这里也不展开讨论了。

文章小结 #

本文介绍了LoRA的一个新改进LoRA-GA。虽然LoRA的各种变体并不鲜见，但LoRA-GA以非常直观的理论指导折服了笔者，其改进思路给人一种“确认过眼神，它就是对的论文”的感觉，再配上可圈可点的实验结果，整个过程如行云流水，让人赏心悦目。

转载到请包括本文地址：https://kexue.fm/archives/10226

更详细的转载事宜请参考：《科学空间FAQ》