生成扩散模型漫谈(十四):构建ODE的一般步骤(上)
By 苏剑林 | 2022-12-15 | 63663位读者 | 引用书接上文,在《生成扩散模型漫谈(十三):从万有引力到扩散模型》中,我们介绍了一个由万有引力启发的、几何意义非常清晰的ODE式生成扩散模型。有的读者看了之后就疑问:似乎“万有引力”并不是唯一的选择,其他形式的力是否可以由同样的物理绘景构建扩散模型?另一方面,该模型在物理上确实很直观,但还欠缺从数学上证明最后确实能学习到数据分布。
本文就尝试从数学角度比较精确地回答“什么样的力场适合构建ODE式生成扩散模型”这个问题。
基础结论
要回答这个问题,需要用到在《生成扩散模型漫谈(十二):“硬刚”扩散ODE》中我们推导过的一个关于常微分方程对应的分布变化的结论。
考虑$\boldsymbol{x}_t\in\mathbb{R}^d, t\in[0,T]$的一阶(常)微分方程(组)
\begin{equation}\frac{d\boldsymbol{x}_t}{dt}=\boldsymbol{f}_t(\boldsymbol{x}_t)\label{eq:ode}\end{equation}
Transformer升级之路:6、旋转位置编码的完备性分析
By 苏剑林 | 2022-12-28 | 44015位读者 | 引用在去年的文章《Transformer升级之路:2、博采众长的旋转式位置编码》中,笔者提出了旋转位置编码(RoPE),当时的出发点只是觉得用绝对位置来实现相对位置是一件“很好玩的事情”,并没料到其实际效果还相当不错,并为大家所接受,不得不说这真是一个意外之喜。后来,在《Transformer升级之路:4、二维位置的旋转式位置编码》中,笔者讨论了二维形式的RoPE,并研究了用矩阵指数表示的RoPE的一般解。
既然有了一般解,那么自然就会引出一个问题:我们常用的RoPE,只是一个以二维旋转矩阵为基本单元的分块对角矩阵,如果换成一般解,理论上效果会不会更好呢?本文就来回答这个问题。
指数通解
在《Transformer升级之路:4、二维位置的旋转式位置编码》中,我们将RoPE抽象地定义为任意满足下式的方阵
\begin{equation}\boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n=\boldsymbol{\mathcal{R}}_{n-m}\label{eq:re}\end{equation}
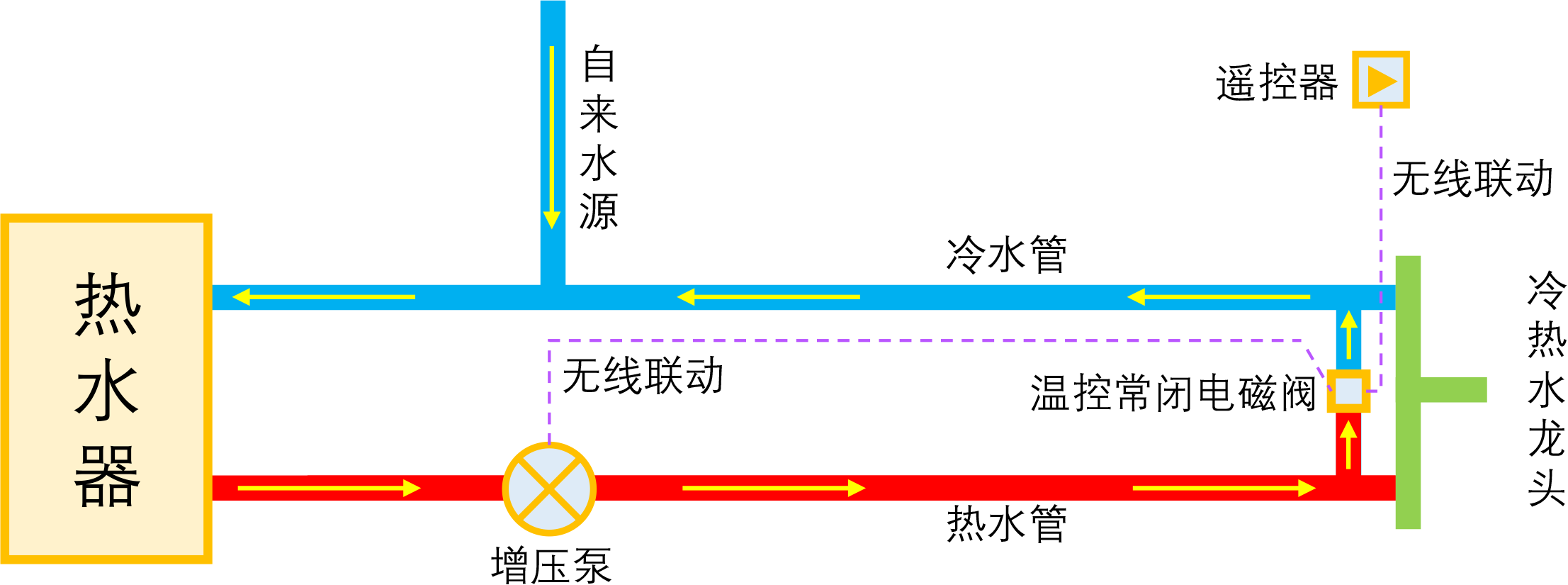
智能家居之热水器零冷水技术原理浅析
By 苏剑林 | 2023-01-04 | 51668位读者 | 引用如果家庭使用单一的热水器集中供热水,那么当我们想要用热水时,往往需要先放一段时间的冷水,而如果放冷水时间比较长的话,就会比较影响体验。所谓零冷水,实际上就是想办法提前把热水管中的冷水排放掉,以达到(几乎)瞬间出热水的效果。事实上,零冷水并不是什么高大上的技术,但可能由于观念没跟上、理解上有误等原因,零冷水技术还没有在家庭中得到普及,不过随着大家对生活品质的要求越来越高,零冷水确实在慢慢流行起来了。
本文来简单分析一下零冷水技术的实现原理,包括各种方案的优缺点和自省DIY的参考思路。
写在前面
在文章开始,需要纠正很多人的一个错误观念:零冷水不是为了省钱,而是为了提升生活品质。如果你是省钱最大的心态,那么接下来的内容就可以不用看了,零冷水技术对你毫无价值。
生成扩散模型漫谈(十六):W距离 ≤ 得分匹配
By 苏剑林 | 2023-02-14 | 26328位读者 | 引用Wasserstein距离(下面简称“W距离”),是基于最优传输思想来度量两个概率分布差异程度的距离函数,笔者之前在《从Wasserstein距离、对偶理论到WGAN》等博文中也做过介绍。对于很多读者来说,第一次听说W距离,是因为2017年出世的WGAN,它开创了从最优传输视角来理解GAN的新分支,也提高了最优传输理论在机器学习中的地位。很长一段时间以来,GAN都是生成模型领域的“主力军”,直到最近这两年扩散模型异军突起,GAN的风头才有所下降,但其本身仍不失为一个强大的生成模型。
从形式上来看,扩散模型和GAN差异很明显,所以其研究一直都相对独立。不过,去年底的一篇论文《Score-based Generative Modeling Secretly Minimizes the Wasserstein Distance》打破了这个隔阂:它证明了扩散模型的得分匹配损失可以写成W距离的上界形式。这意味着在某种程度上,最小化扩散模型的损失函数,实则跟WGAN一样,都是在最小化两个分布的W距离。
Google新搜出的优化器Lion:效率与效果兼得的“训练狮”
By 苏剑林 | 2023-02-16 | 55798位读者 | 引用昨天在Arixv上发现了Google新发的一篇论文《Symbolic Discovery of Optimization Algorithms》,主要是讲自动搜索优化器的,咋看上去没啥意思,因为类似的工作也有不少,大多数结果都索然无味。然而,细读之下才发现别有洞天,原来作者们通过数千TPU小时的算力搜索并结合人工干预,得到了一个速度更快、显存更省的优化器Lion(EvoLved Sign Momentum,不得不吐槽这名字起得真勉强),并在图像分类、图文匹配、扩散模型、语言模型预训练和微调等诸多任务上做了充分的实验,多数任务都显示Lion比目前主流的AdamW等优化器有着更好的效果。
更省显存还更好效果,真可谓是鱼与熊掌都兼得了,什么样的优化器能有这么强悍的性能?本文一起来欣赏一下论文的成果。
先说结果
本文主要关心搜索出来的优化器本身,所以关于搜索过程的细节就不讨论了,对此有兴趣读者自行看原论文就好。Lion优化器的更新过程为
\begin{equation}\text{Lion}:=\left\{\begin{aligned}
&\boldsymbol{u}_t = \text{sign}\big(\beta_1 \boldsymbol{m}_{t-1} + \left(1 - \beta_1\right) \boldsymbol{g}_t\big) \\
&\boldsymbol{\theta}_t = \boldsymbol{\theta}_{t-1} - \eta_t (\boldsymbol{u}_t \color{skyblue}{ + \lambda_t \boldsymbol{\theta}_{t-1}}) \\
&\boldsymbol{m}_t = \beta_2 \boldsymbol{m}_{t-1} + \left(1 - \beta_2\right) \boldsymbol{g}_t
\end{aligned}\right.\end{equation}
Naive Bayes is all you need ?
By 苏剑林 | 2023-06-08 | 52508位读者 | 引用很抱歉,起了这么个具有标题党特征的题目。在写完《NBCE:使用朴素贝叶斯扩展LLM的Context处理长度》之后,笔者就觉得朴素贝叶斯(Naive Bayes)跟Attention机制有很多相同的特征,后来再推导了一下发现,Attention机制其实可以看成是一种广义的、参数化的朴素贝叶斯。既然如此,“Attention is All You Need”不也就意味着“Naive Bayes is all you need”了?这就是本文标题的缘由。
接下来笔者将介绍自己的思考过程,分析如何从朴素贝叶斯角度来理解Attention机制。
朴素贝叶斯
本文主要考虑语言模型,它要建模的是$p(x_t|x_1,\cdots,x_{t-1})$。根据贝叶斯公式,我们有
\begin{equation}p(x_t|x_1,\cdots,x_{t-1}) = \frac{p(x_1,\cdots,x_{t-1}|x_t)p(x_t)}{p(x_1,\cdots,x_{t-1})}\propto p(x_1,\cdots,x_{t-1}|x_t)p(x_t)\end{equation}
关于NBCE方法的一些补充说明和分析
By 苏剑林 | 2023-05-31 | 29003位读者 | 引用上周在《NBCE:使用朴素贝叶斯扩展LLM的Context处理长度》中,我们介绍了一种基于朴素贝叶斯来扩展LLM的Context长度的方案NBCE(Naive Bayes-based Context Extension)。由于它有着即插即用、模型无关、不用微调等优点,也获得了一些读者的认可,总的来说目前大家反馈的测试效果还算可以。
当然,部分读者在使用的时候也提出了一些问题。本文就结合读者的疑问和笔者的后续思考,对NBCE方法做一些补充说明和分析。
方法回顾
假设$T$为要生成的token序列,$S_1,S_2,\cdots,S_n$是给定的若干个Context,我们需要根据$S_1,S_2,\cdots,S_n$生成$T$,那么就需要估计$p(T|S_1, S_2,\cdots,S_n)$。根据朴素贝叶斯思想,我们得到
\begin{equation}\log p(T|S_1, S_2,\cdots,S_n) = \color{red}{(\beta + 1)\overline{\log p(T|S)}} - \color{green}{\beta\log p(T)} + \color{skyblue}{\text{常数}}\label{eq:nbce-2}\end{equation}
Tiger:一个“抠”到极致的优化器
By 苏剑林 | 2023-03-07 | 49564位读者 | 引用这段时间笔者一直在实验《Google新搜出的优化器Lion:效率与效果兼得的“训练狮”》所介绍的Lion优化器。之所以对Lion饶有兴致,是因为它跟笔者之前的关于理想优化器的一些想法不谋而合,但当时笔者没有调出好的效果,而Lion则做好了。
相比标准的Lion,笔者更感兴趣的是它在$\beta_1=\beta_2$时的特殊例子,这里称之为“Tiger”。Tiger只用到了动量来构建更新量,根据《隐藏在动量中的梯度累积:少更新几步,效果反而更好?》的结论,此时我们不新增一组参数来“无感”地实现梯度累积!这也意味着在我们有梯度累积需求时,Tiger已经达到了显存占用的最优解,这也是“Tiger”这个名字的来源(Tight-fisted Optimizer,抠门的优化器,不舍得多花一点显存)。
此外,Tiger还加入了我们的一些超参数调节经验,以及提出了一个防止模型出现NaN(尤其是混合精度训练下)的简单策略。我们的初步实验显示,Tiger的这些改动,能够更加友好地完成模型(尤其是大模型)的训练。








最近评论