生成扩散模型漫谈(十三):从万有引力到扩散模型
By 苏剑林 | 2022-10-18 | 94295位读者 |对于很多读者来说,生成扩散模型可能是他们遇到的第一个能够将如此多的数学工具用到深度学习上的模型。在这个系列文章中,我们已经展示了扩散模型与数学分析、概率统计、常微分方程、随机微分方程乃至偏微分方程等内容的深刻联系,可以说,即便是做数学物理方程的纯理论研究的同学,大概率也可以在扩散模型中找到自己的用武之地。
在这篇文章中,我们再介绍一个同样与数学物理有深刻联系的扩散模型——由“万有引力定律”启发的ODE式扩散模型,出自论文《Poisson Flow Generative Models》(简称PFGM),它给出了一个构建ODE式扩散模型的全新视角。
万有引力 #
中学时期我们就学过万有引力定律,大概的描述方式是:
两个质点彼此之间相互吸引的作用力,是与它们的质量乘积成正比,并与它们之间的距离成平方反比。
这里我们忽略质量和常数,主要关心它的方向和与距离的关系,假设引力源位于$\boldsymbol{y}$,那么位于$\boldsymbol{x}$的物体所受到的引力可以记为
\begin{equation}\boldsymbol{F}(\boldsymbol{x}) = -\frac{1}{4\pi}\frac{\boldsymbol{x} - \boldsymbol{y}}{\Vert \boldsymbol{x} - \boldsymbol{y}\Vert^3}\label{eq:grad-3}\end{equation}
$\frac{1}{4\pi}$这个因子我们可以先不管它,它不影响后面的分析。准确来说,上式描述的是三维空间的引力场,对于$d$维空间来说,其引力场的形式为
\begin{equation}\boldsymbol{F}(\boldsymbol{x}) = -\frac{1}{S_d(1)}\frac{\boldsymbol{x} - \boldsymbol{y}}{\Vert \boldsymbol{x} - \boldsymbol{y}\Vert^d}\label{eq:grad-d}\end{equation}
其中$S_d(1)$是$d$维单位超球面的表面积。该式实际上就是$d$维Poisson方程的格林函数的梯度,这也就是论文标题中的“Poisson”一词的来源。
沿场线走 #
如果引力源有多个,那么直接将各个引力源的引力相加即可,这是引力场的线性可加性。下面我们画出了四个引力源的向量场,其中引力源用黑色点标记出,彩色线表示场线:
从上述引力场图我们可以看出它的一个重要特点:
除了极少数外,大部分场线都是从远处出发,终止于某个引力源点。
此时,一个直观而又“异想天开”的主意是:
如果每个引力源都代表着一个要生成的真实样本点,那么远处的任意点只要沿着场线运动,不就都可以演变成一个真实样本点了吗?
这就是《Poisson Flow Generative Models》一文最核心的天才想法!
等效质心 #
当然,天才归天才,要将它真正变成一个可用的模型,还有很多细节要补充。比如我们刚才说“远处的任意点”,这就是扩散模型的初始分布了,那么问题就来了:“远处”是多远?“任意点”该如何采样?如果采样方式过于复杂,那也没有价值了。
幸运的是,引力场有一个非常重要的等效性质:
无穷远处的多源引力场,等价于位于质心、质量叠加的质点引力场。
也就是说,当距离足够远时,我们只需要当它是位于质心的单源质点引力场。下图也画出了多源引力场及其对应的质心引力场,可以看到,当距离变大时(橙色圆圈位置),两者的引力场几乎一致了。
单个质点的引力场有什么特点?各向同性!这意味着在足够大半径时,可以认为场线是均匀地穿过以质点为球心的球面的,所以我们在一个半径足够大的球面上进行均匀采样就可以了,这就解决了初始分布的采样问题。至于“足够大”是多大,我们后面再说。
模式坍缩 #
所以生成模型就这样构建好了?还没有。引力场的各向同性使得对应的初始分布易于采样,然而也会造成引力源的相互抵消现象,从而出现“模式坍缩(Mode Collapse)”。
具体来说,我们先来画出均匀分布在球壳上的引力场,它的分布是这样的:
发现特点了没?在球壳外部是正常的各向同性分布,但是在球壳内部是“空”的!也就是说球壳内部的引力场相互抵消了,相当于一个真空地带,这个现象笔者在十多年前的科普博客《球壳内部的均匀力场》也介绍过。
抵消现象意味着任意选一个球面,球面上均匀分布的引力源由于引力相互抵消,那么就相当于不存在该引力源了。而我们说了,本文构建生成模型的方式,是通过远处的任意点沿着场线运动,直达某个引力源。如果引力源相互抵消,那么就意味着永远也达不到某些引力源,即意味着某些真实样本无法生成,生成结果就会缺失多样性,这就是“模式坍缩”现象。
增加一维 #
看上去模式坍缩无论如何都是不能避免的。因为在构建生成模型的时候,我们通常假设真实样本服从一个连续型的分布,这样一来,任选一个球面,哪怕真实样本在该球面的分布不是均匀的,我们也能从中挑出一个均匀分布的“子集”,该“子集”的引力就相互抵消了,相当于这些数据点不存在了,继而发生模式坍缩。
那么这条路真的走到尽头了吗?并没有!这时候PFGM的第二个“天才想法”来了:增加一维!
刚才我们分析了,模式坍缩无法避免,是因为连续性分布的假设导致各向同性无法避免。要想避免模式坍缩,就要想办法杜绝分布的各向同性。可是真实样本的分布是目标分布,这是不能改变的,然而我们可以给它增加一维,如果我们在$d+1$维空间去讨论,那么原来的$d$维分布可以视为$d+1$维空间的一个平面,平面就不可能各向同性了。举个低维空间的例子。我们知道对于二维空间来说,“圆”是各向同性的,但对于三维空间来说,“球”才是各向同性的,二维空间中各向同性的“圆”,在三维空间看来就不是各向同性了。
所以,假设要生成的真实样本原来是$\boldsymbol{x}\in\mathbb{R}^d$的,我们引入一个新维度$t$,使得数据点变为$(\boldsymbol{x},t)\in\mathbb{R}^{d+1}$,而原来真实样本服从的分布是$\boldsymbol{x}\sim \tilde{p}(\boldsymbol{x})$的,现在改为$(\boldsymbol{x},t)\sim \delta(t)\tilde{p}(\boldsymbol{x})$,其中$\delta(t)$是狄拉克分布,其实就是将真实样本放到$d+1$维空间的$t=0$平面上。这样处理后,在$d+1$维空间中,真实样本点的$t$取值总是0,因此就不能出现各向同性现象了(类比刚才“三维空间中的圆”的例子)。
豁然开朗 #
乍一看,增加一维只是一个数学上的小技巧,但细细品味之下,我们会越发感觉它妙不可言,很多在原来$d$维空间中不好处理的细节问题,在$d+1$维空间中就豁然开朗了。
根据式$\eqref{eq:grad-d}$和引力的线性叠加性,我们可以写出此时$d+1$维空间的引力场为
\begin{equation}\begin{aligned}
\boldsymbol{F}(\boldsymbol{x}, t) =&\, -\frac{1}{S_{d+1}(1)}\iint\frac{(\boldsymbol{x} - \boldsymbol{x}_0, t - t_0)}{(\Vert\boldsymbol{x} - \boldsymbol{x}_0\Vert^2 + (t - t_0)^2)^{(d+1)/2}}\delta(t_0)\tilde{p}(\boldsymbol{x}_0) d\boldsymbol{x}_0dt_0 \\
=&\, -\frac{1}{S_{d+1}(1)}\int\frac{(\boldsymbol{x} - \boldsymbol{x}_0, t)}{(\Vert\boldsymbol{x} - \boldsymbol{x}_0\Vert^2 + t^2)^{(d+1)/2}}\tilde{p}(\boldsymbol{x}_0) d\boldsymbol{x}_0 \\
\triangleq&\, (\boldsymbol{F}_{\boldsymbol{x}}, \boldsymbol{F}_t)
\end{aligned}\label{eq:field}\end{equation}
其中$\boldsymbol{F}_{\boldsymbol{x}}$是$\boldsymbol{F}(\boldsymbol{x}, t)$的前$d$个分量,$\boldsymbol{F}_t$是它的第$d+1$个分量。下一节我们再来讨论$\boldsymbol{F}(\boldsymbol{x}, t)$怎么学,现在假设$\boldsymbol{F}(\boldsymbol{x}, t)$已经知道了,那么接下来就是要沿着场线运动,也就是运动轨迹要时刻跟$\boldsymbol{F}(\boldsymbol{x}, t)$同方向,即
\begin{equation}(d\boldsymbol{x}, dt) = (\boldsymbol{F}_{\boldsymbol{x}}, \boldsymbol{F}_t) d\tau\quad\Rightarrow\quad \frac{d\boldsymbol{x}}{dt} = \frac{\boldsymbol{F}_{\boldsymbol{x}}}{\boldsymbol{F}_t}\label{eq:ode}\end{equation}
这就是生成过程所需要的微分方程(ODE)。在之前的$d$维方案中,除了有模式坍缩问题外,什么时候终止也是一个不好处理的细节问题。直观来想,就是沿着场线运动,直到撞上一个真实样本后就停止,但什么时候才是“撞上”,这个并不好判断。而在$d+1$维方案中,我们知道真实样本都是在$t=0$这个面上,所以可以很自然地以$t=0$为终止信号了。
至于初始分布,按照前面的讨论,应该是“半径足够大的、$d+1$维的球面均匀分布”,但既然我们是以$t=0$为终止信号,那么我们不妨固定一个足够大的$t=T$(大致是$40\sim 100$这个量级),然后在$t=T$这个平面上做采样,这样一来生成过程就变成了微分方程$\eqref{eq:ode}$从$t=T$到$t=0$的运动过程了,生成过程的始和终都变得相当明朗。
当然,如果在固定的$t=T$平面上采样,那肯定就不是均匀的了。事实上有:
\begin{equation}p_{prior}(\boldsymbol{x}) \propto \frac{1}{(\Vert\boldsymbol{x}\Vert^2 + T^2)^{(d+1)/2}}\end{equation}
推导过程见下面的框。可以看到,概率密度只依赖于模长$\Vert\boldsymbol{x}\Vert$,所以从该分布采样的方案是先按照特定的分布采样模长,然后再按均匀分布采样方向,将两者进行组合。对于模长的采样,记$r=\Vert\boldsymbol{x}\Vert$,我们将它换元到超球坐标,就可以得到$p_{prior}(r)\propto r^{d-1}(r^2 + T^2)^{-(d+1)/2}$,然后利用逆累积概率函数法进行采样就行了(参考《变分自编码器(七):球面上的VAE(vMF-VAE)》)。
初始分布的推导:场线是均匀穿过$d+1$维超球面上的,所以$(\boldsymbol{x}, T)$处的密度是反比于$S_{d+1}(\boldsymbol{x}, T)$,即$\propto \frac{1}{(\Vert\boldsymbol{x}\Vert^2 + T^2)^{d/2}}$,但现在不是在球面,而是在$t=T$的平面上,所以我们要将球面投影到平面上,示意图如下:
如上图,当$B$、$D$两点充分接近时,有$\Delta OAB\sim \Delta BDC$,所以
\begin{equation}\frac{|BC|}{|BD|} = \frac{|OB|}{|OA|} = \frac{\sqrt{\Vert\boldsymbol{x}\Vert^2 + T^2}}{T}\end{equation}
也就是说,原本球面上单位长度的弧,投影到平面上后长度变为了$\frac{\sqrt{\Vert\boldsymbol{x}\Vert^2 + T^2}}{T}$倍,由于只有一个维度变化,所以原来球面上的面积元,投影后也变为$\frac{\sqrt{\Vert\boldsymbol{x}\Vert^2 + T^2}}{T}$倍,因此根据概率反比面积,我们可以得到
\begin{equation}p_{prior}(\boldsymbol{x}) \propto \frac{1}{S_{d+1}(\boldsymbol{x}, T)}\times \frac{T}{\sqrt{\Vert\boldsymbol{x}\Vert^2 + T^2}}\propto \frac{1}{(\Vert\boldsymbol{x}\Vert^2 + T^2)^{(d+1)/2}}\end{equation}
场的训练 #
现在,初始分布有了,微分方程也有了,所以就只差向量场函数$\boldsymbol{F}(\boldsymbol{x}, t)$的训练了。从微分方程$\eqref{eq:ode}$可以看出,它只依赖于向量场的相对值,因此向量场的缩放不影响最终结果。根据式$\eqref{eq:field}$,向量场可以写为
\begin{equation}\boldsymbol{F}(\boldsymbol{x}, t) = \mathbb{E}_{\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0)}\left[-\frac{(\boldsymbol{x} - \boldsymbol{x}_0, t)}{(\Vert\boldsymbol{x} - \boldsymbol{x}_0\Vert^2 + t^2)^{(d+1)/2}}\right]\end{equation}
根据我们在《生成扩散模型漫谈(五):一般框架之SDE篇》、《生成扩散模型漫谈(七):最优扩散方差估计(上)》等文章多次用到一个结论:
\begin{equation}\mathbb{E}_{\boldsymbol{x}}[\boldsymbol{x}] = \mathop{\text{argmin}}_{\boldsymbol{\mu}}\mathbb{E}_{\boldsymbol{x}}\left[\Vert \boldsymbol{x} - \boldsymbol{\mu}\Vert^2\right]\end{equation}
我们可以引入函数$\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}, t)$来学习$\boldsymbol{F}(\boldsymbol{x}, t)$,训练目标为
\begin{equation}\mathbb{E}_{\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0)}\left[\left\Vert\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}, t) + \frac{(\boldsymbol{x} - \boldsymbol{x}_0, t)}{(\Vert\boldsymbol{x} - \boldsymbol{x}_0\Vert^2 + t^2)^{(d+1)/2}}\right\Vert^2\right]\label{eq:loss}\end{equation}
然而,上述目标的$\boldsymbol{x},t$还需要采样,它的采样方式没有明确定义。这就是PFGM的主要特点之一,它直接定义了反向过程(生成过程),不需要定义前向过程,而这一步的采样实际上就相当于前向过程。为此,原论文考虑地每个真实样本进行扰动的方式来构建$\boldsymbol{x},t$的样本:
\begin{equation}\boldsymbol{x} = \boldsymbol{x}_0 + \Vert \boldsymbol{\varepsilon}_{\boldsymbol{x}}\Vert (1+\tau)^m \boldsymbol{u},\quad t = |\varepsilon_t| (1+\tau)^m\end{equation}
其中$(\boldsymbol{\varepsilon}_{\boldsymbol{x}},\varepsilon_t)\sim\mathcal{N}(\boldsymbol{0}, \sigma^2\boldsymbol{I}_{(d+1)\times(d+1)})$,$m\sim U[0,M]$,$\boldsymbol{u}$是$d$维单位球面上均匀分布的单位向量,而$\tau,\sigma,M$则都是常数。这个设计有颇多的主观性,大家自行欣赏和领会即可,这里不做过多展开。后续讨论请看这里。
最后,原论文的训练目标跟本文的式$\eqref{eq:loss}$略有不同,大致相当于
\begin{equation}\left\Vert\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}, t) + \text{Normalize}\left(\mathbb{E}_{\boldsymbol{x}_0\sim \tilde{p}(\boldsymbol{x}_0)}\left[\frac{(\boldsymbol{x} - \boldsymbol{x}_0, t)}{(\Vert\boldsymbol{x} - \boldsymbol{x}_0\Vert^2 + t^2)^{(d+1)/2}}\right]\right)\right\Vert^2\end{equation}
实际训练时由于只能采样有限个$\boldsymbol{x}_0$对括号里边的期望进行估算,因此该目标实际上是一个有偏估计。当然有偏不一定就比无偏更差,具体为什么原论文使用有偏估计,这里暂时不得而知,猜测是因为有偏估计由于对向量进行了归一化操作,可能会使得训练进程更加稳定,但是也因为有偏的估计进行了归一化,所以需要较大的batch_size才能比较准,这对实验成本提了要求。
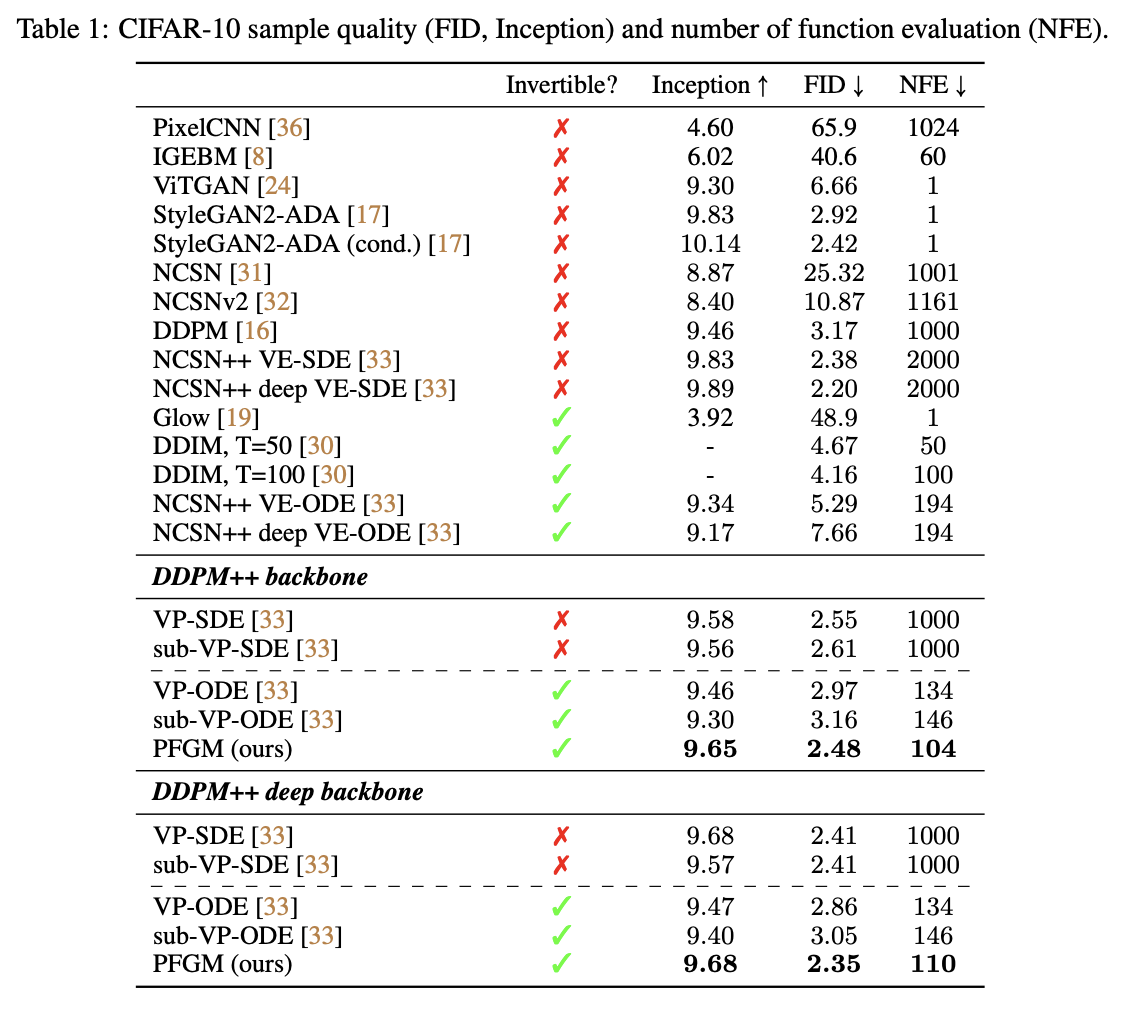
实验结果 #
可以说,PFGM是一个彻底的新框架,它不再像之前一样依赖于高斯假设,并且得到了一个确实有着全新内涵的模型。然而,我们不能“为新而新”,如果新的框架没有做出更有说服力的结果,那么新就是没有意义的。
当然,原论文的实验结果,肯定了PFGM的价值,比如得到了更好的评估指标、更快的生成速度,以及对超参数(包括模型架构)有更好的鲁棒性等,这里就不一一展示了,大家自行读原论文就好。我看了看原论文中了NeurIPS 2022,不得不说这确实是实至名归的顶会论文啊!
文章小结 #
本文介绍了一个由“万有引力定律”启发的ODE式扩散模型,它突破了以往众多扩散模型对高斯假设的依赖,是一个基于场论来构建ODE式扩散模型的全新框架,整个模型颇多启发性,值得仔细研读。
转载到请包括本文地址:https://kexue.fm/archives/9305
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Oct. 18, 2022). 《生成扩散模型漫谈(十三):从万有引力到扩散模型 》[Blog post]. Retrieved from https://kexue.fm/archives/9305
@online{kexuefm-9305,
title={生成扩散模型漫谈(十三):从万有引力到扩散模型},
author={苏剑林},
year={2022},
month={Oct},
url={\url{https://kexue.fm/archives/9305}},
}










October 18th, 2022
看了一下作者们,果然是有物理背景的,这文章真是绝了
October 20th, 2022
老实说,这几位作者github上的代码真是太复杂了……
想做点应用,但头都撸秃了都搞不定……
October 20th, 2022
感觉公式(10)那里有点问题……
论文在附录B.1.1里只给出了M的下界,意思似乎是M足够大就可以。
那么不妨取附录给出的超参(τ=0.03,M=291),$||t_i||$最大可达$(τ+1)^M=5400$。论文中给出了∣∣y∣∣ ≈ 3000的实例。
则(10)分母部分可达$5400^{d+1}$,很轻松就爆了……
这个简单啊,它是分母啊,写成乘以$(\Vert\boldsymbol{x} - \boldsymbol{x}_0\Vert^2 + t^2)^{-(d+1)/2}$,不就好了吗~
October 27th, 2022
感谢分享!!!
November 10th, 2022
感觉沿着这个思路 是不是gravity这种反比率其实并不重要?也就是说其实我们能够任意定义某个data-dependent的continuous flow: F(x, t|x0) 并让它满足一些条件比如从任意点出发最后都会收敛到x0/随着t减小F变大(?)等等
原始的DDIM是不是也可以从类似的思路出发 首先得到continuous flow 然后再用neuralnet去逼近
理论上确实引力这种反比律并不是唯一适合的,应该有更多的方案,我也试图构建一个一般框架,但是卡在了一步推导过不去,正在努力中。
整个score sde的框架应该都是可以从neural ODE里面弄出来好像。
最近有个博士论文讲neural ODE就提到了continuous normalizing flow, neural SDE这些东西
其他我都有所耳闻,ode推出sde我倒是没听说过。
不好意思我表述得不清楚
应该没有推出,只是扩展成SDE,就给原本的加上一个stochastic term~
是这个https://arxiv.org/abs/2202.02435,不知道你看过没
博士论文一般偏综述,通常很少看。
July 1st, 2023
(5)式,(7)式分子应该都是T吧?
不是$\propto$了吗?
July 18th, 2023
苏神,这里说的模式坍塌我不太理解。
对于包含源在内的一个任意球壳积分,内部引力源确实是相当于消失了。但是本方法中,需要考虑的不是点的问题吗?任意一个点所受的引力,除非正好训练集在这里的引力抵消,否则都是存在着的。那么此时其所受引力方向不就是场线方向吗?
其实我最近思考ddpm生成能力问题时,就产生了一个想法,ddpm训练过程,对于某个点来说,相当于就是各个训练集中的引力源(也就是训练图)在给这个点以引力,而这个点最终训练结果就是众多不同训练图对它产生的合力。 ddpm依赖于模型的平滑性,在训练中为全像素空间的点都提供了大致的引力方向,引导任意的初始点往训练图所在的流形靠近。不知道这样去理解是否是错误的呢。
因为在此理解下,我以为添加文字控制时,就需要控制各个文字对应的编码要在图像语义上接近。否则这种引力引导就可能出错。而这一点和sd采用clip就正好对应上了,clip的文字语义相近时在图像语义上也接近。
你都说“除非正好训练集在这里的引力抵消”了,模式坍缩就是“除非”的后果。也许你觉得没有那么巧正好完全抵消,但事实上即便抵消一部分,也是丧失一部分多样性。从直观理解的角度,粗糙一点无所谓,而从理论构建的角度来看,就是要严格杜绝这种可能性。
May 9th, 2024
苏神,我觉得第(8)式有点疑问:虽然是在$d+1$维,但是平面$t=0$上受的引力应该不变,但是根据(8),分母的幂次从$d/2$ 变成了$(d+1)/2$。要怎么理解?
这里是指$t,\boldsymbol{x}$视为一个整体的$d+1$维“空间”,而不是像相对论那样只是形式上把$t,\boldsymbol{x}$视为$d+1$维“时空”,$d+1$维空间中的引力大小与距离的$d$次方成反比。
November 19th, 2025
苏神,能多发点这种物理和机器学习结合的研究内容吗?或者您觉得机器学习在物理研究当中作用大吗?现在比较火的方向,代理模型之类的,物理信息神经网络这些有研究价值吗?
我自己没特别关注这种物理景观特别明显的研究,或者说这类研究真正明显work的似乎不多。