莱昂哈德·欧拉

莱昂哈德·欧拉

作为数学史上最高产的数学家（似乎没有之一），欧拉的研究几乎涉及了所有数学领域，包括数论、图论、微积分等，同时他还是一个物理学家，他与拉格朗日首创的变分法使得经典力学的研究达到了一个新的高度。欧拉具有惊人的计算能力和数学直觉，这对他的数学研究帮助极大。现在在很多领域，我们都可以看到不少以欧拉命名的公式、定理。欧拉在数学上极为高产，而且得出了相当多的正确结论，但其中有相当多的结论只是来源于他的数学直觉（创造性思维）以及类比推理，这并非欧拉不追求严谨，而是由于当时数学知识的局限性，难以严密化。还有，研究的顺序是：先得出答案，然后才论证答案！

再者，创造性思维往往令人叫绝，能更加促进我们的思维能力。过多地考虑严格性和技术细节，通常都妨碍了我们得出正确的答案。正如《解题的艺术》中说道：粗略而有灵感的思想可能会引出严格证明；而有时，严格的证明会完全淡化论证的精髓。因此，我们不必在意欧拉证明的不严谨，反而，它是一次完美的视觉与思维享受。正因如此，一些绝妙、非严密、（在某种程度上）不正确的但同时得出了正确结果的数学论证，就被称为“欧拉数学”。事实上，任何人、任何研究都必须经过“欧拉数学”这一不严密的早期阶段。

------------华丽的分割线----------------

下面是一条关于凸多面体的面、顶、棱公式，它属于拓扑学的内容，我们称之为“欧拉公式”。（当然，公式是欧拉的，论证过程只是笔者粗糙地给出的）。

欧拉发现，对于任意凸多面体，其顶点数(v)、棱边数(e)、面数(f)有着以下关系：v-e+f=2

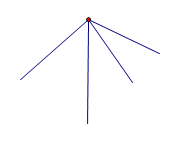
欧拉公式1

欧拉公式1

为什么会有这样的关系呢？（一）首先我们单纯来考察一个点的情况。如图，一个点可以作出n条射线，这n条射线组成了n个凸面，此时v-e+f=1-n+n=1=常数，这就暗示我们，任意多面体的v、e、f之间可能会有类似的不变关系。

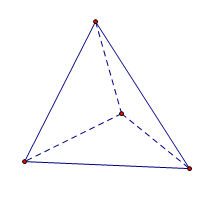
欧拉公式2

欧拉公式2

现在来考察任意的四面体，如图，不难统计出对于四面体，有v-e+f=2。在平面上，三角形是一切多边形的“组成单元”（即每个多边形可以划分为若干个不重叠的三角形，这是推导多边形内角和公式的前提）；类似的，在空间中，四面体是一切多面体（至少是凸多面体）的“组成单元”，因此，对于任意的n面体，我们可以将其划分为(n-3)个四面体。

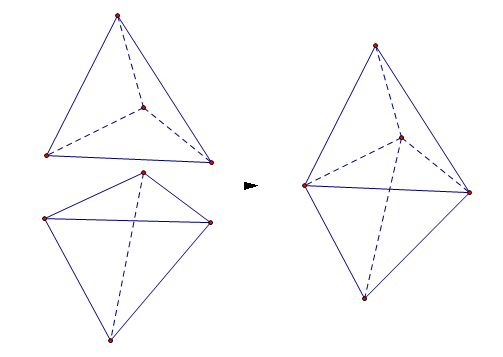
现在考虑将这些四面体“碎片”组合成原来的n面体会发生什么。只考虑两个四面体拼接在一起的情况：两个独立的四面体，必然有v-e+f=4；同时，这两个四面体必然有一个面全等，将这两个面“对接”，无疑，我们失去了2个面、3个点以及3条棱，这样实际上有v-e+f=4-2+3-3=2，关系保持不变。当然，有可能出现两个侧面拼成了一个面的情况，此时我们将再“失去”了1个面和1条棱，v-e+f=2依然成立！

欧拉公式3

欧拉公式3

因此，再继续拼接下去，关系v-e+f=2在拼接过程中保持不变，所以欧拉公式对于任意多面体成立！

------------华丽的分割线----------------

以上是对于欧拉公式的一个粗糙的讨论，当然它只是一次思维的体操，而并非严格的论证。但正如本文开头所说，我们更应该热衷于创造性探索，而不是枯燥无味的细节。因为创造性是一种美感，一种心灵的触动，它从深处触动了我们热爱数学、探索数学的心。这也正是“欧拉数学”的魅力所在！

转载到请包括本文地址：https://kexue.fm/archives/1496

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Nov. 17, 2011). 《[欧拉数学]凸多面体的面、顶、棱公式 》[Blog post]. Retrieved from https://kexue.fm/archives/1496

@online{kexuefm-1496,
        title={[欧拉数学]凸多面体的面、顶、棱公式},
        author={苏剑林},
        year={2011},
        month={Nov},
        url={\url{https://kexue.fm/archives/1496}},
}