级联抑制：提升GAN表现的一种简单有效的方法

昨天刷arxiv时发现了一篇来自星星韩国的论文，名字很直白，就叫做《A Simple yet Effective Way for Improving the Performance of GANs》。打开一看，发现内容也很简练，就是提出了一种加强GAN的判别器的方法，能让GAN的生成指标有一定的提升。

作者把这个方法叫做Cascading Rejection，我不知道咋翻译，扔到百度翻译里边显示“级联抑制”，想想看好像是有这么点味道，就暂时这样叫着了。介绍这个方法倒不是因为它有多强大，而是觉得它的几何意义很有趣，而且似乎有一定的启发性。

正交分解 #

GAN的判别器一般是经过多层卷积后，通过flatten或pool得到一个固定长度的向量$\boldsymbol{v}$，然后再与一个权重向量$\boldsymbol{w}$做内积，得到一个标量打分（先不考虑偏置项和激活函数等末节）：
\begin{equation}D(\boldsymbol{x})=\langle \boldsymbol{v},\boldsymbol{w}\rangle\end{equation}
也就是说，用$\boldsymbol{v}$作为输入图片的表征，然后通过$\boldsymbol{v}$和$\boldsymbol{w}$的内积大小来判断出这个图片的“真”的程度。

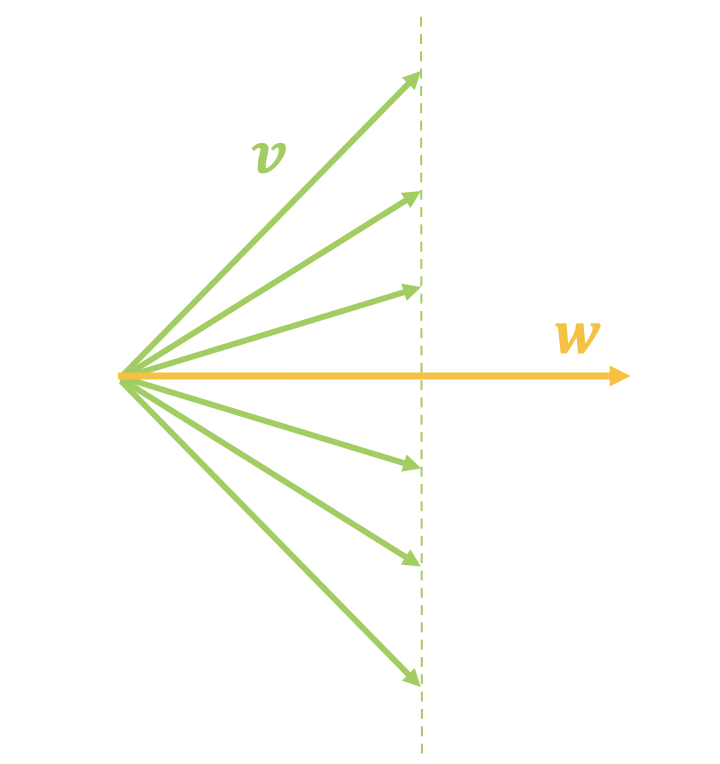
然而，$\langle \boldsymbol{v},\boldsymbol{w}\rangle$只取决于$\boldsymbol{v}$在$\boldsymbol{w}$上的投影分量，换言之，固定$\langle \boldsymbol{v},\boldsymbol{w}\rangle$和$\boldsymbol{w}$时，$\boldsymbol{v}$仍然可以有很大的变动，如下面左图所示。

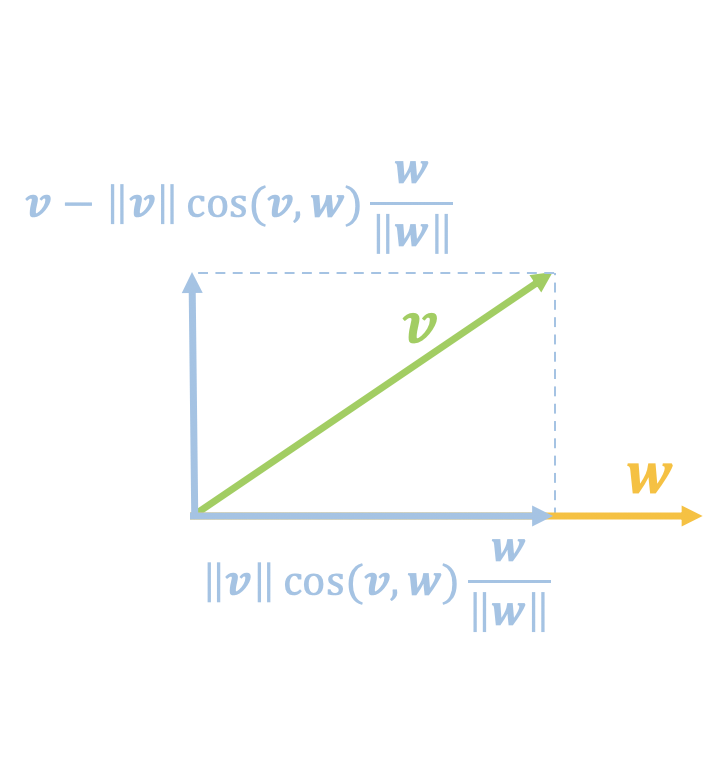
假如我们认为$\langle \boldsymbol{v},\boldsymbol{w}\rangle$等于某个值时图片就为真，问题是$\boldsymbol{v}$变化那么大，难道每一个$\boldsymbol{v}$都代表一张真实图片吗？显然不一定。这就反映了通过内积来打分的问题所在：它只考虑了在$\boldsymbol{w}$上的投影分量，没有考虑垂直分量（如上面右图）：
\begin{equation}\boldsymbol{v}-\Vert \boldsymbol{v}\Vert \cos(\boldsymbol{v},\boldsymbol{w}) \frac{\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert}=\boldsymbol{v}- \frac{\langle\boldsymbol{v},\boldsymbol{w}\rangle}{\Vert \boldsymbol{w}\Vert^2}\boldsymbol{w}\end{equation}

既然如此，一个很自然的想法是：能否用另一个参数向量来对这个垂直分量在做一次分类呢？显然是可以的，而且这个垂直分量的再次分类时也会导致一个新的垂直分量，因此这个过程可以迭代下去：
\begin{equation}\left\{\begin{aligned}&\boldsymbol{v}_1=\boldsymbol{v}\\
&D_1(\boldsymbol{x})=\langle \boldsymbol{v}_1,\boldsymbol{w}_1\rangle\\
&\boldsymbol{v}_2 = \boldsymbol{v}_1- \frac{\langle\boldsymbol{v}_1,\boldsymbol{w}_1\rangle}{\Vert \boldsymbol{w}_1\Vert^2}\boldsymbol{w}_1\\
&D_2(\boldsymbol{x})=\langle \boldsymbol{v}_2,\boldsymbol{w}_2\rangle\\
&\boldsymbol{v}_3 = \boldsymbol{v}_2- \frac{\langle\boldsymbol{v}_2,\boldsymbol{w}_2\rangle}{\Vert \boldsymbol{w}_2\Vert^2}\boldsymbol{w}_2\\
&D_3(\boldsymbol{x})=\langle \boldsymbol{v}_3,\boldsymbol{w}_3\rangle\\
&\boldsymbol{v}_4 = \boldsymbol{v}_3- \frac{\langle\boldsymbol{v}_3,\boldsymbol{w}_3\rangle}{\Vert \boldsymbol{w}_3\Vert^2}\boldsymbol{w}_3\\
&\qquad\vdots\\
&D_N(\boldsymbol{x})=\langle \boldsymbol{v}_N,\boldsymbol{w}_N\rangle\\
\end{aligned}\right.\end{equation}

分析思考 #

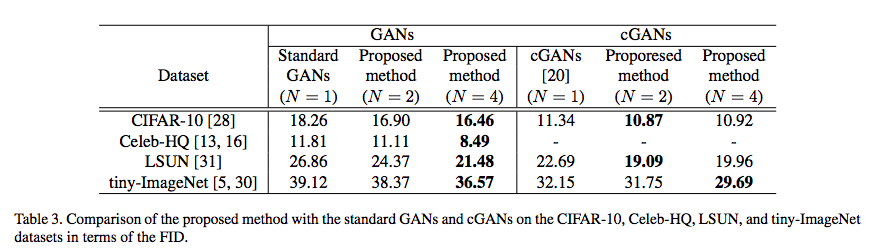
其实写到这，原论文的思路基本上已经说完了，剩下的是一些细节上的操作。首先已经有了$N$个打分$D_1(\boldsymbol{x}),D_2(\boldsymbol{x}),\dots,D_N(\boldsymbol{x})$，每个打分都可以应用判别器的loss（直接用hinge loss或者加sigmoid激活后用交叉熵），最后对这$N$个loss加权平均，作为最终的判别器loss，仅这样就能带来GAN的性能提升了。作者还将其进一步推广到CGAN中，也得到了不错的效果。

相比实验结果，笔者认为这个技巧更深层次的意义更值得关注。其实这个思路可以按理说可以用到一般的分类问题中而不单单是GAN。由于把垂直分量都迭代地加入了预测，我们可以认为参数$\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_N$分别代表了$N$个不同的视角，而每一个分类相当于在不同的视角下进行分类判断。

想到这里，笔者想起了Hinton的Capsule。虽然形式上不大一样，但本意上似乎有相通之处，Capsule希望用一个向量而不是标量来表示一个实体，这里的“级联抑制”也是通过不断进行垂直分解来给出多个角度的分类结果，也就是说认定一个向量是不是属于一个类，必须给出多个打分而不单是一个，这也有“用向量而不是标量”的味道。

遗憾的是，笔者按上述思路简单实验了一下（cifar10），发现验证集的分类准确率下降了一点（注意这跟GAN的结果不矛盾，提升GAN的表现是因为加大了判别难度，但是有监督的分类模型不希望加大判别难度），但是好在过拟合程度也减少了（即训练集和验证集的准确率差距减少了），当然笔者的实验过于简陋，不能做到严谨地下结论。不过笔者依然觉得，由于其鲜明的几何意义，这个技巧仍然值得进一步思考。

文章小结 #

本文介绍了一个具有鲜明几何意义的提升GAN表现的技巧，并且进一步讨论了它进一步的潜在价值。

转载到请包括本文地址：https://kexue.fm/archives/7105

更详细的转载事宜请参考：《科学空间FAQ》