从三角不等式到Margin Softmax

在《基于GRU和AM-Softmax的句子相似度模型》中我们介绍了AM-Softmax，它是一种带margin的softmax，通常用于用分类做检索的场景。当时通过图示的方式简单说了一下引入margin是因为“分类与排序的不等价性”，但没有比较定量地解释这种不等价性的来源。

在这篇文章里，我们来重提这个话题，从距离的三角不等式的角度来推导和理解margin的必要性。

三角不等式 #

平时，我们说的距离一般指比较直观的“欧氏距离”，但在数学上距离，距离又叫“度量”，它有公理化的定义，是指定义在某个集合上的二元函数$d(x,y)$，满足：

1、非负性：$d(x,y)\geq 0$；

2、同一性：$d(x,y)=0\Leftrightarrow x = y$；

3、对称性：$d(x,y)=d(y,x)$；

4、三角不等式：$d(x,y)\leq d(x,z) + d(z,y)$。

顾名思义，距离是用来度量$x,y$之间的差异程度的。理论上来说，只要满足前两点要求，就可以用来度量差异了，比如概率里边常用的KL散度，就仅仅满足前两点。第3、4点的加入，本质上来说是为了使得这样定义出来的距离与我们常见的欧氏距离更加接近，比如对称性是“距离没有方向”的体现，而三角不等式是“两点之间直线最短”的体现，这些类似有利于我们通过欧氏距离的类比来思考更一般的距离。

从这个定义来看，深度学习其实比较少碰到符合上述4点要求的距离，比如通常的分类是直接用内积加softmax，而内积只满足第三点；余弦距离$1-\cos(x,y)$也只满足第1、3点，不满足第2、4点，如果我们将所有同方向的向量视为相等向量的话，那么它也算是满足第2点。

不过，某些函数我们可以微调一下定义，使得它成为一个距离，比如我们知道欧氏距离是满足三角不等式的，所以
\begin{equation}\left\Vert \frac{x}{\Vert x\Vert} - \frac{y}{\Vert y\Vert}\right\Vert = \sqrt{2 - 2\cos(x,y)}\end{equation}
必然也满足三角不等式。所以，余弦距离$1-\cos(x,y)$是不满足三角不等式的，但是改为$\sqrt{1-\cos(x,y)}$就满足了。

分类与排序 #

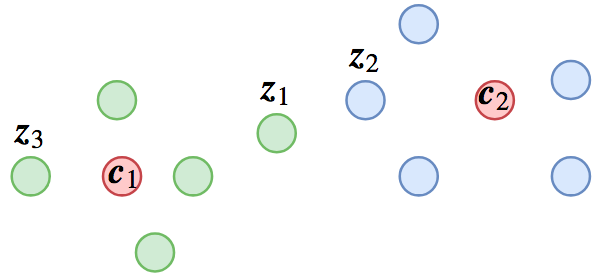
像人脸识别或者句子相似度等场景，在预测阶段我们是拿特征去排序的，我们自然希望随便拿一个样本，就能够检索出所有同类样本，这就要求“类内差距小于类间差距”；但是，如果我们将其作为分类任务训练的话，则未必能达到这个目的，因为分类任务的目标是“最靠近所属类的中心”。具体例子可以参考下图：

在该图中，$z_1,z_3$属于类$c_1$，$z_2$输于类$c_2$，从分类角度来看$d(z_1, c_1) < d(z_1, c_2)$、$d(z_2, c_2) < d(z_2, c_1)$，因此分类都是正确的，但是$d(z_1, z_2) < d(z_1, z_3)$，所以用$z_1$去检索的话，找到的是不同类的$z_2$，而不是同类的$z_3$。

我们可以通过三角不等式更加定量地描述这种不等关系：我们希望达到$d(z_1, z_3) < d(z_1, z_2)$，根据三角不等式有$d(z_1,z_3)\leq d(z_1, c_1) + d(z_3, c_1)$，所以一个充分的条件是
\begin{equation}d(z_1, c_1) + d(z_3, c_1) < d(z_1, z_2) \end{equation}
两端加上$d(z_2, c_2)$，并利用三角不等式$d(z_1, z_2) + d(z_2, c_2)\geq d(z_1, c_2)$，我们得到上式的一个充分条件是
\begin{equation}d(z_1, c_1) + d(z_3, c_1) + d(z_2, c_2) < d(z_1, c_2) \end{equation}
要注意的是，分类任务只要求对于$z_1$来说有$d(z_1, c_1) < d(z_1, c_2)$，而上式多出了$d(z_3, c_1) + d(z_2, c_2)$，多出来的一项就是margin项。

注意到$d(z_3, c_1),d(z_2, c_2)$分别是样本$z_3,z_2$到其所属类中心的距离，所以我们可以认为$d(z_3, c_1) + d(z_2, c_2)$是“类平均直径”，它应该接近一个常数$m$，我们可以将它作为超参数调整。如果要自适应调整的话，可以考虑先$m=0$训练一段时间，然后估计“类平均直径”作为$m$再训练，然后再重新估计$m$并训练，等等。

AM-Softmax #

通过上面的推导，我们知道为了保证分类模型的特征可以用于排序，那么每个样本不仅仅要最靠近类中心，而且是距离加上$m$之后还要最靠近类中心，即如果$z_1$属于类$c_1$的话，那么就要求：
\begin{equation}\begin{aligned}
d(z_1, c_1) +&\, m < d(z_1, c_2) \\
d(z_1, c_1) +&\, m < d(z_1, c_3) \\
&\vdots \\
d(z_1, c_1) +&\, m < d(z_1, c_k)
\end{aligned}\end{equation}
根据《将“Softmax+交叉熵”推广到多标签分类问题》里边的思路：只要我们希望$s_i < s_j$，就可以往$\log$里边加入$e^{s_i - s_j}$来构造loss。所以我们就可以构造如下的loss：
\begin{equation}\log\left(1+\sum_{i=2}^k e^{s\cdot[d(z_1, c_1) + m - d(z_1, c_i)]}\right)\end{equation}
这便是带加性margin的交叉熵，其中$s$是缩放比例，相当于softmax的温度参数。

不过别忘了，上述推导都是基于$d$满足三角不等式，而我们平常用的打分函数并不满足三角不等式。对于训练检索模型来说，我们通常用余弦距离来打分，前面说了余弦距离可以通过开根号来满足三角不等式，所以对应的要求变为（以$i=2$为例）：
\begin{equation}\begin{array}{c}
\sqrt{1-\cos(z_1, c_1)} + m < \sqrt{1-\cos(z_1, c_2)}\\
\Downarrow\\
\sqrt{1-\cos(z_1, c_2)} - \sqrt{1-\cos(z_1, c_1)} > m \\
\end{array}\end{equation}
两边乘以$\sqrt{1-\cos(z_1, c_2)} + \sqrt{1-\cos(z_1, c_1)}$得到
\begin{equation}\cos(z_1, c_1) - \cos(z_1, c_2) > m\left(\sqrt{1-\cos(z_1, c_2)} + \sqrt{1-\cos(z_1, c_1)}\right)\end{equation}
显然右端是有上界的，所以适当调整$m$，可以使得
\begin{equation}\cos(z_1, c_1) - \cos(z_1, c_2) > m\end{equation}
成为一个充分条件，这时候对应的margin交叉熵是
\begin{equation}\log\left(1+\sum_{i=2}^k e^{s\cdot[\cos(z_1, c_i) + m - \cos(z_1, c_1)]}\right)\end{equation}
这就是AM-Softmax。

回顾与小结 #

本文从三角不等式的角度推导了用分类模型做排序任务时margin的必要性，假定所用的打分函数满足三角不等式的前提下，能比较自然地导出相关结果。

转载到请包括本文地址：https://kexue.fm/archives/8656

更详细的转载事宜请参考：《科学空间FAQ》