EMO：基于最优传输思想设计的分类损失函数

众所周知，分类任务的标准损失是交叉熵（Cross Entropy，等价于最大似然MLE，即Maximum Likelihood Estimation），它有着简单高效的特点，但在某些场景下也暴露出一些问题，如偏离评价指标、过度自信等，相应的改进工作也有很多，此前我们也介绍过一些，比如《再谈类别不平衡问题：调节权重与魔改Loss的对比联系》、《如何训练你的准确率？》、《缓解交叉熵过度自信的一个简明方案》等。由于LLM的训练也可以理解为逐token的分类任务，默认损失也是交叉熵，因此这些改进工作在LLM流行的今天依然有一定的价值。

在这篇文章中，我们介绍一篇名为《EMO: Earth Mover Distance Optimization for Auto-Regressive Language Modeling》的工作，它基于最优传输思想提出了新的改进损失函数EMO，声称能大幅提高LLM的微调效果。其中细节如何？让我们一探究竟。

概率散度 #

假设$p_i$是模型预测的第$i$个类别的概率，$i=1,2,\cdots,n$，$t$则是目标类别，那么交叉熵损失为
\begin{equation}\mathcal{L} = - \log p_t\end{equation}
如果将标签$t$用one hot形式的分布$\tau$表示出来（即$\tau_t=1,\tau_i=0|i\neq t, i\in[1,n]$），那么它可以重写成
\begin{equation}\mathcal{L} = - \sum_i \tau_i\log p_i\end{equation}
这个形式同时适用于非one hot的标签$\tau$（即软标签），它等价于优化$\tau,p$的KL散度：
\begin{equation}KL(\tau\Vert p) = \sum_i \tau_i\log \frac{\tau_i}{p_i} = \color{skyblue}{\sum_i \tau_i\log \tau_i} - \sum_i \tau_i\log p_i\end{equation}
当$\tau$给定时，最右端第一项就是一个常数，所以它跟交叉熵目标是等价的。

这个结果表明，我们在做MLE，或者说以交叉熵为损失时，实则就是在最小化目标分布和预测分布的KL散度。由于KL散度的一般推广是f散度（参考《f-GAN简介：GAN模型的生产车间》），所以很自然想到换用其他f散度或许有改良作用。事实上，确实有不少工作是按照这个思路进行的，比如《缓解交叉熵过度自信的一个简明方案》介绍的方法，其论文的出发点是“Total Variation距离”，也是f散度的一种。

最优传输 #

不过，每种f散度或多或少有些问题，要说概率分布之间的理想度量，当属基于最优传输思想的“推土机距离（Earth Mover's Distance，EMD）”，不了解的读者可以参考一下笔者之前写的《从Wasserstein距离、对偶理论到WGAN》。

简单来说，推土机距离定义为两个分布之间的最优传输成本：
\begin{equation}\mathcal{C}[p,\tau]=\inf_{\gamma\in \Pi[p,\tau]} \sum_{i,j} \gamma_{i,j} c_{i,j} \end{equation}
这里的$\gamma\in \Pi[p,\tau]$说的是$\gamma$是任意以$p,\tau$为边缘分布的联合分布，$c_{i,j}$是实现给定的成本函数，代表“从$i$搬运到$j$的成本”，$\inf$是下确界，意思就是说将最低的运输成本作为$p,\tau$之间的差异度量。正如基于f散度的Vanilla GAN换成基于最优传输的Wasserstein GAN能够更好的收敛性质，我们期望如果将分类的损失函数换成两个分布的W距离，也能收敛到更好的结果。

当$\tau$是one hot分布时，目标分布就是一个点$t$，那么就无所谓最不最优了，传输方案就只有一个，即把$p$的所有东西都搬到同一个点$t$，所以此时就有
\begin{equation}\mathcal{C}[p,\tau]= \sum_i p_i c_{i,t} \label{eq:emo}\end{equation}

如果$\tau$是一般的软标签分布，那么$\mathcal{C}[p,\tau]$的计算是一个线性规划问题，求解起来比较复杂，由于$p_i \tau_j$所定义的分布也属于$\Pi[p,\tau]$，那么我们有
\begin{equation}\mathcal{C}[p,\tau]=\inf_{\gamma\in \Pi[p,\tau]} \sum_{i,j} \gamma_{i,j} c_{i,j} \leq \sum_{i,j} p_i \tau_j c_{i,j} \end{equation}
这是一个容易计算的上界，也可以作为优化目标，式$\eqref{eq:emo}$则对应$\tau_j = \delta_{j,t}$，其中$\delta$是“克罗内克δ函数”。

成本函数 #

现在回到原论文所关心的场景——LLM的微调，包括二次预训练和微调到下游任务等。正如本文开头所述，LLM的训练可以理解为逐token的分类任务（类别即所有token），每个标签是one hot的，所以适用于式$\eqref{eq:emo}$。

式$\eqref{eq:emo}$还差成本函数$c_{i,t}$还没定下来。如果简单地认为只要$i\neq t$，那么成本都是1，即$c_{i,t}=1 - \delta_{i,t}$，那么
\begin{equation}\mathcal{C}[p,\tau]= \sum_i p_i c_{i,t} = \sum_i (p_i - p_i \delta_{i, t}) = 1 - p_t\end{equation}
这其实就是在最大化准确率的光滑近似（参考《函数光滑化杂谈：不可导函数的可导逼近》）。但直觉上，所有$i\neq t$都给予同样程度的惩罚似乎过于简单了，理想情况下应该根据相似度来给每个不同的$i$设计不同的成本，即相似度越大，传输成本越低，那么我们可以将传输成本设计为
\begin{equation}c_{i,t} = 1 - \cos(\boldsymbol{e}_i,\boldsymbol{e}_t) = 1 - \left\langle\frac{\boldsymbol{e}_i}{\Vert\boldsymbol{e}_i\Vert}, \frac{\boldsymbol{e}_t}{\Vert\boldsymbol{e}_t\Vert}\right\rangle\end{equation}
这里的$\boldsymbol{e}_i,\boldsymbol{e}_t$是事先获取到Token Embedding，原论文是将预训练模型的LM Head作为Token Embedding的，并且根据最优传输的定义成本函数是要实现给定的，因此计算相似度的Token Embedding要在训练过程中固定不变。

有了成本函数后，我们就可以计算
\begin{equation}\mathcal{C}[p,\tau]= \sum_i p_i c_{i,t} = \sum_i \left(p_i - p_i \left\langle\frac{\boldsymbol{e}_i}{\Vert\boldsymbol{e}_i\Vert}, \frac{\boldsymbol{e}_t}{\Vert\boldsymbol{e}_t\Vert}\right\rangle\right) = 1 - \left\langle \sum_i p_i \frac{\boldsymbol{e}_i}{\Vert\boldsymbol{e}_i\Vert}, \frac{\boldsymbol{e}_t}{\Vert\boldsymbol{e}_t\Vert}\right\rangle\end{equation}
这就是EMO（Earth Mover Distance Optimization）最终的训练损失。由于embedding_size通常远小于vocab_size，所以先算$\sum\limits_i p_i \frac{\boldsymbol{e}_i}{\Vert\boldsymbol{e}_i\Vert}$能明显降低计算量。

实验效果 #

由于笔者对LLM的研究还处于预训练阶段，还未涉及到微调，所以暂时没有自己的实验结果，只能先跟大家一起看看原论文的实验。不得不说，原论文的实验结果还是比较惊艳的。

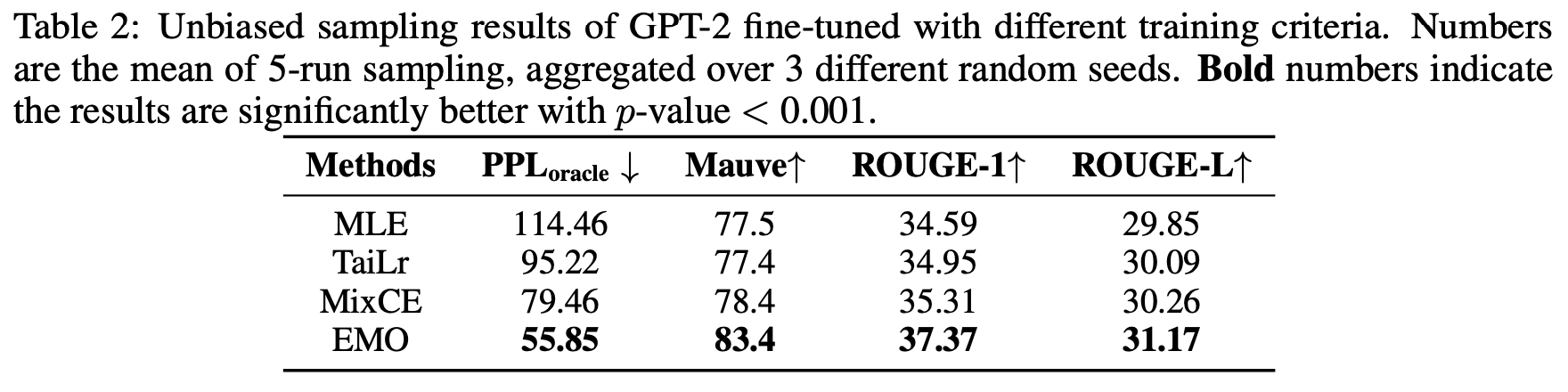
首先，是小模型上的继续预训练实验，相比交叉熵（MLE）的提升最多的有10个点，并且是全面SOTA：

小模型上的继续预训练对比实验

值得一提的是，这里的评价指标是MAUVE，越大越好，它提出自《MAUVE: Measuring the Gap Between Neural Text and Human Text using Divergence Frontiers》，是跟人工评价最相关的自动评测指标之一。此外，对比方法的TaiLr我们曾在《缓解交叉熵过度自信的一个简明方案》简单介绍过。

可能有读者想EMO更好是不是单纯因为评价指标选得好？并不是，让人意外的是，EMO训练的模型，甚至PPL都更好（PPL跟MLE更相关）：

不同评价指标的对比

然后是将LLAMA-7B/13B微调到下游任务做Few Shot的效果，同样很出色：

LLAMA-7B:13B微调到下游任务的效果

最后对比了不同模型规模和数据规模的效果，显示出EMO在不同模型和数据规模上都有不错的表现：

不同模型规模/数据规模上的效果

个人思考 #

总的来说，原论文的“成绩单”还是非常漂亮的，值得一试。唯一的疑虑可能是原论文的实验数据量其实都不算大，不清楚进一步增大数据量后是否会缩小EMO和MLE的差距。

就笔者看来，EMO之所以能取得更好的结果，是因为它通过Embedding算相似度，来为“近义词”分配了更合理的损失，从而使得模型的学习更加合理。因为虽然形式上LLM也是分类任务，但它并不是一个简单的对与错问题，并不是说下一个预测的token跟标签token不一致，句子就不合理了，因此引入语义上的相似度来设计损失对LLM的训练是有帮助的。可以进一步猜测的是，vocab_size越大、token颗粒度越大的情况下，EMO的效果应该越好，因为vocab_size大了“近义词”就可能越多。

当然，引入语义相似度也导致了EMO不适用于从零训练，因为它需要一个训练好的LM Head作为Token Embedding。当然，一个可能的解决方案是考虑用其他方式，比如经典的Word2Vec来事先训练好Token Embedding，但这可能会有一个风险，即经典方式训练的Token Embedding是否会降低LLM能力的天花板（毕竟存在不一致性）。

此外，即便Token Embedding没问题，从零预训练时单纯用EMO可能还存在收敛过慢的问题，这是因为根据笔者在《如何训练你的准确率？》的末尾提出的损失函数视角：

首先寻找评测指标的一个光滑近似，最好能表达成每个样本的期望形式，然后将错误方向的误差逐渐拉到无穷大（保证模型能更关注错误样本），但同时在正确方向保证与原始形式是一阶近似。

也就是说，为了保证（从零训练的）收敛速度，错误方向的损失最好能拉到无穷大，而EMO显然不满足这一点，因此将EMO用于从零训练的时候，大概率是EMO与MLE的某个加权组合，才能平衡收敛速度和最终效果。

文章小结 #

本文介绍了交叉熵损失的一个新的“替代品”——基于最优传输思想的EMO，与以往的小提升不同，EMO在LLM的微调实验中取得了较为明显的提升。

转载到请包括本文地址：https://kexue.fm/archives/9797

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。