谈大气消光和大气折光

苏剑林（BoJone） 编写/翻译

实际感受：

大家也许会有这样的生活经验：早上的太阳没有中午的太阳猛烈？从东方升起到我们的头顶，月亮一直在变“亮”？……这些现象都与地球大气的“消光”现象密切相关！

众所周知，地球有一层厚厚的大气，既是我们呼吸的来源，也是我们生命的保护伞。他为我们提供了臭氧层，也为我们提供了蓝天和风霜雨露，还为我们送上了绚丽的彩虹。然而，在天文学角度，大气却是我们的“障碍”，浓厚的大气不利于我们对宇宙进行清晰的观测。因此，天文学家们一直希望把天文台建立海拔更高的地方，因为那里有着稀薄的大气……为了渴求更高的清晰度，人们甚至把望远镜放到了地球之外。

地球大气对观测的影响主要表现为两个方面：一个是大气消光，一个是大气折光（似乎也是天文奥赛喜欢出的题目）。前者是指大气对光线的削弱作用，早晨的太阳没有那么亮也是这个原因；后者是指大气对光线的偏折作用，例如我们看到落日在地平线的最后一瞬间，实际上太阳早已落到了地平线之下了。

大气消光：

“消光”是指天体辐射在被观测者接收到它的光线前的过程中，受到一系列的影响而使天体辐射强度减弱。在光线的传播途中，主要受到星际消光和大气消光（哈勃空间望远镜没有大气消光问题）的影响。在天体测量中，任何一种消光影响都不可忽略。

在地球表面上观测的朋友，天体辐射穿过大气到达地面，会产生强度减弱和颜色的变化，也就是大气消光（Atmospheric Extinction）。我们看到星星“眨眼睛”，是因为大气抖动的结果，也属于大气消光。在生活中，我们就可以清楚地体验到大气消光的显著作用：晴天正午的时候，太阳的亮度为-26.7等；早晨或者黄昏，这里是的太阳仅仅有相当于-15.8等的亮度。从天文的角度来讲，大气消光使得太阳亮度减弱了23000倍！

大气消光对天体观测的影响也是非常明显的，在地球上拍摄的天体照片往往比空间望远镜拍摄的模糊。大家比较哈勃空间望远镜与北欧光学望远镜（地面）对木星“写真”就可以发现了。对于我们在观测中获得的天体数据，首先必须经过对大气消光和折光的修正，才能作为下一步使用的数据。

影响因素：

造成大气消光的因素有很多，主要归结为三类：一是大气中各种分子和原子（臭氧和水汽）吸收辐射，使辐射能转变为其他形式的能量，这是一个相对较小的影响，大约把天体的亮度削弱了0.02等。另一个相对大的影响是大气分子的“瑞利散射”现象（Rayleigh scattering），大约把天体亮度降低了0.14等。最后是大气中的悬浮颗粒（尘埃、水滴以及高含量的大气污染物）的散射作用，它把天体亮度降低了0.12等。在标准状况（0℃和标准大气压）下，这三个因素的影响叠加起来，对位于海平面的观测点的总体影响，也就是说平均减弱的星等为0.28。

大气消光与大气的成分、辐射的波长和辐射穿过大气的厚度有关。通常蓝光所受的消光作用比红光严重，辐射穿过大气层的厚度增加，消光作用也加剧。因而主要的因素，当然是天顶角（zenith angle，指星体距离天顶的角度）了。

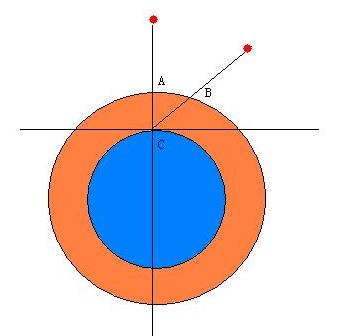
右边的示意图很容易说明为什么天顶角对大气消光有如此显著的影响：天顶来的星光，只需要透过AC一段大气厚度；而非天顶的，则要通过BC一段大气。很明显BC>AC，因而大气的削弱作用也就加强了。

要是把大气层看作是理想的平面，那么很容易就有（z为天顶角）：
$$X \approx \frac{BC}{AC} = \frac{1}{\cos z}$$
然而现实总是不理想的，大气层是环状的，于是我们需要加入修正因子：
$$X = \frac{BC}{AC} = \frac{1}{\cos z + 0.025e^{ - 11\cos z}}$$

此即为天顶距等于z的方向上大气光学厚度和天顶方向大气光学厚度之比，我们把它叫做大气光学质量。其中e是自然对数的底，值为2.71828…，如果把z=45°代进去，可得到BC/AC=1.414…，也就是说在天顶角为45°时，星光需要多通过41.4%的大气。

下图为大气消光随天顶角的变化的曲线图，可以看出，一开始天顶角对大气消光的影响不大，大于75°后急剧上升。

（纵坐标为星等）

我们所看到的星等m'与实际的视星等m的关系为：
$$m' = m + kX$$

这里k为消光因子，是波长的函数，也决定于大气中的物理条件，所以它因时因地而异。近似地有

光的波长 k的值
U（紫外光） 0.6
B（蓝光） 0.4
V（可见光） 0.2
R（红光） 0.1
I（红外光） 0.08

海拔高度也会相应地影响大气折光。我们知道，海拔越高，大气越稀薄，视宁度也越好（也就是看得越清楚）。位于海拔 0.5 km, 1.0 km和2.0 km处，天顶的消光星等分别为0.24, 0.21和0.16。季节也会相应地影响观测，导致消光程度的不同。冬季天空的视宁度比夏季要好，相应地，一天之中视宁度最差的是下午。文章的最后给出了不同季节、海拔和天顶角的消光星等，大家可以作为参考。

大气“透镜”

在初中的物理书我们就可以知道，光线从真空或者一种密度的介质射入到另一种密度的介质时，光线的传播方向会发生改变。同样，大气外的宇宙空间可以近似看作的真空，而当星光通过大气层时，大气层相当于一个透镜，也会使光线发生类似的偏折，这就是大气折光。

大气对蓝光的折射大于对红光的折射，这也是晴天天空呈现蓝色的重要原因。和大气消光一样，大气折光的程度取决于星光需要穿透大气的“大气质量”。有很多公式和计算机程序可以用来修正大气折光。Duffett-Smith提供了几个公式可以精确地计算大气折光率。在天顶角不大于60°，有一个经常用到的简单的估算公式：
$$r \approx k \tan z$$

其中，
r是我们观察到的由于大气折射所增加的高度角
z是天顶角（直角减去高度角）
k取决于光的波长以及观测者的海拔高度。

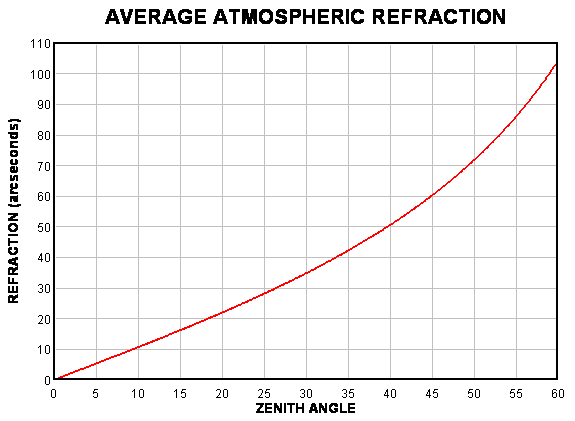
要注意的是实际的高度角等于（我们观测到的高度角－r）。从下图可以看出，在天顶角不大的时候，大气折光的影响相对较小。

（纵坐标为折光角大小，单位为角秒）

在标准大气压下和海平面的情况下，k的平均值为60.3”，而在海拔2km的地方，k的值约为48.8”，大约比海平面减少了19%。换句话说，大气折光率也受到海拔高度的影响。
从波长为400 (蓝光)、500、600到700 (红光)纳米 的光，在标准大气压下对应的k值分别为60.4”、57.8”、57.4” 和57.2”。所以当天顶角增大时，在一个优秀的望远镜中可以看见本来不可见的狭小的红外和蓝外光线谱。举个例子来说，在高度较为30°时，光谱的范围可以达到5.5弧秒。

右图我们很熟悉的太阳和月亮在初升或者将要落下时会发生“变形”，圆形的太阳会变成一个扁平的椭圆，原因之一是大气对光线的偏折，当然其中也包括了大气中灰尘、水蒸汽等紊动对光信号的干扰。要解释这个椭圆的形状，我们必须了解在接近地平线时，大气折射角的增加有多快：
在高度角为2°、1°和0°时，r的值分别为18.4’、24.75’和35.35’。而太阳或者月亮是一个约半度的圆面，圆面上的各点的偏折角都不一样，因而我们看到扁的“太阳”或“月亮”。当太阳出现在地平线的时候，实际它已经在地平线之下了。

话在最后
尽管大气对天文观测造成了不可磨灭的干扰，但是它的伟大作用仍使我们永远不会讨厌它。可以毫不夸张地说，没有大气，就没有生命的存在。作为智慧生物的我们，为了消除大气消光的影响，要做的并不是要“干掉”大气，而是要走出大气的包围。于是，我们便有了各种各样的空间望远镜，如哈勃，以及下一代的韦布！

附1：
不同海拔高度（km）的大气消光表（平均值）

     z     h = 0    h = 0.5    h = 1     h = 2     h = 3
     1      0.28      0.24      0.21      0.16      0.13
    10      0.29      0.24      0.21      0.16      0.13
    20      0.30      0.25      0.22      0.17      0.14
    30      0.32      0.28      0.24      0.19      0.15
    40      0.37      0.31      0.27      0.21      0.17
    45      0.40      0.34      0.29      0.23      0.19
    50      0.44      0.37      0.32      0.25      0.21
    55      0.49      0.42      0.36      0.28      0.23
    60      0.56      0.48      0.41      0.32      0.26
    62      0.60      0.51      0.44      0.34      0.28
    64      0.64      0.54      0.47      0.37      0.30
    66      0.69      0.59      0.51      0.39      0.32
    68      0.75      0.64      0.55      0.43      0.35
    70      0.82      0.70      0.60      0.47      0.39
    71      0.86      0.73      0.63      0.49      0.40
    72      0.91      0.77      0.66      0.52      0.43
    73      0.96      0.81      0.70      0.55      0.45
    74      1.02      0.86      0.74      0.58      0.48
    75      1.08      0.92      0.79      0.62      0.51
    76      1.15      0.98      0.84      0.66      0.54
    77      1.24      1.05      0.91      0.71      0.58
    78      1.34      1.13      0.98      0.76      0.63
    79      1.45      1.23      1.06      0.83      0.68
    80      1.59      1.34      1.16      0.91      0.74
    81      1.75      1.48      1.28      1.00      0.82
    82      1.94      1.65      1.42      1.11      0.91
    83      2.19      1.86      1.60      1.25      1.03
    84      2.50      2.12      1.83      1.43      1.17
    85      2.91      2.46      2.13      1.66      1.36
    86      3.45      2.93      2.53      1.97      1.62
    87      4.23      3.59      3.10      2.42      1.99
    88      5.41      4.59      3.96      3.09      2.54
    89      7.38      6.26      5.40      4.22      3.46
    90     11.24      9.53      8.23      6.42      5.28

不同海拔高度（km）的大气消光表（冬季）

     z     h = 0    h = 0.5    h = 1     h = 2     h = 3
     1      0.25      0.21      0.19      0.15      0.13
    10      0.25      0.22      0.19      0.15      0.13
    20      0.26      0.23      0.20      0.16      0.14
    30      0.28      0.25      0.22      0.17      0.15
    40      0.32      0.28      0.24      0.20      0.17
    45      0.35      0.30      0.26      0.21      0.18
    50      0.38      0.33      0.29      0.24      0.20
    55      0.43      0.37      0.33      0.26      0.22
    60      0.49      0.42      0.37      0.30      0.25
    62      0.52      0.45      0.40      0.32      0.27
    64      0.56      0.48      0.43      0.34      0.29
    66      0.60      0.52      0.46      0.37      0.31
    68      0.65      0.57      0.50      0.40      0.34
    70      0.72      0.62      0.55      0.44      0.37
    71      0.75      0.65      0.57      0.46      0.39
    72      0.79      0.69      0.60      0.49      0.41
    73      0.84      0.72      0.64      0.52      0.43
    74      0.89      0.77      0.68      0.55      0.46
    75      0.94      0.82      0.72      0.58      0.49
    76      1.01      0.87      0.77      0.62      0.52
    77      1.08      0.94      0.82      0.67      0.56
    78      1.16      1.01      0.89      0.72      0.60
    79      1.26      1.10      0.97      0.78      0.66
    80      1.38      1.20      1.06      0.85      0.72
    81      1.52      1.32      1.16      0.94      0.79
    82      1.70      1.47      1.29      1.05      0.88
    83      1.91      1.65      1.46      1.18      0.99
    84      2.18      1.89      1.66      1.34      1.13
    85      2.53      2.20      1.93      1.56      1.31
    86      3.01      2.61      2.30      1.86      1.56
    87      3.69      3.20      2.82      2.28      1.91
    88      4.72      4.09      3.60      2.91      2.45
    89      6.44      5.58      4.91      3.97      3.34
    90      9.80      8.50      7.49      6.05      5.08

不同海拔高度（km）的大气消光表（夏季）

     z     h = 0    h = 0.5    h = 1     h = 2     h = 3
     1      0.32      0.26      0.22      0.17      0.14
    10      0.32      0.27      0.23      0.17      0.14
    20      0.34      0.28      0.24      0.18      0.15
    30      0.37      0.30      0.26      0.20      0.16
    40      0.41      0.34      0.29      0.22      0.18
    45      0.45      0.37      0.32      0.24      0.19
    50      0.49      0.41      0.35      0.26      0.21
    55      0.55      0.46      0.39      0.30      0.24
    60      0.63      0.53      0.45      0.34      0.27
    62      0.68      0.56      0.48      0.36      0.29
    64      0.72      0.60      0.51      0.39      0.31
    66      0.78      0.65      0.55      0.42      0.34
    68      0.85      0.70      0.60      0.45      0.36
    70      0.93      0.77      0.65      0.50      0.40
    71      0.97      0.81      0.69      0.52      0.42
    72      1.02      0.85      0.72      0.55      0.44
    73      1.08      0.90      0.76      0.58      0.47
    74      1.15      0.95      0.81      0.61      0.49
    75      1.22      1.01      0.86      0.65      0.53
    76      1.30      1.08      0.92      0.70      0.56
    77      1.40      1.16      0.99      0.75      0.60
    78      1.51      1.25      1.07      0.81      0.65
    79      1.64      1.36      1.16      0.88      0.71
    80      1.79      1.49      1.26      0.96      0.77
    81      1.97      1.64      1.39      1.06      0.85
    82      2.19      1.83      1.55      1.18      0.95
    83      2.47      2.06      1.75      1.32      1.07
    84      2.82      2.35      1.99      1.51      1.22
    85      3.28      2.73      2.32      1.76      1.41
    86      3.90      3.25      2.75      2.09      1.68
    87      4.78      3.98      3.38      2.56      2.06
    88      6.11      5.09      4.32      3.28      2.63
    89      8.33      6.93      5.89      4.47      3.59
    90     12.68     10.56      8.97      6.80      5.47

附2：
说明：天文奥赛中有一道题目，问晴天和阴天天体的视星等有变化吗？答案是没有的。这里的视星等$m - M = log D - 5$，这里的“视星等”取决于天体的光度和到我们这儿的距离，不受其他外界因素的影响。至于我们看到的变暗、变亮后的星等，不是严格意义上的“视星等”。

附3：
关于“大气光学质量”计算公式，文章里列举的是1966年Rozenberg提出的公式，现在已经衍生出了多的版本，精度各有不同。具体资料可以参考本站链接：http://kexue.fm/archives/396/

文章资料来源：
http://www.asterism.org/tutorials/tut28-1.htm

http://www.cfa.harvard.edu/icq/ICQExtinct.html

转载到请包括本文地址：https://kexue.fm/archives/507

更详细的转载事宜请参考：《科学空间FAQ》