施密特系统的校正镜方程求解

非抛物面望远镜的校正镜方程求解
The Corrector Plate of Non-parabola Telescope

本文在牧夫天文论坛的讨论：
http://www.astronomy.ac/bbs/thread-160257-1-1.html

为了克服折射望远镜的色差问题，1670年，牛顿制造了第一台实用的反射式望远镜，将望远镜的主镜由玻璃透镜换成了抛物反射面，从而消除了色差。然而，相比球面镜，大口径的抛物面并不容易磨制。因为制作大球面镜只需要将曲率相等的小镜片相对自由组合在一起就行了，而抛物线每点的曲率并不相等，所以需要逐个磨制曲率不等的小镜片，并按照严格的顺序组合起来。这无疑大大增加了磨制难度。

为了解决这一难题，天文学家们想到了一个折衷的办法：以球面为主镜，并配以校正镜来校正球差。迎着这一思路，施密特望远镜随之而生。而当代的大望远镜基本上都是沿用这一思路。然而，校正镜是一个比抛物面更加复杂的四次曲面，磨制工艺要求更高，因此，校正镜也不宜过大。

BoJone查阅潘君骅前辈的《光学非球面的设计、加工与检验》后发现，目前求校正镜方程的方法有两种：一是利用所谓“三级象差理论”；二是通过无穷级数来逼近。前者本身就是一种近似理论，结果显然是近似的；后者虽然可以达到任意想要的精度，但是在有限项的情况下以就是近似的。

本文以向量和微积分为基本工具，在已知主镜形状的情况下，求出校正镜（反射镜）的方程。换句话说，就是求出怎样的两块反射镜组合能够将平行射入的光汇集到一点上。我们能够发现，答案有一个简单的形式，而繁琐的地方在于化简的过程。最终得出了施密特望远镜校正境（Schmidt corrector plate）的一般方程，其中包含直角坐标和参数方程两种形式，结果表明这是一条“环面曲线”。

统一方程

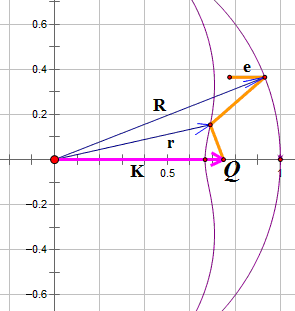
如图所示，主、副境形状分别为$\vec{R},\vec{r}$，光路为$\vec{e} \rightarrow (\vec{r}-\vec{R}) \rightarrow (\vec{K}-\vec{r}) $，Q为焦点，$ \vec{K} $为焦点向量，$ |\vec{e} |=1$。为了表述的方便，令$\vec{D}=\vec{r}-\vec{R} $，记$R,r,D$分别为$\vec{R},\vec{r},\vec{D}$的模。

根据光学的反射定律，$\vec{D}$和$\vec{e}$与$\vec{R}$的切线的夹角相同，因此有
$$\vec{e} \cdot d\vec{R}=\frac{\vec{D}}{D} \cdot d\vec{R}\tag{1}$$
同理
$$ \frac{\vec{D}}{D} \cdot d\vec{r} = \frac{ \vec{K}-\vec{r}}{|\vec{K}-\vec{r} |} \cdot d\vec{r} = -\frac{ \vec{K}-\vec{r}}{|\vec{K}-\vec{r} |} \cdot d(\vec{K}-\vec{r}) $$

利用恒等式$ \vec{r} \cdot d\vec{r} = r dr $得到（对$ \vec{r} ^2= r^2$两边微分立马可以得到这一恒等式）
$$ \frac{\vec{D}}{D} \cdot d\vec{r} = -d|\vec{K}-\vec{r}| \tag{2}$$
(2)-(1)得 $ -d|\vec{K}-\vec{r}|-\vec{e} \cdot d\vec{R} = \frac{\vec{D}}{D} \cdot d(\vec{r}-\vec{R}) = \frac{\vec{D}}{D} \cdot d\vec{D}=dD$

积分一次得
$$ D+|\vec{K}-\vec{r}|+\vec{e} \cdot \vec{R} = C \tag{3}$$另外一道方程由(1)给出，换句话说，(1)和(3)共同确定了$\vec{r}$。这就是非抛物面望远镜的校正镜方程的通用形式。在图中还可以看出焦距$ f=C-R_-$，“$R_-$”是$\vec{R}$在水平位置时的模。当然，实际应用中还需要根据主镜的具体形式，来对校正镜的方程进行化简。下面就针对主镜是球面镜的情况（也就是施密特系统）来体现这一思路。这就是本文的核心内容，去年11月到12月一个多月的思考结果......

施密特系统

建立以圆心为原点的直角坐标系，并进行以下设置：
$$\begin{aligned}\vec{R}=(\cos\theta ,\sin\theta),\dot{\vec{R}}=(-\sin\theta,\cos\theta) \\ \vec{D}=(Dcos\varphi,Dsin\varphi ),\vec{e}=(1,0),\vec{K}=(k,0)\end{aligned}$$
$\vec{r}=(Dcos\varphi+cos\theta,Dsin\varphi+sin\theta )$；初始条件：$\theta=0 \Rightarrow \varphi=\pi$

将其代入(1)，就可以得到
$$\sin\theta=\sin\theta \cos\varphi-\sin\varphi \cos\theta=\sin(\theta-\varphi) \Rightarrow -\pi-\theta=\theta-\varphi$$

那么接着就能够写出
$$\begin{aligned}\cos(\theta-\varphi)=\cos(-\pi-\theta)=-\cos\theta=-\cos(\frac{\varphi-\pi}{2})=-\sin(\frac{\varphi}{2}) \\ \sin\theta=-\cos(\frac{\varphi}{2})\end{aligned}$$

而将其代入(3)，就有
$$\begin{aligned}D+\sqrt{D^2+1+2Dcos(\theta-\varphi)+k^2-2k(Dcos\varphi+\cos\theta)}+\cos\theta =C \\ D+\sqrt{D^2+1-2Dsin\frac{\varphi}{2}+k^2-2k(Dcos\varphi+\sin\frac{\varphi}{2})}+\sin\frac{\varphi}{2}=C \\ D^2+1-2Dsin\frac{\varphi}{2}+k^2-2k[D(1-2\sin^2\frac{\varphi}{2})+\sin\frac{\varphi}{2}]=(C-\sin\frac{\varphi}{2}-D)^2\end{aligned}$$

整理得
$$C^2-1-k^2+(2k-2C) \sin \frac{\varphi}{2} +\sin^2 \frac{\varphi}{2} =4k( \frac{C}{2k}-\frac{1}{2}+ \sin^2\frac{\varphi}{2}-\frac{1}{k} \sin\frac{\varphi}{2})D $$

到了这一步，可以分两种情况讨论：

(1) 当$k = 0$时，
$$C^2-1 + \sin^2 \frac{\varphi}{2} - 2Csin\frac{\varphi}{2} =4(- \sin \frac{\varphi}{2} +\frac{C}{2})D$$

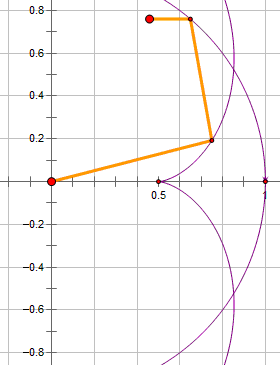
为了使形式更加简单，我们取C=2，得到$4D=3-sin\frac{\varphi}{2}$；如果将这个结果代入$\vec{r}=(Dcos\varphi+ sin\frac{\varphi}{2},Dsin\varphi - cos\frac{\varphi}{2} )$，并换回直角坐标系，不难发现这个一个六次函数。用它所构成的望远镜如图：

(2) 当$k != 0$时，我们不妨想办法将D变成一个常数，也就是要求
$$\begin{aligned}C^2-1-k^2=\frac{C}{2k}-\frac{1}{2} \\ C-k=\frac{1}{2k}\end{aligned}$$
（这样两端才能通约）

令人惊喜的是上面两式居然是自洽的，也就是
$$C^2-1-k^2=\frac{C}{2k}-\frac{1}{2} \Leftrightarrow C-k=\frac{1}{2k}$$

那么就有$D=\frac{1}{4k}$，这就是我们所希望的结果！因为这样既把方程形式变成最简，而结果又是不唯一的（k可以自由设置）

根据$\vec{r}=(Dcos\varphi+ sin\frac{\varphi}{2},Dsin\varphi - cos\frac{\varphi}{2} )$，
令$x=Dcos\varphi+ sin\frac{\varphi}{2} ,y=Dsin\varphi - cos\frac{\varphi}{2}$
有$x^2+y^2=D^2+1-2Dsin\frac{\varphi}{2}$

$$x=D(1-2\sin^2 \frac{\varphi}{2})+ \sin\frac{\varphi}{2} =D[1-2(\frac{D^2+1-x^2-y^2}{2D})^2]+(\frac{D^2+1-x^2-y^2}{2D})$$

展开之后就是
$$( x^2+y^2)^2-(1+\frac{1}{8k^2}) (x^2+y^2)+( \frac{1}{256 k^4}-\frac{1}{16 k^2} ) + \frac{x}{2k}=0$$

这是一个四次函数（利用数学软件可以快速地展开成$ x = f(y^2) $的级数形式），这种形式的曲线也叫“环面曲线”（toric section，正如圆锥曲线是圆锥面和平面相交而成的，它是由平面和环面相交形成的曲线）。它的焦距为$f=C-1=\frac{1}{2k}+k-1$。

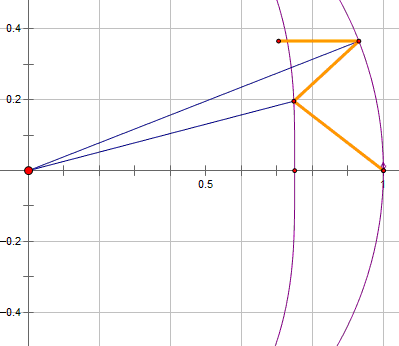
当$k=1$时结构如下：

这就是我们最常见的施密特系统的光学结构，校正板方程为
$$(x^2+y^2)^2-\frac{9 }{8}(x^2+y^2)+\frac{x}{2}-\frac{15}{256}=0$$

不难发现，校正板中心部分是很接近直线的。这表明当球面不大时，是可以将其当成焦距为半径一半的抛物面来使用。事实上，当x=0.7499999，y=0.015，也就是说，精度为0.0000001时，口径（直径）为0.06、球半径为1的球面镜可以当作一个焦距为0.5的抛物面镜来使用的。

分析总结

本文使用向量和基本微积分为工具，先得出了“非抛物面望远镜的校正镜方程的通用形式”，然后以此为基础，对施密特系统进行了简要分析，最后得出了施密特系统的校正板的方程以及焦距公式等结果。BoJone是一个天文爱好者，更是一个数学爱好者。在写这篇文章时，并没有阅读现行的一些光学著作，因此在表达和记号方面可能会与这些著作有些出入。笔者纯粹是将其当作一个普通的物理数学问题进行分析，得出一点小小的结果，遂与大家分享，希冀能够起到抛砖引玉的效果。

参考：
1、潘君骅前辈的《光学非球面的设计、加工与检验》
2、维基百科“环面曲线”：
http://zh.wikipedia.org/zh-cn/%E7%92%B0%E9%9D%A2%E6%9B%B2%E7%B7%9A

3、向量应用：
http://kexue.fm/search/%E5%90%91%E9%87%8F/

转载到请包括本文地址：https://kexue.fm/archives/1257

更详细的转载事宜请参考：《科学空间FAQ》