三个相切圆的公切圆:补充
By 苏剑林 | 2014-01-30 | 24833位读者 | 引用在学车的时候,我堂大哥曾问我一道作圆的问题:
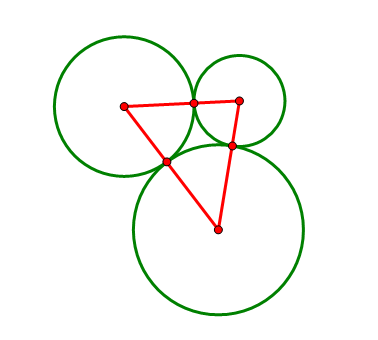
平面上给出三个两两相切的圆以及它们的圆心,求作一个圆与这三个圆都相切(尺规作图)。
如果从纯几何的途径入手,我们甚至很难判断这样的圆是否存在。但是我之前似乎已经看过类似的题目,于是很快想到一个名词:反演。反演可以将圆反演成直线(圆过反演点),也可以将圆反演成圆(圆不过反演点),而其他的相切、相交等关系保持不变。对反演后的图形进行相同的反演,就变回原来的图形。本题的难点在于圆太多,利用反演,我们可以将它变为两条直线和一个圆的问题。
假设读者已经有了反演的基本知识,如果没有,请到
http://zh.wikipedia.org/wiki/反演
阅读相关内容。
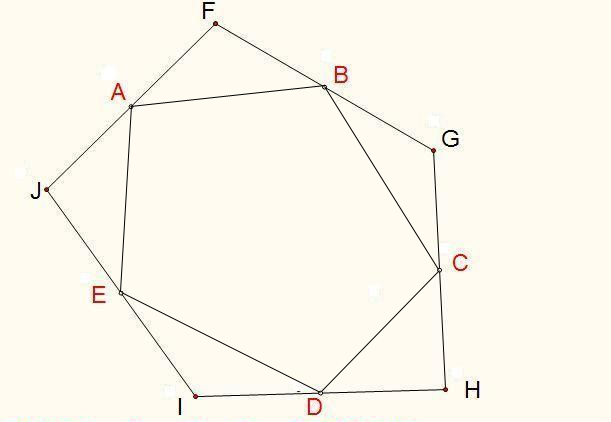
已知中心五边形,作五边形
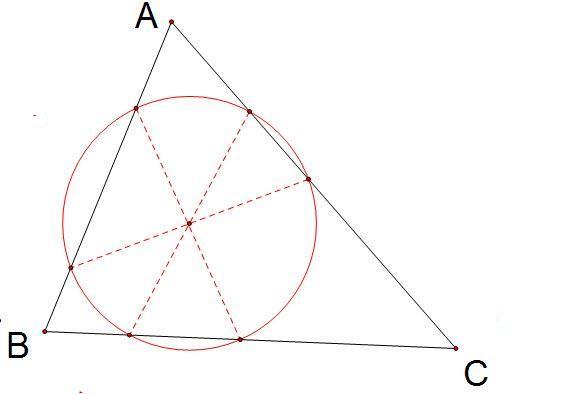
By 苏剑林 | 2010-07-25 | 29691位读者 | 引用神秘的圆——三角形的“六接圆”(添加新方法)
By 苏剑林 | 2010-07-24 | 28478位读者 | 引用正十七边形的尺规作图存在之证明
By 苏剑林 | 2009-09-20 | 45975位读者 | 引用正十七边形的尺规作图
By 苏剑林 | 2009-08-28 | 35830位读者 | 引用为何正17边形能够用尺规作出来?要如何作?先别急,请看下面的解释:
一个正质数多边形可以用标尺作图的充分和必要条件是,该多边形的边数必定是一个费马质数。换句话说,只有正三边形、正五边形、正十七边形、正257边形和正63357边形可以用尺规作出来,其它的正质数多边形就不可以了。(除非我们再发现另一个费马质数。)
正17边形的尺规作法是高斯在1796年得出的,他也因此决心要成为数学家。关于费马质数,是指形如$2^{2^n}+1$的质数,一开始费马认为对于所有的n,这种形式的数都是质数。可是这似乎是上天的玩笑,目前只发现了当n=0,1,2,3,4的时候$2^{2^n}+1$是质数,其余都是合数。








最近评论