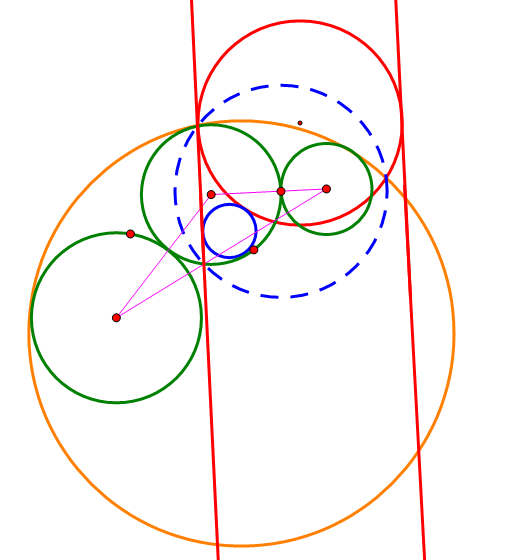
文章《三个相切圆的公切圆》中，笔者讲到利用反演作三个相切圆的公切圆，那时要求三个圆要两两相切。后来思考了一下，发现不用这个条件，只要三个之中的一个圆与另外两个圆都相切即可。

甚至，可以更宽松，三个圆之中，两个圆相切，第三个圆不一定相切的情况下都可以存在满足条件的公切圆。至于第三个圆的充分必要条件，则可以从它的反演像中可以看出：第三个圆的反演像要跟两条平行线之间的区域有交集。

三个圆的公切圆1

三个圆的公切圆1

三个圆的公切圆2

三个圆的公切圆2

转载到请包括本文地址：https://kexue.fm/archives/2333

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jan. 30, 2014). 《三个相切圆的公切圆:补充 》[Blog post]. Retrieved from https://kexue.fm/archives/2333

@online{kexuefm-2333,
        title={三个相切圆的公切圆:补充},
        author={苏剑林},
        year={2014},
        month={Jan},
        url={\url{https://kexue.fm/archives/2333}},
}