WGAN的成功，可能跟Wasserstein距离没啥关系

WGAN，即Wasserstein GAN，算是GAN史上一个比较重要的理论突破结果，它将GAN中两个概率分布的度量从f散度改为了Wasserstein距离，从而使得WGAN的训练过程更加稳定，而且生成质量通常也更好。Wasserstein距离跟最优传输相关，属于Integral Probability Metric（IPM）的一种，这类概率度量通常有着更优良的理论性质，因此WGAN的出现也吸引了很多人从最优传输和IPMs的角度来理解和研究GAN模型。

然而，最近Arxiv上的论文《Wasserstein GANs Work Because They Fail (to Approximate the Wasserstein Distance)》则指出，尽管WGAN是从Wasserstein GAN推导出来的，但是现在成功的WGAN并没有很好地近似Wasserstein距离，相反如果我们对Wasserstein距离做更好的近似，效果反而会变差。事实上，笔者一直以来也有这个疑惑，即Wasserstein距离本身并没有体现出它能提升GAN效果的必然性，该论文的结论则肯定了该疑惑，所以GAN能成功的原因依然很迷～

基础与回顾 #

本文是对WGAN训练过程的探讨，并不算入门文章。关于初学GAN，欢迎参考《互怼的艺术：从零直达WGAN-GP》；而关于f散度与GAN之间的联系，可以参考《f-GAN简介：GAN模型的生产车间》和《Designing GANs：又一个GAN生产车间》；至于WGAN的理论推导，可以参考《从Wasserstein距离、对偶理论到WGAN》；对于GAN的训练过程分析，还可以参考《从动力学角度看优化算法（四）：GAN的第三个阶段》。

一般来说，GAN对应着一个min-max过程：
\begin{equation}\min_G \max_D \mathcal{L}(D, G)\end{equation}
当然，一般来说判别器和生成器的损失函数可能不一样，但上述形式已经足够有代表性了。最原始的GAN一般称为vanilla GAN，其形式为
\begin{equation}\min_G \max_D \mathbb{E}_{x\sim p(x)}\left[\log D(x)\right] + \mathbb{E}_{z\sim q(z)}\left[\log (1 - D(G(z)))\right]\label{eq:v-gan}\end{equation}
可以参考《Towards Principled Methods for Training Generative Adversarial Networks》、《令人拍案叫绝的Wasserstein GAN》或本博客GAN相关的文章证明，vanilla GAN实际上相对于在缩小两个分布之间的JS散度。而JS散度是f散度的一种，所有的f散度都具有一个问题，那就是在两个分布几乎没有交集的时候，散度为一个常数，这意味着梯度为零，而我们是使用梯度下降求解的，所以这意味着我们无法很好地完成优化。为此，WGAN应运而生，它利用Wasserstein距离来设计了新的GAN：
\begin{equation}\min_G \max_{\Vert D\Vert_{L}\leq 1} \mathbb{E}_{x\sim p(x)}\left[D(x)\right] - \mathbb{E}_{z\sim q(z)}\left[D(G(z))\right]\label{eq:w-gan}\end{equation}
跟之前的GAN的明显区别是，WGAN显式地给判别器$D$加上了L约束$\Vert D\Vert_{L}\leq 1$。由于Wasserstein距离几乎对任意两个分布（哪怕没有交集）都有比较良好的定义，因此WGAN理论上就解决了传统的基于f散度的GAN的梯度消失、训练不稳定等问题。

给判别器加上L约束主要有两个主要方案：一是谱归一化（Spectral Normalization，SN），可以参考《深度学习中的Lipschitz约束：泛化与生成模型》，现在很多GAN（不限于WGAN）为了稳定训练，都往判别器甚至生成器上都加入谱归一化了；二是梯度惩罚（Gradient Penalty，GP），其中有包括以1为中心的惩罚（WGAN-GP）和以0为中心的惩罚（WGAN-div）两种，可以参考《WGAN-div：一个默默无闻的WGAN填坑者》，目前的结果表明零中心惩罚具有比较好的理论性质和效果。

效果 ≠ 近似 #

事实上“WGAN并没有很好近似Wasserstein距离”这个现象也不是第一次被关注了，比如2019年就有论文《How Well Do WGANs Estimate the Wasserstein Metric?》系统地讨论过这一点。而本文要介绍的论文，则通过比较严谨地设置实验来确定WGAN效果的好坏与Wasserstein距离近似程度的联系。

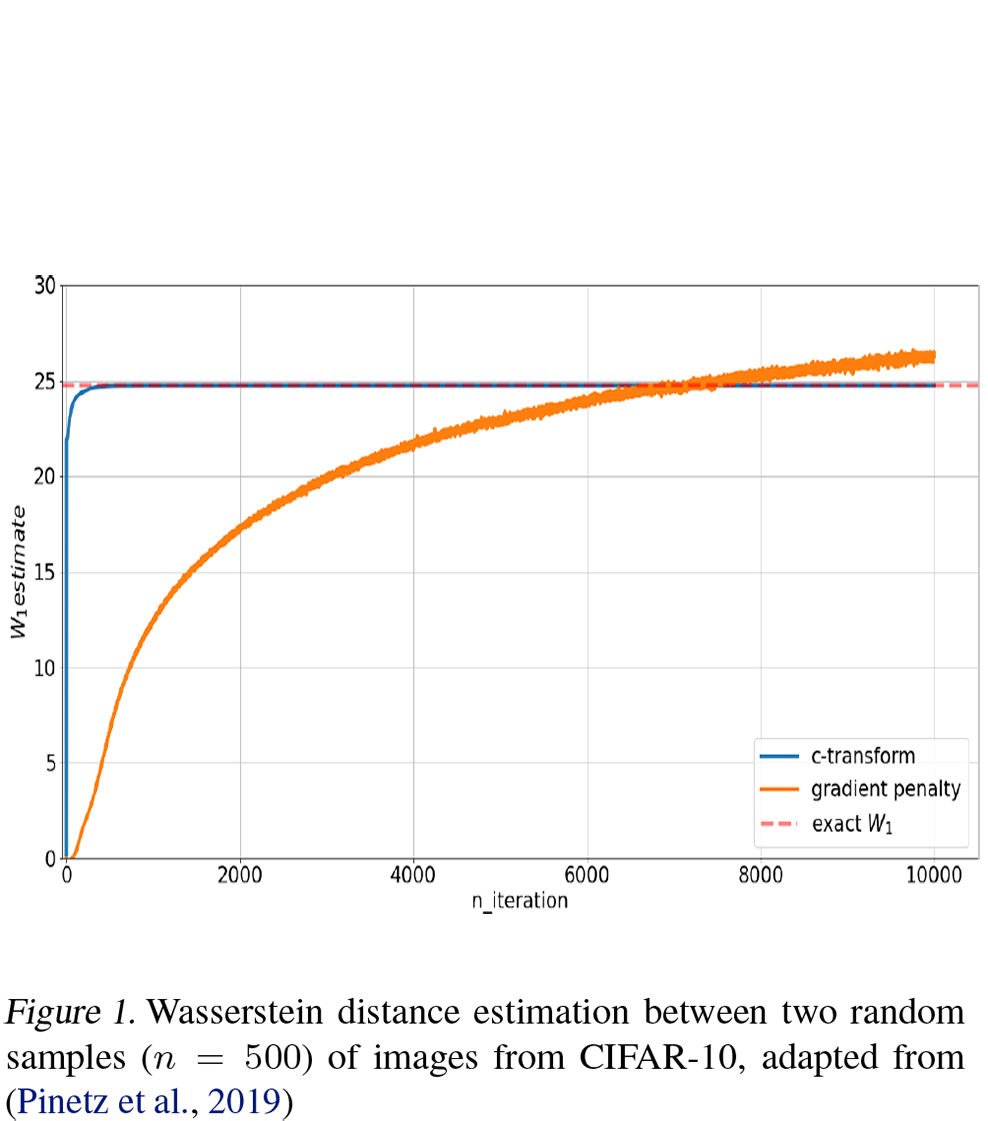
首先，论文比较了梯度惩罚（GP）与一种称为$c\text{-transform}$的方法在实现WGAN时的效果。$c\text{-transform}$同样提出自论文《How Well Do WGANs Estimate the Wasserstein Metric?》，它相比梯度惩罚能更好地近似Wasserstein距离。下面两个图也表明了这一点：

然而，$c\text{-transform}$的生成效果，却并不如梯度惩罚：

当然，原论文选这个图真是让人哭笑不得，事实上WGAN-GP的效果可以比上面右图好得多。于是，我们可以暂时下结论：

1、效果好的WGAN在训练过程中并没有很好地近似Wasserstein距离；

2、更好地近似Wasserstein距离究竟对提升生成效果并没有帮助。

理论 ≠ 实验 #

现在就让我们来思考一下问题出在哪。我们知道，不管是原始GAN$\eqref{eq:v-gan}$还是WGAN$\eqref{eq:w-gan}$又或者其他GAN，在实验的时候，都有两个共同特点：

1、$\min$和$\max$是交替训练的；

2、每次都只是随机选一个batch来训练。

这两点有什么问题呢？

第一，其实几乎所有的GAN都会写成$\min\limits_G \max\limits_D$，这是因为理论上来说，需要先精确完成$\max\limits_D$，然后再去$\min\limits_G$，才是在优化GAN对应的概率度量，如果只是交替优化，那么理论上就不可能很精确地逼近概率度量。哪怕WGAN因为用了Wasserstein距离不怕消失，所以交替训练时通常会多训练几步$D$（或者$D$用更大的学习率），但依旧不可能精确逼近Wasserstein距离，这是差距来源之一。

第二，随机采样一个batch来训练，而不是全量训练样本，这导致的一个结果是“训练集里边随机选两个batch的Wasserstein距离，还大于训练集的batch与其平均样本之间的Wasserstein距离”，如下图所示：

这就说明了，基于batch训练的情况下，如果你希望得到更真实的样本，那么必然不是在优化Wasserstein距离，如果你在很精确地优化Wasserstein距离，那么就得不到更真实的样本，因为模糊的平均样本的Wasserstein距离还更小。

数学 ≠ 视觉 #

从数学上来看，Wasserstein距离的性质确实是非常漂亮的，某种意义上来说它是度量任意两个分布之间差距的最佳方案。但是数学归数学，Wasserstein距离最“致命”的地方在于它是依赖于具体的度量的：
\begin{equation}\mathcal{W}[p,q]=\inf_{\gamma\in \Pi[p,q]} \iint \gamma(x,y) d(x,y) dxdy\end{equation}
也就是说，我们需要给定一个能度量两个样本差距的函数$d(x,y)$。然而，对于很多场景，比如两张图片，度量函数的设计本身就是难中之难。WGAN直接使用了欧氏距离$d(x,y)=\Vert x - y\Vert_2$，尽管在数学上是合理的，但在视觉效果上却是不合理的，我们肉眼认为的两张更相似的图片，它的欧氏距离未必更小。所以如果很精确地去近似Wasserstein距离，反而会带来视觉效果上的变差。原论文也做了实验，通过$c\text{-transform}$对Wasserstein距离做更好的近似，那么模型的生成效果其实跟K-Means聚类中心是类似的，而K-Means也正是使用了欧式距离作为度量：

所以，现在WGAN成功的原因就很迷了：WGAN是基于Wasserstein距离推导出来的，然后在实现上却跟Wasserstein距离有点差距，而这个差距很可能才是WGAN成功的关键。原论文认为WGAN的最关键之处是引入了L约束，往任意一个GAN变种里边引入L约束（谱归一化或梯度惩罚），多多少少都能使得效果和稳定性有点提升，因此L约束才是提升的要点，而并不是想象中的Wasserstein距离。

但这更多的只是一个结论，还不是理论上的分析。看来对GAN的深入理解，还是任重而道远啊～

简单的总结 #

本文主要分享了最近的一篇论文，里边指出对Wasserstein距离的近似与否，跟WGAN的效果好坏并没有必然联系，如何更好地理解GAN的理论与实践，依然是一种艰难的任务～

转载到请包括本文地址：https://kexue.fm/archives/8244

更详细的转载事宜请参考：《科学空间FAQ》