Transformer升级之路:1、Sinusoidal位置编码追根溯源
By 苏剑林 | 2021-03-08 | 252710位读者 |最近笔者做了一些理解和改进Transformer的尝试,得到了一些似乎还有价值的经验和结论,遂开一个专题总结一下,命名为“Transformer升级之路”,既代表理解上的深入,也代表结果上的改进。
作为该专题的第一篇文章,笔者将会介绍自己对Google在《Attention is All You Need》中提出来的Sinusoidal位置编码
\begin{equation}\left\{\begin{aligned}&\boldsymbol{p}_{k,2i}=\sin\Big(k/10000^{2i/d}\Big)\\
&\boldsymbol{p}_{k, 2i+1}=\cos\Big(k/10000^{2i/d}\Big)
\end{aligned}\right.\label{eq:sin}\end{equation}
的新理解,其中$\boldsymbol{p}_{k,2i},\boldsymbol{p}_{k,2i+1}$分别是位置$k$的编码向量的第$2i,2i+1$个分量,$d$是向量维度。
作为位置编码的一个显式解,Google在原论文中对它的描述却寥寥无几,只是简单提及了它可以表达相对位置信息,后来知乎等平台上也出现了一些解读,它的一些特点也逐步为大家所知,但总体而言比较零散。特别是对于“它是怎么想出来的”、“非得要这个形式不可吗”等原理性问题,还没有比较好的答案。
因此,本文主要围绕这些问题展开思考,可能在思考过程中读者会有跟笔者一样的感觉,即越思考越觉得这个设计之精妙漂亮,让人叹服~
泰勒展开 #
假设我们的模型为$f(\cdots,\boldsymbol{x}_m,\cdots,\boldsymbol{x}_n,\cdots)$,其中标记出来的$\boldsymbol{x}_m,\boldsymbol{x}_n$分别表示第$m,n$个输入,不失一般性,设$f$是标量函数。对于不带Attention Mask的纯Attention模型,它是全对称的,即对于任意的$m,n$,都有
\begin{equation}f(\cdots,\boldsymbol{x}_m,\cdots,\boldsymbol{x}_n,\cdots)=f(\cdots,\boldsymbol{x}_n,\cdots,\boldsymbol{x}_m,\cdots)\end{equation}
这就是我们说Transformer无法识别位置的原因——全对称性,简单来说就是函数天然满足恒等式$f(x,y)=f(y,x)$,以至于我们无法从结果上区分输入是$[x,y]$还是$[y,x]$。
因此,我们要做的事情,就是要打破这种对称性,比如在每个位置上都加上一个不同的编码向量:
\begin{equation}\tilde{f}(\cdots,\boldsymbol{x}_m,\cdots,\boldsymbol{x}_n,\cdots)=f(\cdots,\boldsymbol{x}_m + \boldsymbol{p}_m,\cdots,\boldsymbol{x}_n + \boldsymbol{p}_n,\cdots)\end{equation}
一般来说,只要每个位置的编码向量不同,那么这种全对称性就被打破了,即可以用$\tilde{f}$代替$f$来处理有序的输入。但现在我们希望能进一步分析位置编码的性质,甚至得到一个显式解,那么就不能止步于此。
为了简化问题,我们先只考虑$m,n$这两个位置上的位置编码,将它视为扰动项,泰勒展开到二阶:
\begin{equation}\tilde{f}\approx f + \boldsymbol{p}_m^{\top} \frac{\partial f}{\partial \boldsymbol{x}_m} + \boldsymbol{p}_n^{\top} \frac{\partial f}{\partial \boldsymbol{x}_n} + \frac{1}{2}\boldsymbol{p}_m^{\top} \frac{\partial^2 f}{\partial \boldsymbol{x}_m^2}\boldsymbol{p}_m + \frac{1}{2}\boldsymbol{p}_n^{\top} \frac{\partial^2 f}{\partial \boldsymbol{x}_n^2}\boldsymbol{p}_n + \underbrace{\boldsymbol{p}_m^{\top} \frac{\partial^2 f}{\partial \boldsymbol{x}_m \partial \boldsymbol{x}_n}\boldsymbol{p}_n}_{\boldsymbol{p}_m^{\top} \boldsymbol{\mathcal{H}} \boldsymbol{p}_n}\end{equation}
可以看到,第1项跟位置无关,第2到5项都只依赖于单一位置,所以它们是纯粹的绝对位置信息,第6项是第一个同时包含$\boldsymbol{p}_m,\boldsymbol{p}_n$的交互项,我们将它记为$\boldsymbol{p}_m^{\top} \boldsymbol{\mathcal{H}} \boldsymbol{p}_n$,希望它能表达一定的相对位置信息。
(此处的泰勒展开参考了知乎问题《BERT为何使用学习的position embedding而非正弦position encoding?》上的纳米酱的回复。)
相对位置 #
我们先从简单的例子入手,假设$\boldsymbol{\mathcal{H}}=\boldsymbol{I}$是单位矩阵,此时$\boldsymbol{p}_m^{\top} \boldsymbol{\mathcal{H}} \boldsymbol{p}_n = \boldsymbol{p}_m^{\top} \boldsymbol{p}_n = \langle\boldsymbol{p}_m, \boldsymbol{p}_n\rangle$是两个位置编码的内积,我们希望在这个简单的例子中该项表达的是相对位置信息,即存在某个函数$g$使得
\begin{equation}\langle\boldsymbol{p}_m, \boldsymbol{p}_n\rangle = g(m-n)\label{eq:r1}\end{equation}
这里的$\boldsymbol{p}_m, \boldsymbol{p}_n$是$d$维向量,这里我们从最简单$d=2$入手。
对于2维向量,我们借助复数来推导,即将向量$[x,y]$视为复数$x + y\text{i}$,根据复数乘法的运算法则,我们不难得到:
\begin{equation}\langle\boldsymbol{p}_m, \boldsymbol{p}_n\rangle = \text{Re}[\boldsymbol{p}_m \boldsymbol{p}_n^*]\end{equation}
其中$\boldsymbol{p}_n^*$是$\boldsymbol{p}_n$的共轭复数,$\text{Re}[]$代表复数的实部。为了满足式$\eqref{eq:r1}$,我们可以假设存在复数$\boldsymbol{q}_{m-n}$使得
\begin{equation}\boldsymbol{p}_m \boldsymbol{p}_n^* = \boldsymbol{q}_{m-n}\end{equation}
这样两边取实部就得到了式$\eqref{eq:r1}$。为了求解这个方程,我们可以使用复数的指数形式,即设$\boldsymbol{p}_m=r_m e^{\text{i}\phi_m}, \boldsymbol{p}_n^*=r_n e^{-\text{i}\phi_n}, \boldsymbol{q}_{m-n}=R_{m-n} e^{\text{i}\Phi_{m-n}}$得到
\begin{equation}r_m r_n e^{\text{i}(\phi_m - \phi_n)} = R_{m-n} e^{\text{i}\Phi_{m-n}}\quad\Rightarrow\quad \left\{\begin{aligned}&r_m r_n = R_{m-n}\\ & \phi_m - \phi_n=\Phi_{m-n}\end{aligned}\right.\end{equation}
对于第一个方程,代入$n=m$得$r_m^2=R_0$,即$r_m$是一个常数,简单起见这里设为1就好;对于第二个方程,代入$n=0$得$\phi_m - \phi_0=\Phi_m$,简单起见设$\phi_0=0$,那么$\phi_m=\Phi_m$,即$\phi_m - \phi_n=\phi_{m-n}$,代入$n=m-1$得$\phi_m - \phi_{m-1}=\phi_1$,那么$\{\phi_m\}$只是一个等差数列,通解为$m\theta$,因此我们就得到二维情形下位置编码的解为:
\begin{equation}\boldsymbol{p}_m = e^{\text{i}m\theta}\quad\Leftrightarrow\quad \boldsymbol{p}_m=\begin{pmatrix}\cos m\theta \\ \sin m\theta\end{pmatrix}\end{equation}
由于内积满足线性叠加性,所以更高维的偶数维位置编码,我们可以表示为多个二维位置编码的组合:
\begin{equation}\boldsymbol{p}_m = \begin{pmatrix}e^{\text{i}m\theta_0} \\ e^{\text{i}m\theta_1} \\ \vdots \\ e^{\text{i}m\theta_{d/2-1}}\end{pmatrix}\quad\Leftrightarrow\quad \boldsymbol{p}_m=\begin{pmatrix}\cos m\theta_0 \\ \sin m\theta_0 \\ \cos m\theta_1 \\ \sin m\theta_1 \\ \vdots \\ \cos m\theta_{d/2-1} \\ \sin m\theta_{d/2-1} \end{pmatrix}\label{eq:r2}\end{equation}
它同样满足式$\eqref{eq:r1}$。当然,这只能说是式$\eqref{eq:r1}$的一个解,但不是唯一解,对于我们来说,求出一个简单的解就行了。
远程衰减 #
基于前面的假设,我们推导出了位置编码的形式$\eqref{eq:r2}$,它跟标准的Sinusoidal位置编码$\eqref{eq:sin}$形式基本一样了,只是$\sin,\cos$的位置有点不同。一般情况下,神经网络的神经元都是无序的,所以哪怕打乱各个维度,也是一种合理的位置编码,因此除了各个$\theta_i$没确定下来外,式$\eqref{eq:r2}$和式$\eqref{eq:sin}$并无本质区别。
式$\eqref{eq:sin}$的选择是$\theta_i = 10000^{-2i/d}$,这个选择有什么意义呢?事实上,这个形式有一个良好的性质:它使得随着$|m-n|$的增大,$\langle\boldsymbol{p}_m, \boldsymbol{p}_n\rangle$有着趋于零的趋势。按照我们的直观想象,相对距离越大的输入,其相关性应该越弱,因此这个性质是符合我们的直觉的。只是,明明是周期性的三角函数,怎么会呈现出衰减趋势呢?
这的确是个神奇的现象,源于高频振荡积分的渐近趋零性。具体来说,我们将内积写为
\begin{equation}\begin{aligned}
\langle\boldsymbol{p}_m, \boldsymbol{p}_n\rangle =&\, \text{Re}\left[e^{\text{i}(m-n)\theta_0} + e^{\text{i}(m-n)\theta_1} + \cdots + e^{\text{i}(m-n)\theta_{d/2-1}}\right]\\
=&\,\frac{d}{2}\cdot\text{Re}\left[\sum_{i=0}^{d/2-1} e^{\text{i}(m-n)10000^{-i/(d/2)}}\frac{1}{d/2}\right]\\
\sim&\, \frac{d}{2}\cdot\text{Re}\left[\int_0^1 e^{\text{i}(m-n)\cdot 10000^{-t}}dt\right]
\end{aligned}\end{equation}
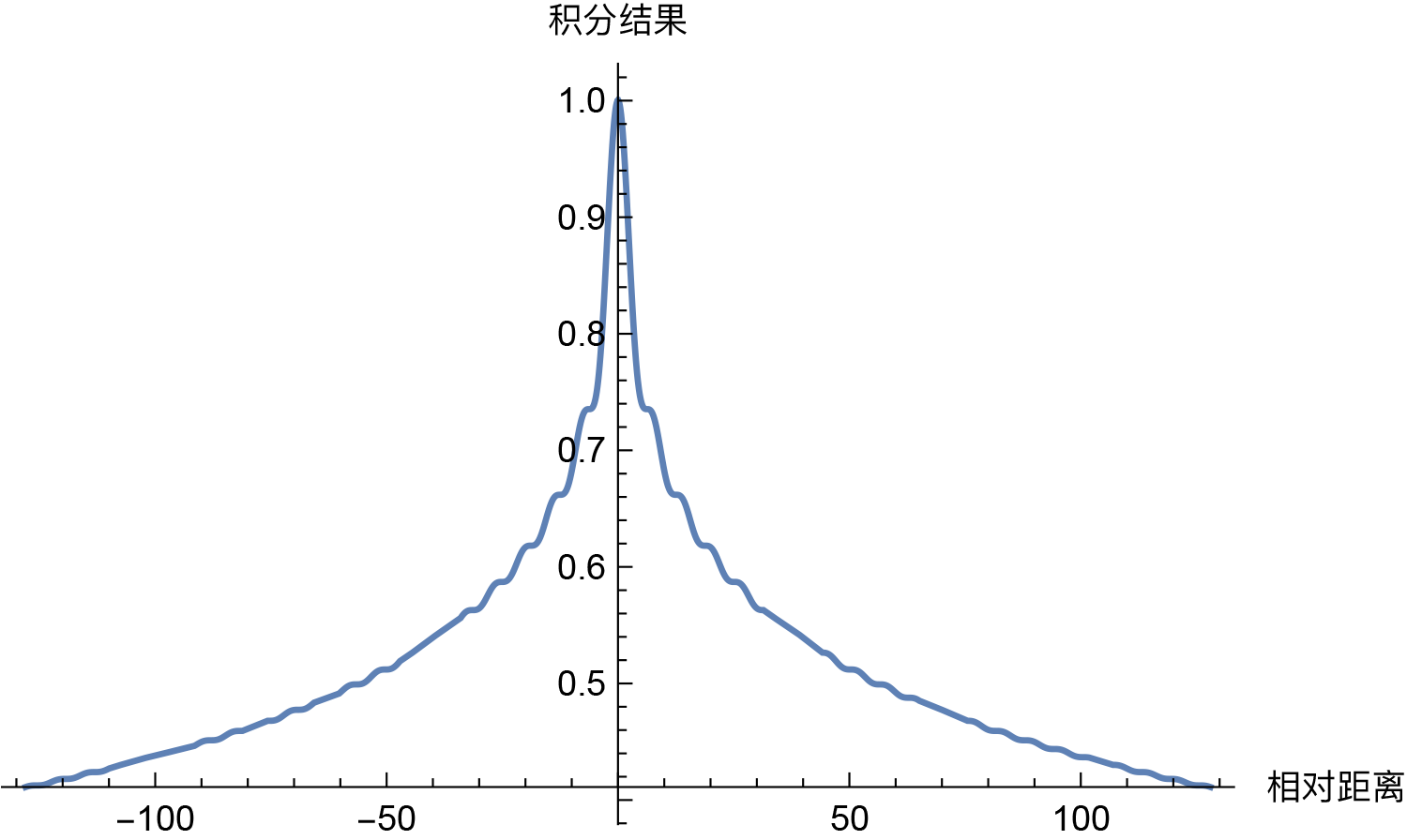
这样问题就变成了积分$\int_0^1 e^{\text{i}(m-n)\theta_t}dt$的渐近估计问题了。其实这种振荡积分的估计在量子力学中很常见,可以利用其中的方法进行分析,但对于我们来说,最直接的方法就是通过Mathematica把积分结果的图像画出来:
\[Theta][t_] = (1/10000)^t;
f[x_] = Re[Integrate[Exp[I*x*\[Theta][t]], {t, 0, 1}]];
Plot[f[x], {x, -128, 128}]然后从图像中我们就可以看出确实具有衰减趋势:
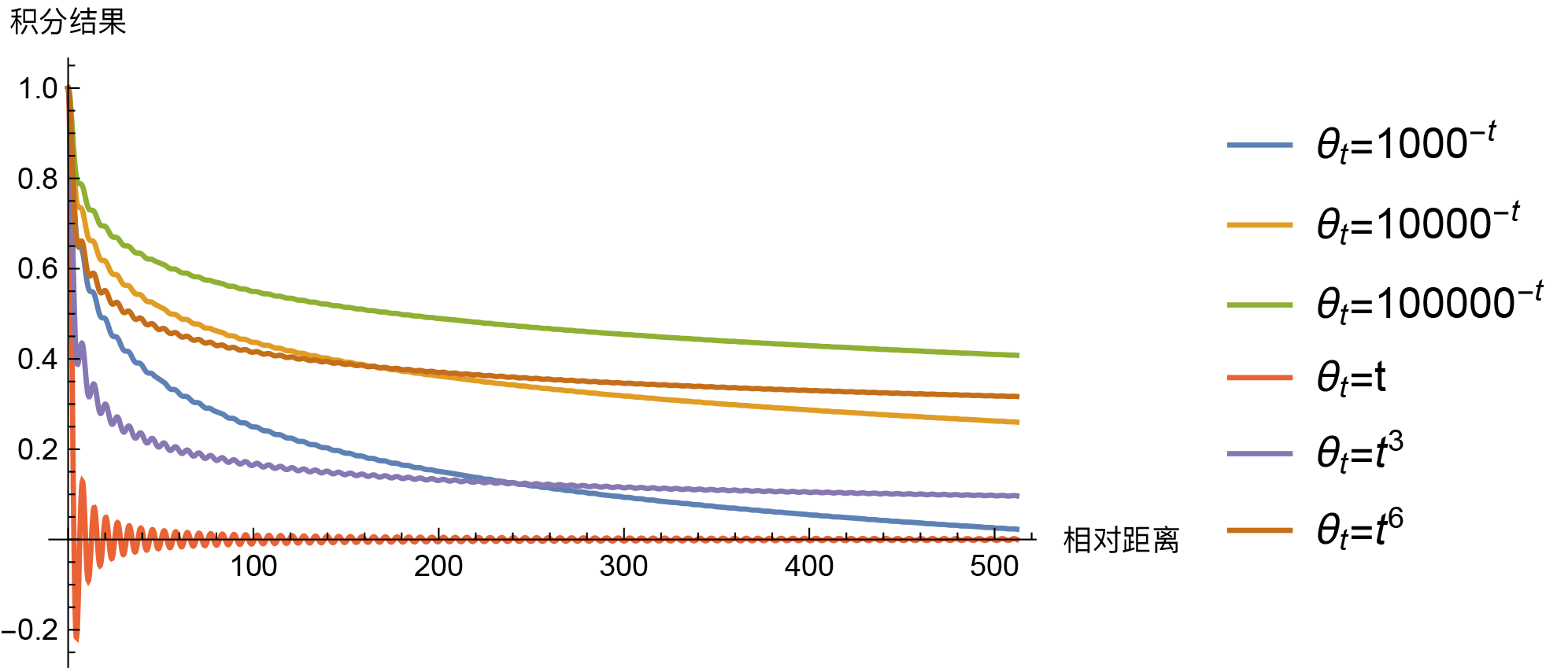
那么,问题来了,必须是$\theta_t = 10000^{-t}$才能呈现出远程衰减趋势吗?当然不是。事实上,对于我们这里的场景,“几乎”每个$[0,1]$上的单调光滑函数$\theta_t$,都能使得积分$\int_0^1 e^{\text{i}(m-n)\theta_t}dt$具有渐近衰减趋势,比如幂函数$\theta_t = t^{\alpha}$。那么,$\theta_t = 10000^{-t}$有什么特别的吗?我们来比较一些结果。
就这样看上去,除了$\theta_t=t$比较异常之外(与横轴有交点),其他都没有什么明显的区分度,很难断定孰优孰劣,无非就是幂函数在短距离降得快一点,而指数函数则在长距离降得快一点,$\theta_t$整体越接近于0,那么整体就降得慢一些,等等。如此看来$\theta_t = 10000^{-t}$也只是一个折中的选择,没有什么特殊性,要是笔者来选,多半会选$\theta_t = 1000^{-t}$。还有一个方案是,直接让$\theta_i = 10000^{-2i/d}$作为各个$\theta_i$的初始化值,然后将它设为可训练的,由模型自动完成微调,这样也不用纠结选哪个了。
一般情况 #
前面两节中,我们展示了通过绝对位置编码来表达相对位置信息的思想,加上远程衰减的约束,可以“反推”出Sinusoidal位置编码,并且给出了关于$\theta_i$的其他选择。但是别忘了,到目前为止,我们的推导都是基于$\boldsymbol{\mathcal{H}}=\boldsymbol{I}$这个简单情况的,对于一般的$\boldsymbol{\mathcal{H}}$,使用上述Sinusoidal位置编码,还能具备以上的良好性质吗?
如果$\boldsymbol{\mathcal{H}}$是一个对角阵,那么上面的各个性质可以得到一定的保留,此时
\begin{equation}\boldsymbol{p}_m^{\top} \boldsymbol{\mathcal{H}} \boldsymbol{p}_n=\sum_{i=1}^{d/2} \boldsymbol{\mathcal{H}}_{2i,2i} \cos m\theta_i \cos n\theta_i + \boldsymbol{\mathcal{H}}_{2i+1,2i+1} \sin m\theta_i \sin n\theta_i\end{equation}
由积化和差公式得到
\begin{equation}\sum_{i=1}^{d/2} \frac{1}{2}\left(\boldsymbol{\mathcal{H}}_{2i,2i} + \boldsymbol{\mathcal{H}}_{2i+1,2i+1}\right) \cos (m-n)\theta_i + \frac{1}{2}\left(\boldsymbol{\mathcal{H}}_{2i,2i} - \boldsymbol{\mathcal{H}}_{2i+1,2i+1}\right) \cos (m+n)\theta_i \end{equation}
可以看到它也是确实包含了相对位置$m-n$,只不过可能会多出$m+n$这一项,如果不需要它,模型可以让$\boldsymbol{\mathcal{H}}_{2i,2i} = \boldsymbol{\mathcal{H}}_{2i+1,2i+1}$来消除它。在这个特例下,我们指出的是Sinusoidal位置编码赋予了模型学习相对位置的可能,至于具体需要什么位置信息,则由模型的训练自行决定。
特别地,对于上式,远程衰减特性依然存在,比如第一项求和,类比前一节的近似,它相当于积分
\begin{equation}\sum_{i=1}^{d/2} \frac{1}{2}\left(\boldsymbol{\mathcal{H}}_{2i,2i} + \boldsymbol{\mathcal{H}}_{2i+1,2i+1}\right) \cos (m-n)\theta_i \sim \int_0^1 h_t e^{\text{i}(m-n)\theta_t}dt\end{equation}
同样地,振荡积分的一些估计结果(参考《Oscillatory integrals》、《学习笔记3-一维振荡积分与应用》等)告诉我们,该振荡积分在比较容易达到的条件下,有$|m-n|\to\infty$时积分值趋于零,因此远程衰减特性是可以得到保留的。
如果$\boldsymbol{\mathcal{H}}$不是对角阵,那么很遗憾,上述性质都很难重现的。我们只能寄望于$\boldsymbol{\mathcal{H}}$的对角线部分占了主项,这样一来上述的性质还能近似保留。对角线部分占主项,意味着$d$维向量之间任意两个维度的相关性比较小,满足一定的解耦性。对于Embedding层来说,这个假设还是有一定的合理性的,笔者检验了BERT训练出来的词Embedding矩阵和位置Embedding矩阵的协方差矩阵,发现对角线元素明显比非对角线元素大,证明了对角线元素占主项这个假设具有一定的合理性。
问题讨论 #
有读者会反驳:就算你把Sinusoidal位置编码说得无与伦比,也改变不了直接训练的位置编码比Sinusoidal位置编码效果要好的事实。的确,有实验表明,在像BERT这样的经过充分预训练的Transformer模型中,直接训练的位置编码效果是要比Sinusoidal位置编码好些,这个并不否认。本文要做的事情,只是从一些原理和假设出发,推导Sinusoidal位置编码为什么可以作为一个有效的位置,但并不是说它一定就是最好的位置编码。
推导是基于一些假设的,如果推导出来的结果不够好,那么就意味着假设与实际情况不够符合。那么,对于Sinusoidal位置编码来说,问题可能出现在哪呢?我们可以逐步来反思一下。
第一步,泰勒展开,这个依赖于$\boldsymbol{p}$是小量,笔者也在BERT中做了检验,发现词Embedding的平均模长要比位置Embedding的平均模长大,这说明$\boldsymbol{p}$是小量某种程度上是合理的,但是多合理也说不准,因为Embedding模长虽然更大但也没压倒性;第二步,假设$\boldsymbol{\mathcal{H}}$是单位阵,因为上一节我们分析了它很可能是对角线占主项的,所以先假设单位阵可能也不是太大的问题;第三步,假设通过两个绝对位置向量的内积来表达相对位置,这个直觉上告诉我们应该是合理的,绝对位置的相互应当有能力表达一定程度的相对位置信息;最后一步,通过自动远程衰减的特性来确定$\theta_i$,这个本身应该也是好的,但就是这一步变数太大,因为可选的$\theta_i$形式太多,甚至还有可训练的$\theta_i$,很难挑出最合理的,因此如果说Sinusoidal位置编码不够好,这一步也非常值得反思。
文章小结 #
总的来说,本文试图基于一些假设,反推出Sinusoidal位置编码来,这些假设具有其一定的合理性,也有一定的问题,所以相应的Sinusoidal位置编码可圈可点,但并非毫无瑕疵。但不管怎样,在当前的深度学习中,能够针对具体的问题得到一个显式解,而不是直接暴力拟合,Sinusoidal位置编码是一个不可多得的案例,值得我们思考回味。
转载到请包括本文地址:https://kexue.fm/archives/8231
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Mar. 08, 2021). 《Transformer升级之路:1、Sinusoidal位置编码追根溯源 》[Blog post]. Retrieved from https://kexue.fm/archives/8231
@online{kexuefm-8231,
title={Transformer升级之路:1、Sinusoidal位置编码追根溯源},
author={苏剑林},
year={2021},
month={Mar},
url={\url{https://kexue.fm/archives/8231}},
}







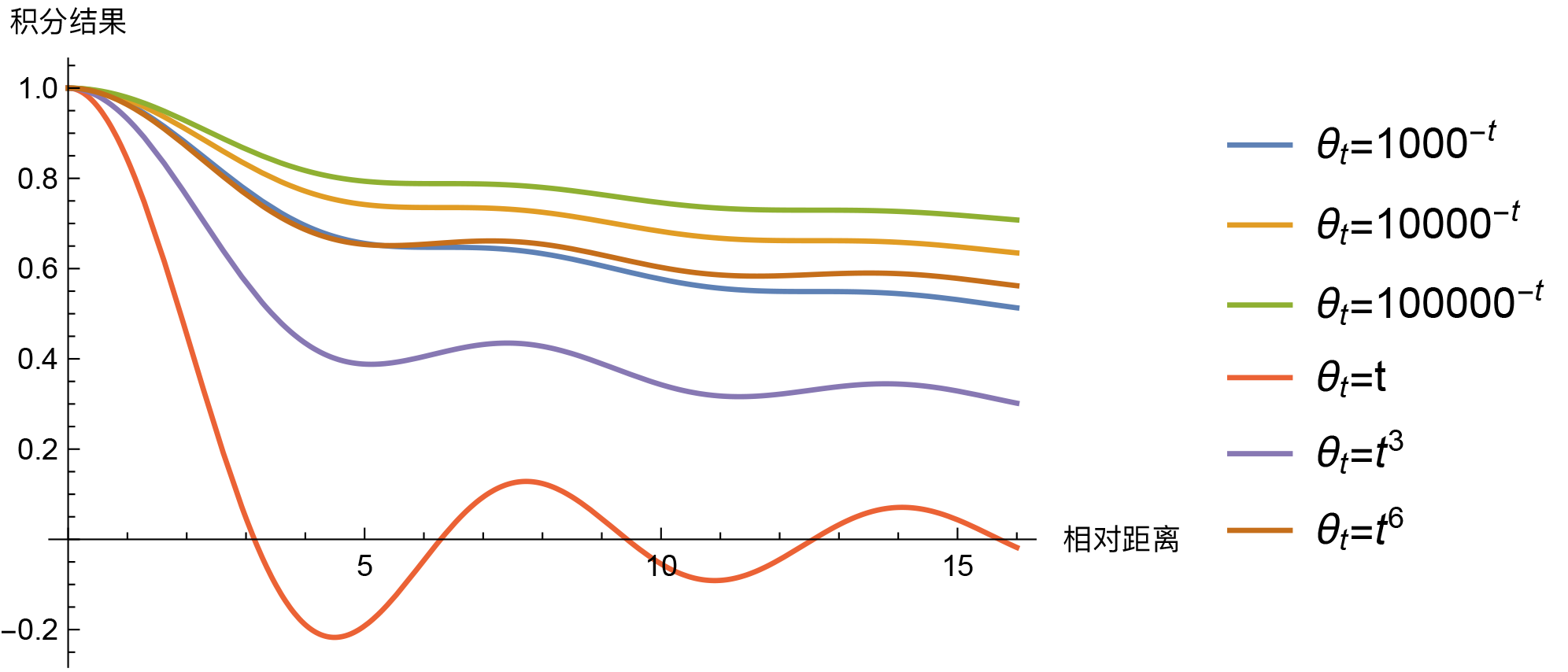



March 4th, 2025
[...]Transformer升级之路:1、Sinusoidal位置编码追根溯源 - 科学空间|Scientific Spaces[...]
March 7th, 2025
苏神,看了Sinusoidal和RoPE,我有一点不理解的是,在二维的情况扩展到D维,既然只是希望是多个二维的组合,而且提到了神经元是无序的,那为什么还需要区分D维度中的每个元素(theta = 10000^(2i/d))?比如直接叠加多个与i无关的二维变换可以么?换句话说,直接叠加D/2个一样的二维编码可以么(会有什么影响么)?
1、可以取$\theta_i=10000^{-2i/d}$然后打乱;
2、所有$\theta_i$取同一个值效果并不好,指数变化的$\theta_i$提供了关于位置的一个层次结构,类似n进制编码,可以参考:https://kexue.fm/archives/9675
感谢苏神
March 10th, 2025
$(4)$的最后一项似乎少了个1/2
没有少,交叉项是重复的,类似$(a+b)^2=a^2+b^2+2ab$。
March 10th, 2025
请问,这里关于位置编码的推导,您是只根据attention paper给出的形式,自己推测的。还是参考了其他什么文章?
之所以问,是因为假如我自己看了attention is all you need 里的公式是想不出来为什么这样的,只能被动接受
主要是受知乎上的纳米酱( https://www.zhihu.com/question/307293465/answer/1028613658 )启发的,至于纳米酱怎么想到的,我也不清楚。
March 30th, 2025
这才是我心中深度学习的样子,花了一小时看懂,酣畅淋漓
May 22nd, 2025
苏神,关于一般情况这个部分我有一些见解,
能不能直接设 $$ \mathcal{H} $$ 是一个对称正定矩阵(如果黑矩阵不是正定的就用复数),存在其平方根矩阵 $$ \mathcal{H}^{1/2} $$,使得:
$$
\mathcal{H} = \mathcal{H}^{1/2} \cdot \mathcal{H}^{1/2}
$$
那么可以将编码向量重新定义为:
$$
\tilde{p}_m = \mathcal{H}^{1/2} p_m
$$
这样就有:
$$
p_m^\top \mathcal{H} p_n = \tilde{p}_m^\top \tilde{p}_n
$$
换句话说,任意 $$ \mathcal{H} $$ 的作用等价于先做一个线性变换(即将编码向量映射到另一个坐标系),之后再用普通内积。
因此我们可以在不丢失一般性的前提下,把问题简化为 $$ \mathcal{H} = I $$。
但你这时候要构造的是$\langle\boldsymbol{\mathcal{H}}^{1/2}\boldsymbol{p}_m, \boldsymbol{\mathcal{H}}^{1/2}\boldsymbol{p}_n\rangle = g(m-n)$,无法得出数据无关的$\boldsymbol{p}_m,\boldsymbol{p}_n$?