用傅里叶级数拟合一维概率密度函数

在《“闭门造车”之多模态思路浅谈（一）：无损输入》中我们曾提到，图像生成的本质困难是没有一个连续型概率密度的万能拟合器。当然，也不能说完全没有，比如高斯混合模型（GMM）理论上就是可以拟合任意概率密度，就连GAN本质上也可以理解为混合了无限个高斯模型的GMM。然而，GMM尽管理论上的能力是足够的，但它的最大似然估计会很困难，尤其是通常不适用基于梯度的优化器，这限制了它的使用场景。

近日，Google的一篇新论文《Fourier Basis Density Model》针对一维情形，提出了一个新的解决方案——用傅里叶级数来拟合。论文的分析过程颇为有趣，构造形式也很是巧妙，值得学习一番。

问题简述 #

可能有读者质疑：只研究一维情形有什么价值？确实，如果只考虑图像生成场景，那可能真的价值有限，但一维概率密度估计本身有它的应用价值，如数据的有损压缩，所以它依然是一个值得研究的主题。再者，即便我们需要研究多维的概率密度，也可以通过自回归的方式转化为多个一维的条件概率密度来估计。最后，这个分析和构造过程本身就很值得回味，所以哪怕是仅仅作为一道数学分析题来练习也是相当有益的。

言归正传。所谓一维概率密度估计，是指给定$n$个从同一分布采样出来的实数$x_1,x_2,\cdots,x_n$的情况下，估计采样分布的概率密度函数。这个问题的方法可以分为“非参数化估计”和“参数化估计”两类。非参数化估计主要就是指核密度估计，它跟《用狄拉克函数来构造非光滑函数的光滑近似》一样，本质上是利用狄拉克函数做光滑近似：
\begin{equation}p(x) = \int p(y)\delta(x - y) = \mathbb{E}_{y\sim p(y)}[\delta(x - y)]\approx \frac{1}{n}\sum_{i=1}^n \delta(x - x_i)\label{eq:delta}\end{equation}
但是$\delta(x - y)$不是常规的光滑函数，所以我们要找它的一个光滑近似，比如$\frac{e^{-(x-y)^2/2\sigma^2}}{\sqrt{2\pi}\sigma}$，它是正态分布的概率密度函数，当$\sigma\to 0$的时候它就是$\delta(x-y)$，代入到上式，结果就是“高斯核密度估计”。

可以看到，核密度估计本质上就是把数据背下来，因此可以推测它泛化能力有限，另外它的复杂度正比于数据量，那么数据规模较大时也不实用，所以我们需要“参数化估计”，即构建一个非负的、归一化的、带有固定量的参数$\theta$的概率密度函数簇$p_{\theta}(x)$，然后通过最大似然就可以求解：
\begin{equation}\theta^* = \mathop{\text{argmax}}_{\theta} \sum_{i=1}^n \log p_{\theta}(x_i)\end{equation}
这个问题的关键就是如何构建一簇有足够拟合能力的概率密度函数$p_{\theta}(x)$。

已有方法 #

参数化概率密度估计的经典方法是高斯混合模型（Gaussian Mixed Model，GMM），它的出发点同样是式$\eqref{eq:delta}$加高斯核，但它不是遍历所有数据作为中心，而是通过训练的方式，找到有限的$K$个均值和方差，构建一个复杂度跟数据量无关的模型：
\begin{equation}p_{\theta}(x) = \frac{1}{K}\sum_{i=1}^K \frac{e^{-(x-\mu_i)^2/2\sigma_i^2}}{\sqrt{2\pi}\sigma_i},\quad \theta = \{\mu_1,\sigma_1,\mu_2,\sigma_2,\cdots,\mu_K,\sigma_K\}\end{equation}
GMM通常也被理解为一种聚类方法，它是K-Means的推广，$\mu_1,\mu_2,\cdots,\mu_K$是聚类中心，比K-Means则多出了方差$\sigma_1,\sigma_2,\cdots,\sigma_K$。由于式$\eqref{eq:delta}$的理论保证，因此当$K$足够大、$\sigma$足够小时，GMM理论上总能拟合任意复杂的分布，因此GMM的理论能力是足够的。但GMM的问题在于$e^{-(x-\mu_i)^2/2\sigma_i^2}$这个形式衰减得太快，梯度消失非常严重，因此通常只能用EM算法求解（参考《三味Capsule：矩阵Capsule与EM路由》），不好用梯度优化器优化，这限制了它的应用，而且即便用EM算法也通常都只能找到一个次优的解。

原论文还提到了一个叫做DFP（Deep Factorized Probability）的方法，它是专为一维概率密度估计设计的，出自论文《Variational image compression with a scale hyperprior》。DFP利用了累积概率函数的单调性，即如下积分
\begin{equation}\Phi(x) = \int_{-\infty}^x p(y)dy \in [0,1]\end{equation}
必然是单调递增的。如果我们能先构造一个$\mathbb{R}\mapsto[0,1]$的单调递增函数$\Phi_{\theta}(x)$，那么对它求导就是一个合理的概率密度函数。如何保证一个模型的输出随着输入单调递增呢？DFP用一个多层神经网络来构建模型，并且保证：1、所有激活函数都是单调递增的；2、所有乘法权重都是非负的。在这两点约束之下，模型必然符合单调递增这一特点，最后再加个Sigmoid，就可以控制值域为$[0,1]$。

DFP的原理也称得上是简单直观，但类似于flow-based模型，这种逐层的约束会让人担心损失了拟合能力。此外，由于该模型完全由神经网络构建，根据此前《Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks》等结论，神经网络在训练时会优先学习低频信号，这可能会使得DPF对概率密度的峰值点拟合不佳，即出现过度平滑的拟合结果，然而在很多场景下，峰值的拟合能力是衡量一个概率建模方法的重要指标之一。

请傅里叶 #

如论文标题“Fourier Basis Density Model”（下面简称FBDM）所示，论文所提的新方法，是基于傅里叶级数来拟合概率密度的。有一说一，其实用傅里叶级数来拟合这一点并不难想到，难的是里边有一个关键的非负约束不容易构造，而FBDM则是把相关的细节都走通了，不得不让人佩服。

简单起见，我们把$x$的定义域设为$[-1,1]$，由于总可以通过$\tanh$之类的变换将$\mathbb{R}$上的实数都压到到$[-1,1]$，因此这个设定并不失一般性。也就是说，现在我们所求的概率密度函数$p(x)$是定义在$[-1,1]$上的函数，那么我们可以将它写成傅里叶级数
\begin{equation}p(x) = \sum_{n=-\infty}^{\infty} c_n e^{i\pi n x},\quad c_n = \frac{1}{2}\int_{-1}^1 p(x) e^{-i\pi n x} dx\end{equation}
然而，我们现在要做的事情是反过来的，并非已知$p(x)$求它的傅里叶级数，而是只知道$p(x)$的样本，需要把$p(x)$设成如下的截断傅里叶级数形式，然后把系数$c_n$通过优化器求出来：
\begin{equation}f_{\theta}(x) = \sum_{n=-N}^{N} c_n e^{i\pi n x},\quad \theta = \{c_{-N},c_{-N+1},\cdots,c_{N-1},c_N\}\label{eq:fourier-series}\end{equation}
众所周知，作为一个合理的概率密度函数，$f_{\theta}(x)$至少要满足如下两个条件：
\begin{equation}\text{非负:}\,\,f_{\theta}(x)\geq 0,\quad \text{归一:}\,\,\int_{-1}^1 f_{\theta}(x)dx = 1\end{equation}
问题是如果$c_n$取任意实数/复数，那么式$\eqref{eq:fourier-series}$是否实数都无法保证，更不用说非负了。所以说，用傅里叶级数来拟合并不难想，难在如何设定$c_n$的形式，使得对应的输出必然是非负的（后面我们将会看到，在傅里叶级数下，最难的是非负，归一反而简单）。

保证非负 #

这一节我们就来看全文难度最高的非负性构造。当然，这里的难并不是说它推导有多复杂，而是非常有技巧性。

首先，我们知道非负的前提是实数，而保证实数相对比较简单：
\begin{equation}c_n^* = \left[\frac{1}{2}\int_{-1}^1 p(x) e^{-i\pi n x} dx\right]^* = \frac{1}{2}\int_{-1}^1 p(x) e^{i\pi n x} dx = c_{-n}\end{equation}
可以反过来证明这个条件也是充分的，所以保证实数只需要约束$c_n^* = c_{-n}$，这个相对来说很容易实现，同时这也意味着式$\eqref{eq:fourier-series}$的级数作为概率密度函数时，只有$c_0,c_1,\cdots,c_N$这$N+1$个独立参数。

关于非负约束，原论文只是抛出了一个“Herglotz’s theorem”的引用，然后就直接给出了答案，可以说几乎没有推导。笔者搜了一下Herglotz’s theorem，也发现鲜有介绍，因此只好尝试跳过Herglotz’s theorem，用自己的方式去理解原论文的答案了。

考虑任意整数的有限子集$\mathbb{K}\subseteq\mathbb{N}$，以及对应的任意复数列$\{u_k|k\in\mathbb{K}\}$，我们有
\begin{equation}\begin{aligned}
\sum_{n,m\in \mathbb{K}} u_n^* c_{n-m} u_m =&\, \sum_{n,m\in \mathbb{K}} u_n^* \left[\frac{1}{2}\int_{-1}^1 p(x) e^{-i\pi (n-m) x} dx\right] u_m \\
=&\, \frac{1}{2}\int_{-1}^1 p(x) \left[\sum_{n,m\in \mathbb{K}} u_n^* e^{-i\pi (n-m) x} u_m \right] dx \\
=&\, \frac{1}{2}\int_{-1}^1 p(x) \sum_{n,m\in \mathbb{K}} \left[(u_n e^{i\pi n})^* (u_m e^{i\pi m})\right] dx \\
=&\, \frac{1}{2}\int_{-1}^1 p(x) \left[\left(\sum_{n\in \mathbb{K}}u_n e^{i\pi n}\right)^* \left(\sum_{m\in \mathbb{K}}u_m e^{i\pi m}\right)\right] dx \\
=&\, \frac{1}{2}\int_{-1}^1 p(x) \left|\sum_{n\in \mathbb{K}}u_n e^{i\pi n}\right|^2 dx \\
\geq&\, 0 \\
\end{aligned}\end{equation}
最后的$\geq 0$取决于$p(x)\geq 0$，所以我们就得出了$f_{\theta}(x)\geq 0$的一个必要条件：$\sum\limits_{n,m\in \mathbb{K}} u_n^* c_{n-m} u_m\geq 0$。如果将所有$c_{n-m}$排列成一个大矩阵（Toeplitz矩阵），那么这个条件用线性代数的话说就是任意$\mathbb{K}$对应的行列交集组成的子矩阵都是复空间中的正定矩阵。也可以证明这个条件是充分的，即满足此条件的$f_{\theta}(x)$必然恒大于0。

所以问题变成了如何找一个复数列$\{c_n\}$，使得对应的Toeplitz矩阵$\{c_{n-m}\}$是一个正定矩阵。看上去这转换把问题变得更加复杂了，但对于了解时间序列的读者来说，他们可能知道一个现成的构造方式，那就是“自相关系数”：对于任意复数列$\{a_k\}$，自相关系数定义为
\begin{equation}r_n = \sum_{k=-\infty}^{\infty} a_k a_{k+n}^*\end{equation}
可以证明$r_{n-m}$必然是正定的：
\begin{equation}\begin{aligned}
\sum_{n,m\in \mathbb{K}} u_n^* r_{n-m} u_m =&\, \sum_{n,m\in \mathbb{K}} u_n^* \left(\sum_{k=-\infty}^{\infty} a_k a_{k+n-m}^*\right) u_m \\
=&\, \sum_{n,m\in \mathbb{K}} u_n^* \left(\sum_{k=-\infty}^{\infty} a_{k+m} a_{k+n}^*\right) u_m \\
=&\, \sum_{k=-\infty}^{\infty}\left(\sum_{n\in \mathbb{K}} a_{k+n} u_n\right)^*\left(\sum_{m\in \mathbb{K}} a_{k+m} u_m\right) \\
=&\, \sum_{k=-\infty}^{\infty}\left|\sum_{n\in \mathbb{K}} a_{k+n} u_n\right|^2 \\
\geq&\, 0
\end{aligned}\end{equation}
因此将$c_n$取成$r_n$的形式就是一个可行的解。为了确保$c_n$的独立参数量只有$N+1$个，我们约定当$k < 0$或者$k > N$时$a_k=0$，那么得到
\begin{equation}c_n = \sum_{k=0}^{N-n} a_k a_{k+n}^*\end{equation}
这就构成出了对应的$c_n$，使得式$\eqref{eq:fourier-series}$的傅里叶级数的结果必然非负，满足了概率密度函数的非负要求。

一般结果 #

至此，整个问题中最难的部分——“非负性”已经被解决。剩下的归一化很简单，因为
\begin{equation}\int_{-1}^1 f_{\theta}(x)dx = \int_{-1}^1 \sum_{n=-N}^{N} c_n e^{i\pi n x} dx = 2c_0\end{equation}
所以归一化因子就是$2c_0$！于是我们只需要将$p_{\theta}(x)$设成
\begin{equation}
p_{\theta}(x) = \frac{f_{\theta}(x)}{2c_0}=\frac{1}{2} + \sum_{n=1}^{N} \frac{c_n e^{i\pi n x} + c_{-n}e^{-i\pi n x}}{2c_0} = \text{Re}\left[\frac{1}{2} + \sum_{n=1}^N \frac{c_n}{c_0} e^{i\pi n x}\right], \\
c_n = \sum_{k=0}^{N-n} a_k a_{k+n}^*,\quad\theta = \{a_0,a_1,\cdots,a_N\}\end{equation}
它就是一个有效的概率密度候选函数。

当然，目前这个分布还只是定义在$[-1,1]$，我们需要将它扩展到整个$\mathbb{R}$上，这个不难，我们先想一个将$\mathbb{R}$压缩为$[-1,1]$的变换，然后求变换之后的概率密度形式就行。为此，我们可以先通过原始样本估计出均值$\mu$和方差$\sigma^2$，然后通过$x=\frac{y-\mu}{\sigma}$就将它变为均值为0、方差为1的分布，接着就可以通过$x=\tanh\left(\frac{y-\mu}{\sigma}\right)$压缩到$[-1,1]$中，对应的新概率密度函数为
\begin{equation}q_{\theta}(y) = p_{\theta}(x)\frac{dx}{dy} = \frac{1}{\sigma}\text{sech}^2\left(\frac{y-\mu}{\sigma}\right) p_{\theta}\left(\tanh\left(\frac{y-\mu}{\sigma}\right)\right)\end{equation}
从端到端学习的角度来讲，我们可以直接把原始数据代入到$q_{\theta}(y)$的对数似然中进行优化（而不是先压缩后优化），甚至可以连同$\mu,\sigma$也当成可训练参数一起调整。

最后，为了防止过拟合，我们还需要一个正则项，正则项的目的是希望拟合的分布能稍微平滑一些，不要过度陷入局部细节中，为此，我们考虑$f_{\theta}(x)$导数的模长平方作为正则项：
\begin{equation}\gamma\int_{-1}^1 \left|\frac{df_{\theta}(x)}{dx}\right|^2 = \gamma\sum_{n=-N}^N 2\pi^2 n^2 |c_n|^2 dx\end{equation}
从最后的形式可以看出，它加大了高频项系数的惩罚权重，这可以避免模型过度拟合高频细节，从而提高泛化能力。

延伸思考 #

到这里，我们已经把FBDM的所有理论推导完成了，剩下的自然是做实验，这部分我们不再重复，直接看原文的结果就好。注意FBDM的所有系数和运算都是在复数域内，如果强行实数化会让结果形式复杂不少，所以简单起见应该直接基于所用框架的复数运算来实现（原论文用的是Jax）。

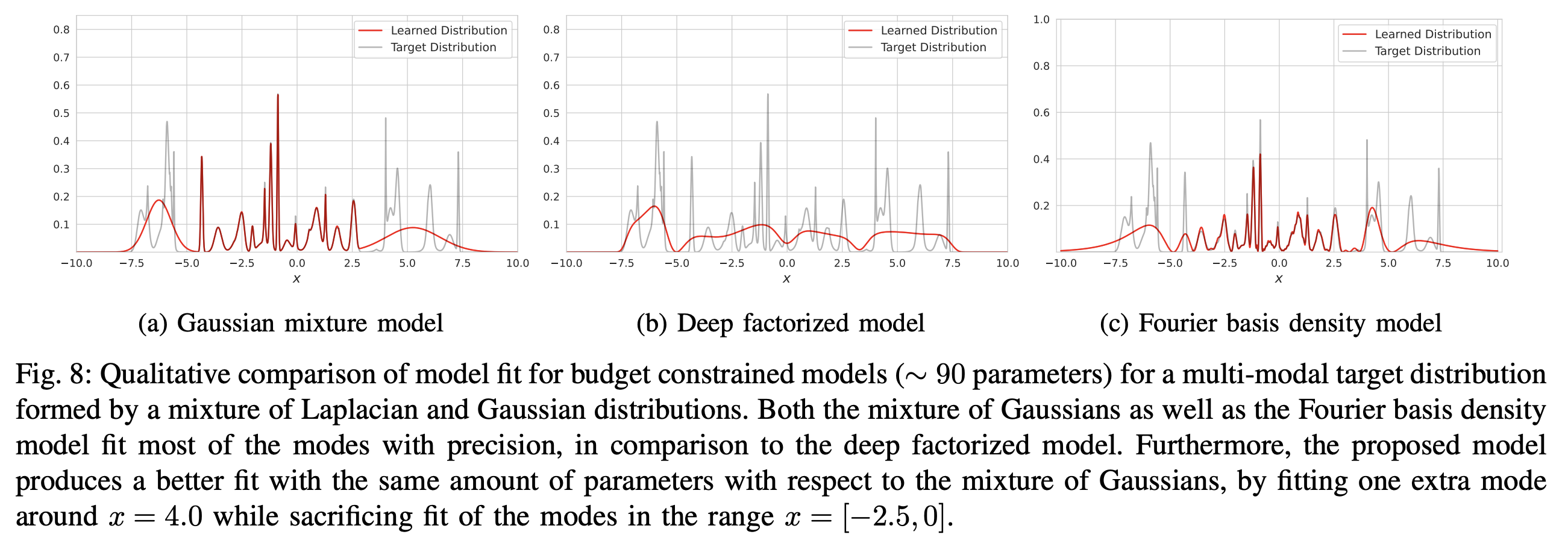
在看实验结果之前，我们先来想想评价指标是什么。如果是模拟实验的话，我们通常都能知道真实分布的概率密度表达式，因此最直接的指标就是计算真实分布与拟合分布的KL散度/W距离等分布度量。除此之外，对于概率密度的拟合，我们通常有一个更关心的指标，那就是“峰值”的拟合效果。假设概率密度是光滑的，那么它可能有多个局部最大值点，这些局部最大值点就是我们所说的峰值，或者称为“modal”，很多场景下能否准确找到更多的modal比整个分布的度量大小更重要，比如有损压缩的基本思想就是只保留这些modal来描述分布。

而从原论文的实验结果可以看到，在同等参数量下FBDM在KL散度和modal方面都做得更好：

之所以有这样的优势，笔者猜测是因为FBDM的虚指数形式，本质上就是三角函数，它不像GMM那样的负指数有严重的梯度消失问题，因此基于梯度的优化器有更大的概率能找到更优的解答。从这个形式来看，FBDM也可以理解为连续型概率密度的“Softmax”，都是以$\exp$为基来构建一个概率分布，只不过一个是实指数，一个则是虚指数。

相比GMM，FBDM自然也有一些缺点，如不够直观、不易采样、不易推广到高维等（当然这些缺点DFP也有）。GMM很直观，就是有限个正态分布的加权平均的形式，通过先类别采样、后正态采样的层次采样就可以实现概率密度函数中采样，相比之下FBDM没那么直观的方案，看上去只能通过逆累积概率函数的方式进行采样，即先求出累积概率函数
\begin{equation} \Phi(x) = P(\leq x) = \int_{-1}^x p_{\theta}(x)dx = \frac{x^2-1}{2} + \frac{1}{2}\sum_{n=1}^{N} \frac{c_n}{c_0} \frac{e^{i\pi n x} - (-1)^n}{i\pi n}\end{equation}
然后$y=\Phi^{-1}(\varepsilon),\varepsilon\sim U[0,1]$就可以实现采样了。至于高维推广，正态分布本来就有高维形式，因此GMM推广到任意维度也很容易，但是FBDM要想直接推广到$D$维，那么就有$(N+1)^D$个参数，很明显复杂度太高，或者就像Decoder-Only的LLM一样，用自回归的方式转化为多个一维条件概率密度估计，总之，办法不能说没有，但是各种弯弯绕绕更多。

文章小结 #

本文介绍了一种用傅里叶级数来建模一维概率密度函数的新思路，关键之处是通过精巧的系数构造，来约束原本值域是复数域的傅里叶级数成为一个非负函数，整个过程颇为赏心悦目，值得学习一番。

转载到请包括本文地址：https://kexue.fm/archives/10007

更详细的转载事宜请参考：《科学空间FAQ》