用狄拉克函数来构造非光滑函数的光滑近似

在机器学习中，我们经常会碰到不光滑的函数，但我们的优化方法通常是基于梯度的，这意味着光滑的模型可能更利于优化（梯度是连续的），所以就有了寻找非光滑函数的光滑近似的需求。事实上，本博客已经多次讨论过相关主题，比如《寻求一个光滑的最大值函数》、《函数光滑化杂谈：不可导函数的可导逼近》等，但以往的讨论在方法上并没有什么通用性。

不过，笔者从最近的一篇论文《SAU: Smooth activation function using convolution with approximate identities》学习到了一种比较通用的思路：用狄拉克函数来构造光滑近似。通用到什么程度呢？理论上有可数个间断点的函数都可以用它来构造光滑近似！个人感觉还是非常有意思的。

狄拉克函数 #

在很早之前的文章《诡异的Dirac函数》中，我们就介绍过狄拉克函数了。在现代数学中，狄拉克函数被定义为一个“泛函”而不是“函数”，但对于大多数读者来说，将它当作函数来理解是比较容易接受的。

简单来说，狄拉克函数$\delta(x)$满足：

1、$\forall x\neq 0, \delta(x) = 0$；

2、$\delta(0) = \infty$；

3、$\int_{-\infty}^{\infty} \delta(x) dx = 1$。

直观来看，$\delta(x)$可以看成一个连续型的概率密度函数，采样空间为全体实数$\mathbb{R}$，但是只有$x=0$处概率非零，也即均值为0、方差也为0，所以从中采样必然只能采样到0，因此成立如下恒等式：
\begin{equation}\int_{-\infty}^{\infty} f(x)\delta(x) dx = f(0)\end{equation}
或者
\begin{equation}\int_{-\infty}^{\infty} f(y)\delta(x-y) dy = f(x)\label{eq:base}\end{equation}
这可谓是狄拉克函数最重要的性质，也是我们后面主要用到的恒等式。

光滑近似 #

如果我们能找到$\delta(x)$的一个光滑近似$\varphi(x)\approx \delta(x)$，那么根据$\eqref{eq:base}$，我们就有
\begin{equation}g(x) = \int_{-\infty}^{\infty} f(y)\varphi(x-y) dy \approx f(x)\end{equation}
由于$\varphi(x)$是光滑的，所以$g(x)$也是光滑的，这也就是说，$g(x)$就是$f(x)$的一个光滑近似！这便是借助狄拉克函数的光滑近似来构建$f(x)$的光滑近似的核心思路了，在这个过程中，对$f(x)$的形式和连续性都没有太多限制，比如允许$f(x)$有可数个间断点（如取整函数$[x]$）。

那么狄拉克函数的光滑近似有哪些呢？现成的也有不少，比如：
\begin{equation}\delta(x) = \lim_{\sigma\to 0} \frac{e^{-x^2/2\sigma^2}}{\sqrt{2\pi}\sigma}\label{eq:g}\end{equation}
或
\begin{equation}\delta(x)=\frac{1}{\pi} \lim_{a \to 0}\frac{a}{x^2+a^2}\end{equation}
简单来说，就是找一个像正态分布那样钟形曲线的非负函数，想办法让钟形的宽度逐渐趋于0，但保持积分为1。还有另一个思路是留意到
\begin{equation}\int_{-\infty}^x \delta(t)dt = \theta(x) = \left\{\begin{aligned}1,\,\, (x > 0) \\ 0,\,\, (x < 0)\end{aligned}\right.\end{equation}
也就是说，狄拉克函数的积分是“单位阶跃函数”$\theta(x)$，如果我们能找到$\theta(x)$的光滑近似，那么将它求导就得到狄拉克函数的光滑近似。而$\theta(x)$的光滑近似，就是所谓的“S形”曲线了，比如sigmoid函数$\sigma(x)=1/(1+e^{-x})$，所以我们有
\begin{equation}\delta(x) = \lim_{t\to \infty} \frac{d}{dx}\sigma(tx) = \lim_{t\to \infty} \frac{e^{tx}t}{(1+e^{tx})^2}\label{eq:s}\end{equation}
常用的就是式$\eqref{eq:g}$和式$\eqref{eq:s}$两个近似。

ReLU激活 #

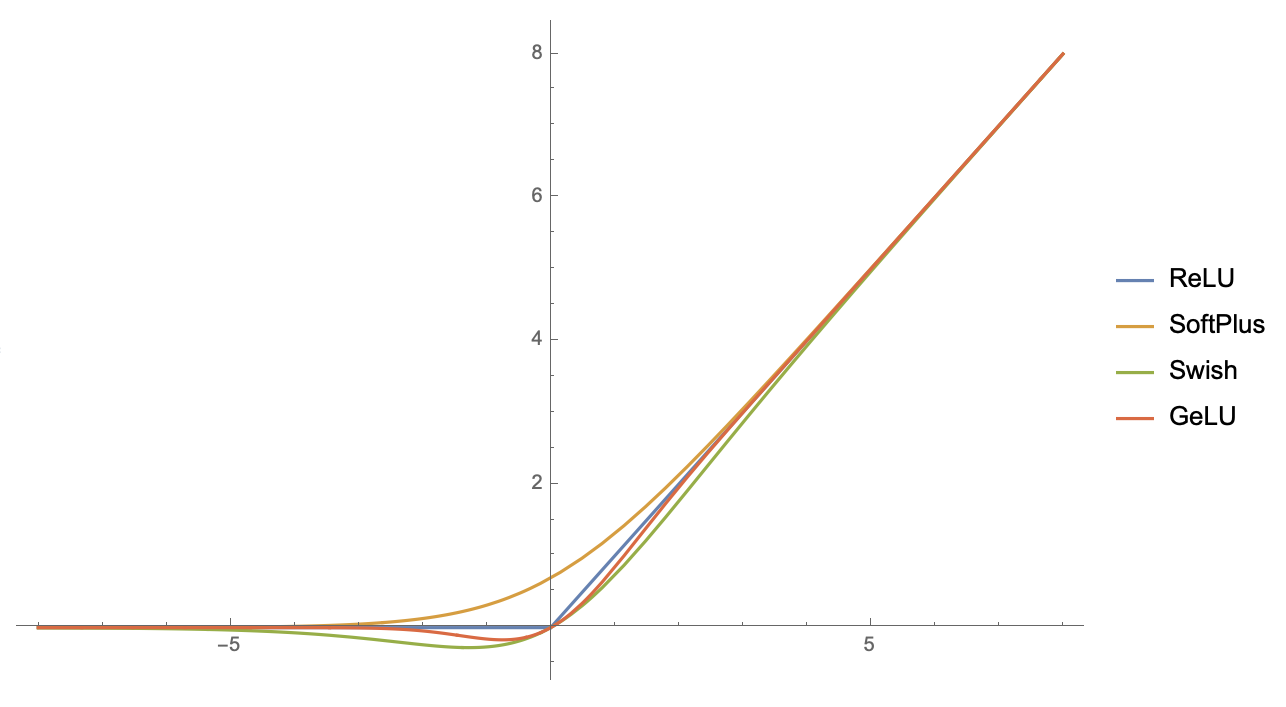
现在，我们就以上述思路为工具，推导ReLU激活函数$\max(x,0)$的各种光滑近似。

比如利用式$\eqref{eq:s}$，得到
\begin{equation}\begin{aligned}
\max(x,0)\approx&\, \int_{-\infty}^{\infty} \frac{e^{t(x-y)}t}{(1+e^{t(x-y)})^2} \max(y,0) dy\\
=&\,\int_0^{\infty} \frac{e^{t(x-y)}ty}{(1+e^{t(x-y)})^2}dy=\frac{\log(1+e^{tx})}{t}
\end{aligned}\end{equation}
当$t=1$时，这便是SoftPlus激活函数。

如果换用式$\eqref{eq:g}$，那么结果是
\begin{equation}\begin{aligned}
\max(x,0)\approx&\, \int_{-\infty}^{\infty} \frac{e^{-(x-y)^2/2\sigma^2}}{\sqrt{2\pi}\sigma} \max(y,0) dy\\
=&\,\int_0^{\infty} \frac{e^{-(x-y)^2/2\sigma^2} y}{\sqrt{2\pi}\sigma}dy\\
=&\,\frac{1}{2} \left[x \,\text{erf}\left(\frac{x}{\sqrt{2} \sigma}\right)+x+\sqrt{\frac{2}{\pi }} \sigma e^{-\frac{x^2}{2 \sigma^2}}\right]
\end{aligned}\end{equation}
这个ReLU的光滑近似貌似还没被研究过。

当然，如果仅仅是ReLU函数的光滑近似，那么还有更简单的思路，比如留意到$\max(x,0)=x\theta(x)$，这里的$\theta(x)$就是前面提到的单位阶跃函数，所以问题可以转变为求$\theta(x)$的光滑近似，我们已经知道sigmoid便是其中之一，所以很快得到
\begin{equation}\max(x,0)\approx x\sigma(tx)\end{equation}
当$t=1$时，这便是Swish激活函数。而如果用$\eqref{eq:g}$进行计算，那么就得到
\begin{equation}\begin{aligned}
\max(x,0)\approx&\, x\int_{-\infty}^{\infty} \frac{e^{-(x-y)^2/2\sigma^2}}{\sqrt{2\pi}\sigma} \theta(y) dy\\
=&\,x\int_0^{\infty} \frac{e^{-(x-y)^2/2\sigma^2}}{\sqrt{2\pi}\sigma}dy =\frac{1}{2}\left[x + x\,\text{erf}\left(\frac{x}{\sqrt{2}\sigma}\right)\right]
\end{aligned}\end{equation}
当$\sigma=1$时，就是GeLU激活函数。

ReLU函数及其几个光滑近似的图像

取整函数 #

可能读者觉得还不够意思，毕竟上面推导出来的都是现成的东西，而且不借助狄拉克函数也能推导出来。现在我们就来补充一个不怎么平凡的例子：取整函数的光滑近似。

取整函数分上取整和下取整两种，它们定义上有所不同，但是没有本质区别，这里以下取整为例子，我们记为
\begin{equation}[x] = n, \,\,\text{当且仅当存在}n\in\mathbb{Z}\text{使得}x\in[n, n + 1)\end{equation}

假设$\varphi(x)$为狄拉克函数的某个光滑近似，那么
\begin{equation}
[x]\approx \int_{-\infty}^{\infty} \varphi(x-y)[y]dy = \sum_{n=-\infty}^{\infty}n\int_n^{n+1} \varphi(x-y)dy\end{equation}
设$\varphi(x)$的原函数为$\Phi(x)$，那么$\varphi(x-y)$关于$y$的原函数就是$-\Phi(x-y)$，于是有
\begin{equation}\begin{aligned}[]
[x]\approx&\,\sum_{n=-\infty}^{\infty}n\big[\Phi(x-n) - \Phi(x-n-1)\big]\\
=&\,\lim_{M,N\to\infty}\sum_{n=-M}^{N}(n-1)\Phi(x-n) - n\Phi(x-n-1) + \Phi(x-n)\\
=&\,\lim_{M,N\to\infty} -N\Phi(x-N-1) - (M+1)\Phi(x+M) + \sum_{n=-M}^{N} \Phi(x-n)
\end{aligned}\end{equation}
对于$\Phi(x)$我们有$\Phi(-\infty)=0$和$\Phi(\infty)=1$，所以假设我们关心的范围满足$-M\ll x \ll N$，那么$\Phi(x-N-1)\approx 0$和$\Phi(x+N)\approx 1$，所以此时：
\begin{equation}\begin{aligned}[]
[x]\approx&\, -M-1 + \sum_{n=-M}^{N} \Phi(x-n)\\
=&\,\sum_{n=-M}^0 \big[\Phi(x-n)-1\big] + \sum_{n=1}^N \Phi(x-n)
\end{aligned}\end{equation}
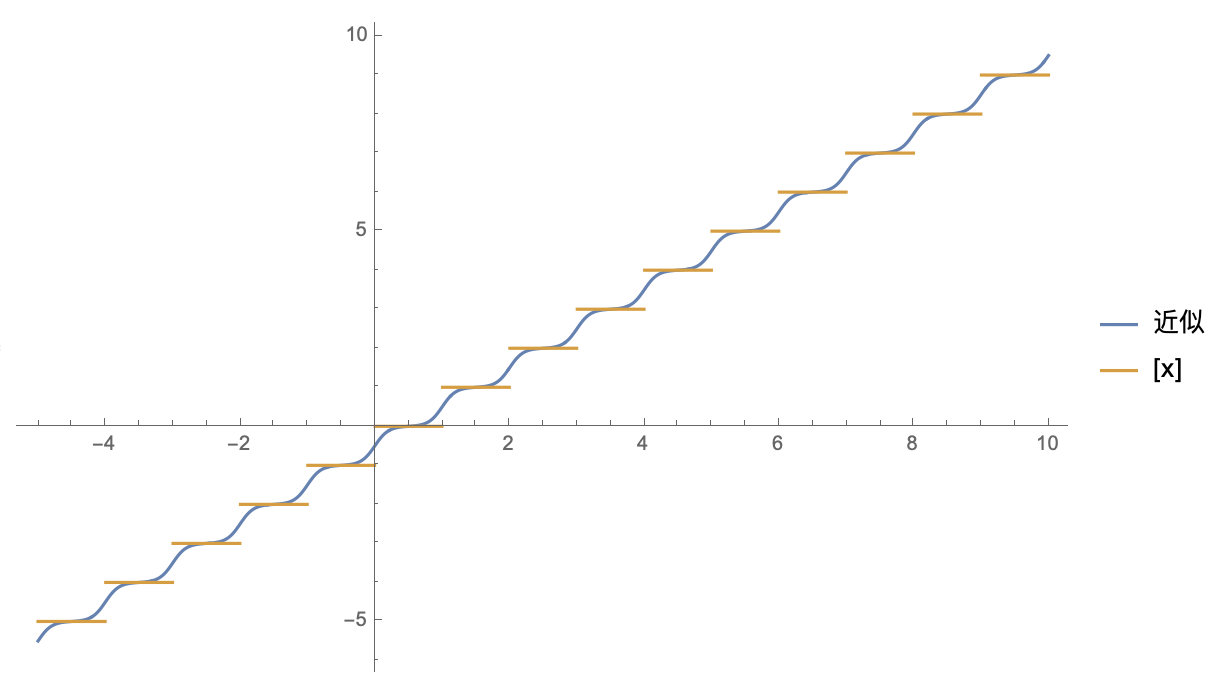
用$\Phi(x)=\sigma(tx)$作为例子，取$t=10,M=5,N=10$，结果如下：

取整函数的光滑近似效果

可以看到，确实与$[x]$蛮近似的，增大$t$能进一步提高近似程度。

文章小结 #

本文介绍了一种利用狄拉克函数来构造光滑近似的方法，其特点是比较通用，对原函数没有太严格的要求。作为例子，我们利用它导出了ReLU函数的各种常见近似以及取整函数的一个光滑近似。

转载到请包括本文地址：https://kexue.fm/archives/8718

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。