在学车的时候，我堂大哥曾问我一道作圆的问题：

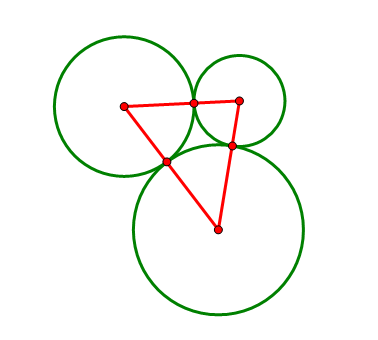
三圆的外切圆和内切圆 (1)

三圆的外切圆和内切圆 (1)

平面上给出三个两两相切的圆以及它们的圆心，求作一个圆与这三个圆都相切（尺规作图）。

如果从纯几何的途径入手，我们甚至很难判断这样的圆是否存在。但是我之前似乎已经看过类似的题目，于是很快想到一个名词：反演。反演可以将圆反演成直线（圆过反演点），也可以将圆反演成圆（圆不过反演点），而其他的相切、相交等关系保持不变。对反演后的图形进行相同的反演，就变回原来的图形。本题的难点在于圆太多，利用反演，我们可以将它变为两条直线和一个圆的问题。

假设读者已经有了反演的基本知识，如果没有，请到
http://zh.wikipedia.org/wiki/反演

阅读相关内容。

下面是作图步骤：

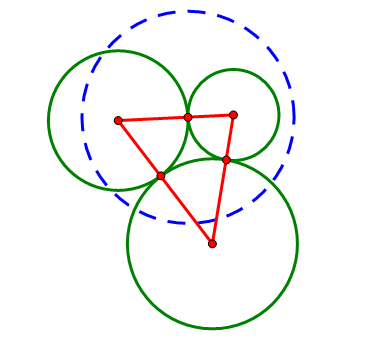
(1) 选择一个相切点，以相切点为圆心作一个圆（半径随意）；

三圆的外切圆和内切圆 (2)

三圆的外切圆和内切圆 (2)

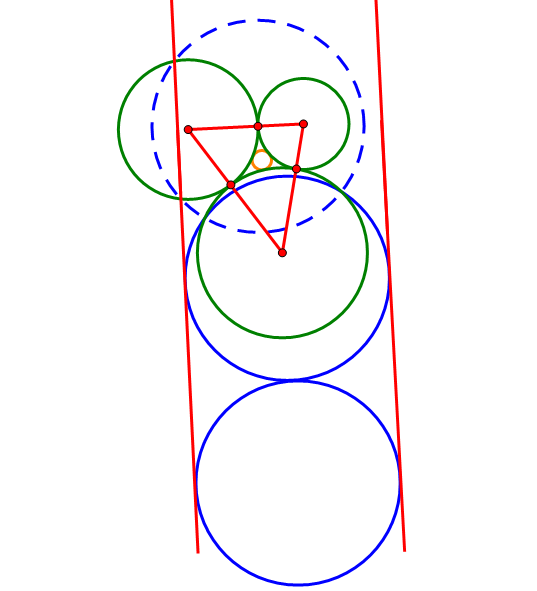
(2) 以(1)作的圆为基础圆，作给出的三个圆的反演像。其中两个圆变为两条平行直线，第三个圆依旧反演为圆，并与两直线相切。

三圆的外切圆和内切圆 (3)

三圆的外切圆和内切圆 (3)

三圆的外切圆和内切圆 (4)

三圆的外切圆和内切圆 (4)

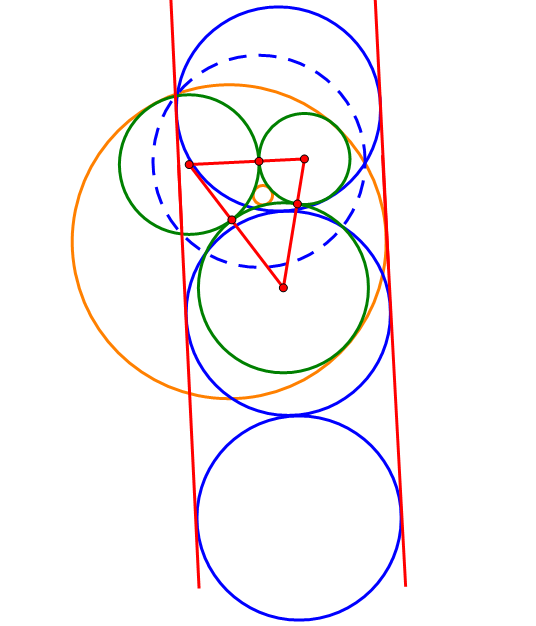
(3)接下来的步骤就很容易了，显然我们可以作出两个圆，与反演像中的圆和两条直线都相切。作出这两个圆后，继续以(1)的圆为基础圆，将这两个圆反演回去，就得到了所求的圆，分别对应着三个圆的外切圆和内切圆。

三圆的外切圆和内切圆 (5)

三圆的外切圆和内切圆 (5)

三圆的外切圆和内切圆 (6)

三圆的外切圆和内切圆 (6)

转载到请包括本文地址：https://kexue.fm/archives/2320

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jan. 27, 2014). 《三个相切圆的公切圆 》[Blog post]. Retrieved from https://kexue.fm/archives/2320

@online{kexuefm-2320,
        title={三个相切圆的公切圆},
        author={苏剑林},
        year={2014},
        month={Jan},
        url={\url{https://kexue.fm/archives/2320}},
}