这一次又是数联天地论坛上的问题，这个数学论坛做的挺好的。^_^

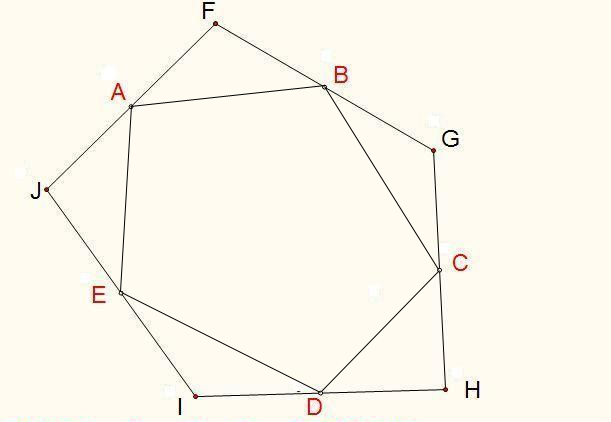
已知五个定点A、B、C、D、E，求作五边形FGHIJ，使每一边的中点分别为5定点。

五边形问题

五边形问题

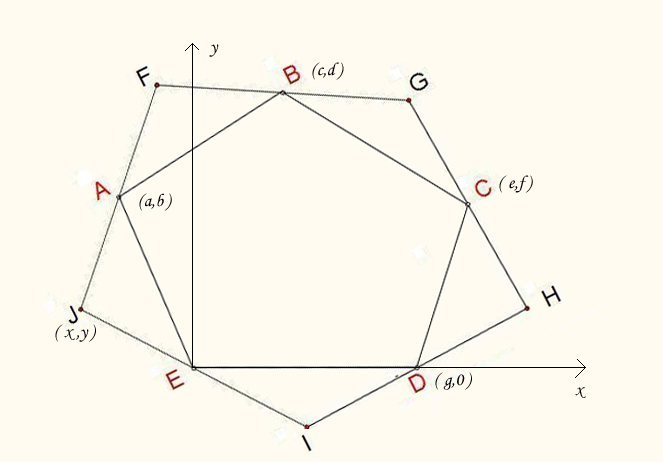
BoJone是习惯性地把这些题目用坐标来分析，如下图，把已知的五个顶点放到坐标系中，DE边为x轴，E为原点，并且设5个点分别为A(a,b);B(c,d);C(e,f);D(g,0);E(0,0)

五边形问题-坐标图

五边形问题-坐标图

倘若我们能够知道五边形FGHIJ任意一点，那么这个五边形就很容易做出来的。我们设法求出J点。设J点的坐标为(x,y)，根据J、A、F共线，JA=AF，可以得到F的坐标为(2a-x,2b-y)；同理，G点的坐标为(2c-2a+x,2d-2b+y)；H点的坐标为(2e-2c+2a-x,2f-2d+2b-y)；I点的坐标为(2g-2e+2c-2a+x,-2f+2d-2b+y)；J点的坐标为(-2g+2e-2c+2a-x,2f-2d+2b-y)。

别忘了我们一开始设J=(x,y)，所以应该有：
-2g+2e-2c+2a-x=x
2f-2d+2b-y=y

可以算出x=-g+e-c+a，y=f-d+b .天哪！作这个量实在太简单了吧！！只要把已知到的几个量加加减减就行了。

下面简单地说一下作法：

1、选择ED为x轴，E为原点，作出y轴
2、在y轴上分别画出AE、BE、CE的投影。
3、在y轴作出等于“AE、CE两投影之和减去BE的投影”的线段
4、在x轴上分别画出AE、BE、CE的投影
5、在x轴作出等于“AE、CE两投影之和减去BE的投影与ED之和”的线段
6、以3、5两步确定的坐标，作出点J
6、作直线JA，并截取AF=JA；接下来的步骤类似....直到把五边形画出来！

转载到请包括本文地址：https://kexue.fm/archives/753

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jul. 25, 2010). 《已知中心五边形，作五边形 》[Blog post]. Retrieved from https://kexue.fm/archives/753

@online{kexuefm-753,
        title={已知中心五边形，作五边形},
        author={苏剑林},
        year={2010},
        month={Jul},
        url={\url{https://kexue.fm/archives/753}},
}