科学空间|Scientific Spaces

这篇文章我们继续来闭门造车，分享一下笔者最近对多模态学习的一些新理解。

在前文《“闭门造车”之多模态思路浅谈（一）：无损输入》中，我们强调了无损输入对于理想的多模型模态的重要性。如果这个观点成立，那么当前基于VQ-VAE、VQ-GAN等将图像离散化的主流思路就存在能力瓶颈，因为只需要简单计算一下信息熵就可以表明离散化必然会有严重的信息损失，所以更有前景或者说更长远的方案应该是输入连续型特征，比如直接将图像的原始像素特征Patchify后输入到模型中。

然而，连续型输入对于图像理解自然简单，但对图像生成来说则引入了额外的困难，因为非离散化无法直接套用文本的自回归框架，多少都要加入一些新内容如扩散，这就引出了本文的主题——如何进行多模态的自回归学习与生成。当然，非离散化只是表面的困难，更艰巨的部份还在后头...

无损含义

首先我们再来明确一下无损的含义。无损并不是指整个计算过程中一丁点损失都不能有，这不现实，也不符合我们所理解的深度学习的要义——在2015年的文章《闲聊：神经网络与深度学习》我们就提到过，深度学习成功的关键是信息损失。所以，这里无损的含义很简单，单纯是希望作为模型的输入来说尽可能无损。

点击阅读全文...

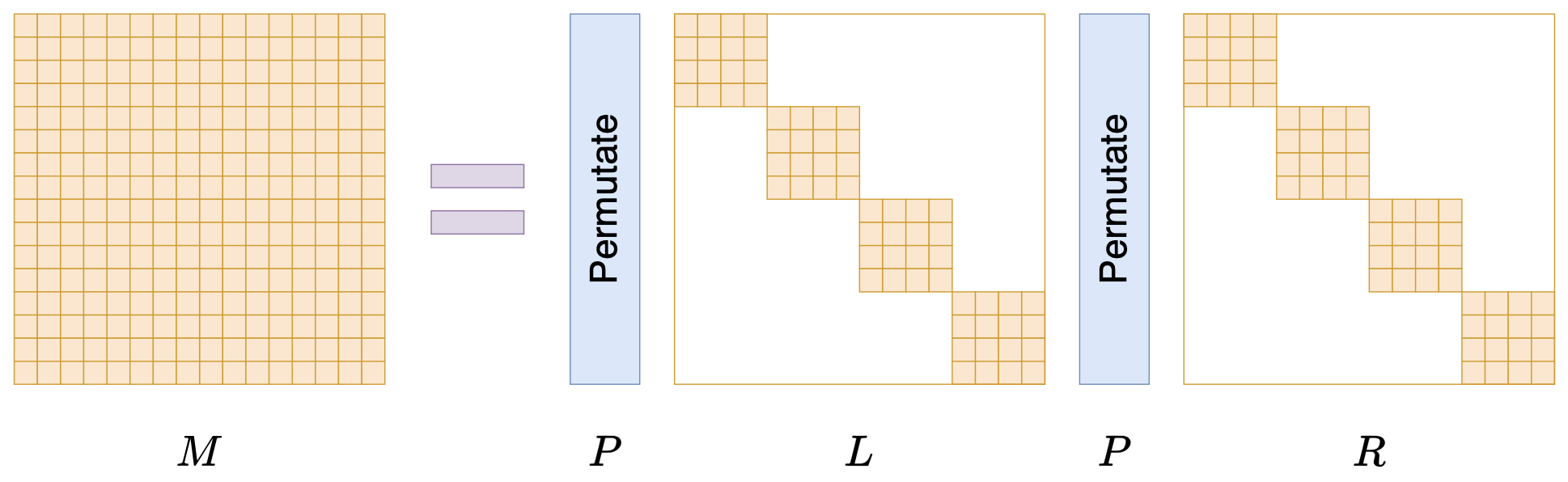
在矩阵压缩这个问题上，我们通常有两个策略可以选择，分别是低秩化和稀疏化。低秩化通过寻找矩阵的低秩近似来减少矩阵尺寸，而稀疏化则是通过减少矩阵中的非零元素来降低矩阵的复杂性。如果说SVD是奔着矩阵的低秩近似去的，那么相应地寻找矩阵稀疏近似的算法又是什么呢？

接下来我们要学习的是论文《Monarch: Expressive Structured Matrices for Efficient and Accurate Training》，它为上述问题给出了一个答案——“Monarch矩阵”，这是一簇能够分解为若干置换矩阵与稀疏矩阵乘积的矩阵，同时具备计算高效且表达能力强的特点，论文还讨论了如何求一般矩阵的Monarch近似，以及利用Monarch矩阵参数化LLM来提高LLM速度等内容。

Monarch矩阵形式M=PLPR

值得指出的是，该论文的作者也正是著名的Flash Attention的作者Tri Dao，其工作几乎都在致力于改进LLM的性能，这篇Monarch也是他主页上特意展示的几篇论文之一，单从这一点看就非常值得学习一番。

点击阅读全文...

可能很多读者跟笔者一样，对矩阵的低秩近似有种熟悉而又陌生的感觉。熟悉是因为，低秩近似的概念和意义都不难理解，加之目前诸如LoRA等基于低秩近似的微调技术遍地开花，让低秩近似的概念在耳濡目染间就已经深入人心；然而，低秩近似所覆盖的内容非常广，在低秩近似相关的论文中时常能看到一些不熟悉但又让我们叹为观止的新技巧，这就导致了一种似懂非懂的陌生感。

因此，在这个系列文章中，笔者将试图系统梳理一下矩阵低秩近似相关的理论内容，以补全对低秩近似的了解。而在第一篇文章中，我们主要介绍低秩近似系列中相对简单的一个概念——伪逆。

优化视角

伪逆（Pseudo Inverse），也称“广义逆（Generalized Inverse）”，顾名思义就是“广义的逆矩阵”，它实际上是“逆矩阵”的概念对于不可逆矩阵的推广。

点击阅读全文...

随着多模态LLM的方兴未艾，VQ（Vector Quantization）的地位也“水涨船高”，它可以作为视觉乃至任意模态的Tokenizer，将多模态数据统一到自回归生成框架中。遗憾的是，自VQ-VAE首次提出VQ以来，其理论并没有显著进步，像编码表的坍缩或利用率低等问题至今仍亟待解决，取而代之的是FSQ等替代方案被提出，成为了VQ有力的“竞争对手”。

然而，FSQ并不能在任何场景下都替代VQ，所以VQ本身的改进依然是有价值的。近日笔者读到了《Restructuring Vector Quantization with the Rotation Trick》，它提出了一种旋转技巧，声称能改善VQ的一系列问题，本文就让我们一起来品鉴一下。

回顾

早在五年前的博文《VQ-VAE的简明介绍：量子化自编码器》中我们就介绍过了VQ-VAE，后来在《简单得令人尴尬的FSQ：“四舍五入”超越了VQ-VAE》介绍FSQ的时候，也再次仔细地温习了VQ-VAE，还不了解的读者可以先阅读这两篇文章。

点击阅读全文...

不知道还有没有读者对这个系列有印象？这个系列取名“细水长flow”，主要介绍flow模型的相关工作，起因是当年（2018年）OpenAI发布了一个新的流模型Glow，在以GAN为主流的当时来说着实让人惊艳了一番。但惊艳归惊艳，事实上在相当长的时间内，Glow及后期的一些改进在生成效果方面都是比不上GAN的，更不用说现在主流的扩散模型了。

不过局面可能要改变了，上个月的论文《Normalizing Flows are Capable Generative Models》提出了新的流模型TARFLOW，它在几乎在所有的生成任务效果上都逼近了当前SOTA，可谓是流模型的“满血”回归。

TARFLOW的生成效果

点击阅读全文...

这篇文章我们再次聚焦于扩散模型的采样加速。众所周知，扩散模型的采样加速主要有两种思路，一是开发更高效的求解器，二是事后蒸馏。然而，据笔者观察，除了上两篇文章介绍过的SiD外，这两种方案都鲜有能将生成步数降低到一步的结果。虽然SiD能做到单步生成，但它需要额外的蒸馏成本，并且蒸馏过程中用到了类似GAN的交替训练过程，总让人感觉差点意思。

本文要介绍的是《One Step Diffusion via Shortcut Models》，其突破性思想是将生成步长也作为扩散模型的条件输入，然后往训练目标中加入了一个直观的正则项，这样就能直接稳定训练出可以单步生成模型，可谓简单有效的经典之作。

ODE扩散

原论文的结论是基于ODE式扩散模型的，而对于ODE式扩散的理论基础，我们在本系列的（六）、（十二）、（十四）、（十五）、（十七）等博客中已经多次介绍，其中最简单的一种理解方式大概是（十七）中的ReFlow视角，下面我们简单重复一下。

点击阅读全文...

证明下列级数发散或者收敛：
(1) $\sum_{x = 1}^\infty \frac{1}{x} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ...$
(2) $\sum_{x = 1}^\infty \frac{1}{x^2} = 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + ...$

一眼看上去，由于$1/x,1/{x^2}$都会趋向零，所以它们应该是收敛的。真的是这样吗？

点击阅读全文...

$\sum_{i=0}^{\infty} a_i x^i=a_0+a_1 x+a_2 x^2+a_3 x^3+...$
最近为了数学竞赛，我研究了有关数列和排列组合的相关问题。由于我讨厌为某个问题而设计专门的技巧，所以我偏爱通用的方法，哪怕过程相对麻烦。因此，我对数学归纳法（递推法）和生成函数法情有独钟。前者只需要列出问题的递归关系，而不用具体分析，最终把问题转移到解函数方程上来。后者则巧妙地把数列${a_n}$与幂级数$\sum_{i=0}^{\infty} a_i x^i$一一对应，巧妙地通过代数运算或微积分运算等得到结果。这里我们不用考虑该级数的敛散性，只需要知道它对应着哪一个“母函数”（母函数展开泰勒级数后得到了级数$\sum_{i=0}^{\infty} a_i x^i$）。显然，这两种方法的最终，都是把问题归结为代数问题。

点击阅读全文...