细水长flow之RealNVP与Glow:流模型的传承与升华
By 苏剑林 | 2018-08-26 | 457504位读者 |话在开头 #
上一篇文章《细水长flow之NICE:流模型的基本概念与实现》中,我们介绍了flow模型中的一个开山之作:NICE模型。从NICE模型中,我们能知道flow模型的基本概念和基本思想,最后笔者还给出了Keras中的NICE实现。
本文我们来关心NICE的升级版:RealNVP和Glow。
精巧的flow #
不得不说,flow模型是一个在设计上非常精巧的模型。总的来看,flow就是想办法得到一个encoder将输入$\boldsymbol{x}$编码为隐变量$\boldsymbol{z}$,并且使得$\boldsymbol{z}$服从标准正态分布。得益于flow模型的精巧设计,这个encoder是可逆的,从而我们可以立马从encoder写出相应的decoder(生成器)出来,因此,只要encoder训练完成,我们就能同时得到decoder,完成生成模型的构建。
为了完成这个构思,不仅仅要使得模型可逆,还要使得对应的雅可比行列式容易计算,为此,NICE提出了加性耦合层,通过多个加性耦合层的堆叠,使得模型既具有强大的拟合能力,又具有单位雅可比行列式。就这样,一种不同于VAE和GAN的生成模型——flow模型就这样出来了,它通过巧妙的构造,让我们能直接去拟合概率分布本身。
待探索的空间 #
NICE提供了flow模型这样一种新的思路,并完成了简单的实验,但它同时也留下了更多的未知的空间。flow模型构思巧妙,相比之下,NICE的实验则显得过于粗糙:只是简单地堆叠了全连接层,并没有给出诸如卷积层的用法,论文虽然做了多个实验,但事实上真正成功的实验只有MNIST,说服力不够。
因此,flow模型还需要进一步挖掘,才能在生成模型领域更加出众。这些拓展,由它的“继承者”RealNVP和Glow模型完成了,可以说,它们的工作使得flow模型大放异彩,成为生成模型领域的佼佼者。
RealNVP #
这部分我们来介绍RealNVP模型,它是NICE的改进,来自论文《Density estimation using Real NVP》。它一般化了耦合层,并成功地在耦合模型中引入了卷积层,使得可以更好地处理图像问题。更进一步地,它还提出了多尺度层的设计,这能够降低计算量,通过还提供了强大的正则效果,使得生成质量得到提升。至此,flow模型的一般框架开始形成。
后面的Glow模型基本上沿用了RealNVP的框架,只是对部分内容进行了修改(比如引入了可逆1x1卷积来代替排序层)。不过值得一提的是,Glow简化了RealNVP的结构,表明RealNVP中某些比较复杂的设计是没有必要的。因此本文在介绍RealNVP和Glow时,并没有严格区分它们,而只是突出它们的主要贡献。
仿射耦合层 #
其实NICE和RealNVP的第一作者都是Laurent Dinh,他是Bengio的博士生,他对flow模型的追求和完善十分让我钦佩。在第一篇NICE中,他提出了加性耦合层,事实上也提到了乘性耦合层,只不过没有用上;而在RealNVP,加性和乘性耦合层结合在一起,成为一个一般的“仿射耦合层”。
$$\begin{aligned}&\boldsymbol{h}_{1} = \boldsymbol{x}_{1}\\
&\boldsymbol{h}_{2} = \boldsymbol{s}(\boldsymbol{x}_{1})\otimes\boldsymbol{x}_{2} + \boldsymbol{t}(\boldsymbol{x}_{1})\end{aligned}\tag{1}$$
这里的$\boldsymbol{s},\boldsymbol{t}$都是$\boldsymbol{x}_1$的向量函数,形式上第二个式子对应于$\boldsymbol{x}_2$的一个仿射变换,因此称为“仿射耦合层”。
仿射耦合的雅可比矩阵依然是一个三角阵,但对角线不全为1,用分块矩阵表示为
$$\left[\frac{\partial \boldsymbol{h}}{\partial \boldsymbol{x}}\right]=\begin{pmatrix}\mathbb{I}_d & \mathbb{O} \\
\left[\frac{\partial \boldsymbol{s}}{\partial \boldsymbol{x}_1}\otimes \boldsymbol{x}_2+\frac{\partial \boldsymbol{t}}{\partial \boldsymbol{x}_1}\right] & \boldsymbol{s}\end{pmatrix}\tag{2}$$
很明显,它的行列式就是$\boldsymbol{s}$各个元素之积。为了保证可逆性,一般我们约束$\boldsymbol{s}$各个元素均大于零,所以一般情况下,我们都是直接用神经网络建模输出$\log \boldsymbol{s}$,然后取指数形式$e^{\log \boldsymbol{s}}$。
注:从仿射层大概就可以知道RealNVP的名称来源了,它的全称为“real-valued non-volume preserving”,强行翻译为“实值非体积保持”。相对于加性耦合层的行列式为1,RealNVP的雅可比行列式不再恒等于1,而我们知道行列式的几何意义就是体积(请参考《〈新理解矩阵5〉:体积=行列式》),所以行列式等于1就意味着体积没有变化,而仿射耦合层的行列式不等于1就意味着体积有所变化,所谓“非体积保持”。
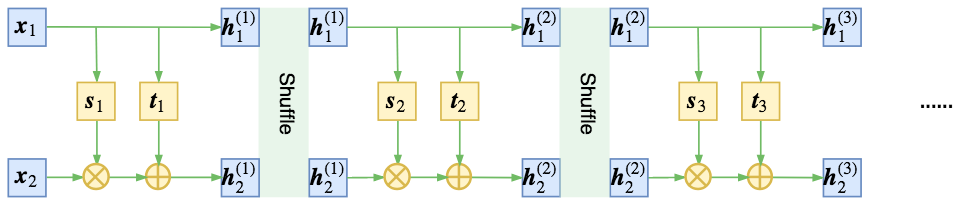
随机打乱维度 #
在NICE中,作者通过交错的方式来混合信息流(这也理论等价于直接反转原来的向量),如下图(对应地,这里已经换为本文的仿射耦合层图示):
而RealNVP发现,通过随机的方式将向量打乱,可以使信息混合得更加充分,最终的loss可以更低,如图
这里的随机打乱,就是指将每一步flow输出的两个向量$\boldsymbol{h}_1, \boldsymbol{h}_2$拼接成一个向量$\boldsymbol{h}$,然后将这个向量重新随机排序。
引入卷积层 #
RealNVP中给出了在flow模型中合理使用卷积神经网络的方案,这使得我们可以更好地处理图像问题,并且减少参数量,还可以更充分发挥模型的并行性能。
注意,不是任意情况下套用卷积都是合理的,用卷积的前提是输入(在空间维度)具有局部相关性。图像本身是具有局部相关性的,因为相邻之间的像素是有一定关联的,因此一般的图像模型都可以使用卷积。但是我们注意flow中的两个操作:1、将输入分割为两部分$\boldsymbol{x}_1,\boldsymbol{x}_2$,然后输入到耦合层中,而模型$\boldsymbol{s},\boldsymbol{t}$事实上只对$\boldsymbol{x}_1$进行处理;2、特征输入耦合层之前,要随机打乱原来特征的各个维度(相当于乱序的特征)。这两个操作都会破坏局部相关性,比如分割操作有可能割裂原来相邻的像素,随机打乱也可能将原来相邻的两个像素分割得很远。
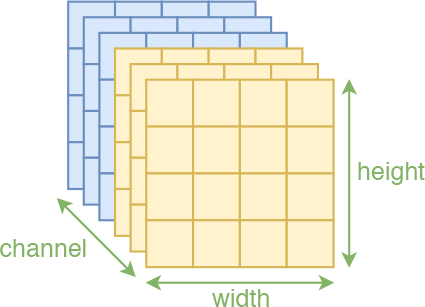
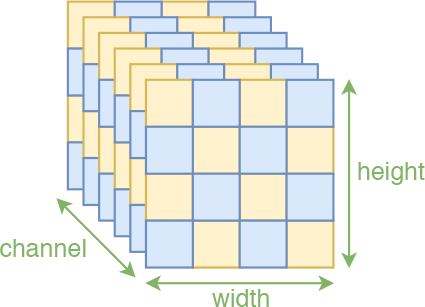
所以,如果还要坚持使用卷积,就要想办法保留这种空间的局部相关性。我们知道,一幅图像有三个轴:高度(height)、宽度(width)、通道(channel),前两个属于空间轴,显然具有局部相关性,因此能“搞”的就只有“通道”轴。为此,RealNVP约定分割和打乱操作,都只对“通道”轴执行。也就是说,沿着通道将输入分割为$\boldsymbol{x}_1,\boldsymbol{x}_2$后,$\boldsymbol{x}_1$还是具有局部相关性的,还有沿着通道按着同一方式打乱整体后,空间部分的相关性依然得到保留,因此在模型$\boldsymbol{s},\boldsymbol{t}$中就可以使用卷积了。
注:在RealNVP中,将输入分割为两部分的操作称为mask,因为这等价于用0/1来区别标注原始输入。除了前面说的通过通道轴对半分的mask外,RealNVP事实上还引入了一种空间轴上的交错mask,如上图的右边,这种mask称为棋盘式mask(格式像国际象棋的棋盘)。这种特殊的分割也保留了空间局部相关性,原论文中是两种mask方式交替使用的,但这种棋盘式mask相对复杂,也没有什么特别明显的提升,所以在Glow中已经被抛弃。
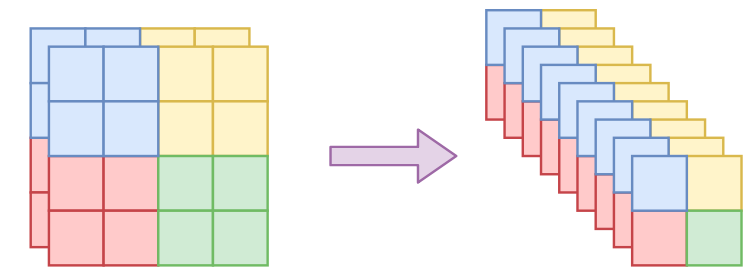
不过想想就会发现有问题。一般的图像通道轴就只有三维,像MNIST这种灰度图还只有一维,怎么分割成两半?又怎么随机打乱?为了解决这个问题,RealNVP引入了称为squeeze的操作,来让通道轴具有更高的维度。其思想很简单:直接reshape,但reshape时局部地进行。具体来说,假设原来图像为$h\times w\times c$大小,前两个轴是空间维度,然后沿着空间维度分为一个个$2\times 2\times c$的块(这个2可以自定义),然后将每个块直接reshape为$1\times 1\times 4c$,也就是说最后变成了$h/2 \times w/2 \times 4c$。
有了squeeze这个操作,我们就可以增加通道轴的维数,但依然保留局部相关性,从而我们前面说的所有事情都可以进行下去了,所以squeeze成为flow模型在图像应用中的必备操作。
多尺度结构 #
除了成功地引入卷积层外,RealNVP的另一重要进展是加入了多尺度结构。跟卷积层一样,这也是一个既减少了模型复杂度、又提升了结果的策略。
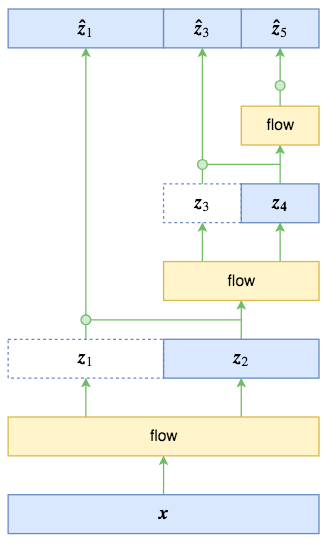
多尺度结构其实并不复杂,如图所示。原始输入经过第一步flow运算(“flow运算”指的是多个仿射耦合层的复合)后,输出跟输入的大小一样,这时候将输入对半分开两半$\boldsymbol{z}_1,\boldsymbol{z}_2$(自然也是沿着通道轴),其中$\boldsymbol{z}_1$直接输出,而只将$\boldsymbol{z}_2$送入到下一步flow运算,后面的依此类推。比如图中的特例,最终的输出由$\boldsymbol{z}_1,\boldsymbol{z}_3,\boldsymbol{z}_5$组成,总大小跟输入一样。
多尺度结构有点“分形”的味道,原论文说它启发于VGG。每一步的多尺度操作直接将数据尺寸减少到原来的一半,显然是非常可观的。但有一个很重要的细节,在RealNVP和Glow的论文中都没有提到,我是看了源码才明白的,那就是最终的输出$[\boldsymbol{z}_1,\boldsymbol{z}_3,\boldsymbol{z}_5]$的先验分布应该怎么取?按照flow模型的通用假设,直接设为一个标准正态分布?
事实上,作为不同位置的多尺度输出,$\boldsymbol{z}_1,\boldsymbol{z}_3,\boldsymbol{z}_5$的地位是不对等的,而如果直接设一个总体的标准正态分布,那就是强行将它们对等起来,这是不合理的。最好的方案,应该是写出条件概率公式
$$p(\boldsymbol{z}_1,\boldsymbol{z}_3,\boldsymbol{z}_5)=p(\boldsymbol{z}_1|\boldsymbol{z}_3,\boldsymbol{z}_5)p(\boldsymbol{z}_3|\boldsymbol{z}_5)p(\boldsymbol{z}_5)\tag{3}$$
由于$\boldsymbol{z}_3,\boldsymbol{z}_5$是由$\boldsymbol{z}_2$完全决定的,$\boldsymbol{z}_5$也是由$\boldsymbol{z}_4$完全决定的,因此条件部分可以改为
$$p(\boldsymbol{z}_1,\boldsymbol{z}_3,\boldsymbol{z}_5)=p(\boldsymbol{z}_1|\boldsymbol{z}_2)p(\boldsymbol{z}_3|\boldsymbol{z}_4)p(\boldsymbol{z}_5)\tag{4}$$
RealNVP和Glow假设右端三个概率分布都是正态分布,其中$p(\boldsymbol{z}_1|\boldsymbol{z}_2)$的均值方差由$\boldsymbol{z}_2$算出来(可以直接通过卷积运算,这有点像VAE),$p(\boldsymbol{z}_3|\boldsymbol{z}_4)$的均值方差由$\boldsymbol{z}_4$算出来,$p(\boldsymbol{z}_5)$的均值方差直接学习出来。
显然这样的假设会比简单认为它们都是标准正态分布要有效得多。我们还可以换一种表述方法:上述的先验假设相当于做了如下的变量代换
$$\boldsymbol{\hat{z}}_1=\frac{\boldsymbol{z}_1 - \boldsymbol{\mu}(\boldsymbol{z}_2)}{\boldsymbol{\sigma}(\boldsymbol{z}_2)},\quad \boldsymbol{\hat{z}}_3=\frac{\boldsymbol{z}_3 - \boldsymbol{\mu}(\boldsymbol{z}_4)}{\boldsymbol{\sigma}(\boldsymbol{z}_4)},\quad \boldsymbol{\hat{z}}_5=\frac{\boldsymbol{z}_5 - \boldsymbol{\mu}}{\boldsymbol{\sigma}}\tag{5}$$
然后认为$[\boldsymbol{\hat{z}}_1,\boldsymbol{\hat{z}}_3,\boldsymbol{\hat{z}}_5]$服从标准正态分布。同NICE的尺度变换层一样,这三个变换都会导致一个非1的雅可比行列式,也就是要往loss中加入形如$\sum\limits_{i=1}^D\log \boldsymbol{\sigma}_i$的这一项。
咋看之下多尺度结构就是为了降低运算量,但并不是那么简单。由于flow模型的可逆性,输入输出维度一样,事实上这会存在非常严重的维度浪费问题,这往往要求我们需要用足够复杂的网络去缓解这个维度浪费。多尺度结构相当于抛弃了$p(\boldsymbol{z})$是标准正态分布的直接假设,而采用了一个组合式的条件分布,这样尽管输入输出的总维度依然一样,但是不同层次的输出地位已经不对等了,模型可以通过控制每个条件分布的方差来抑制维度浪费问题(极端情况下,方差为0,那么高斯分布坍缩为狄拉克分布,维度就降低1),条件分布相比于独立分布具有更大的灵活性。而如果单纯从loss的角度看,多尺度结构为模型提供了一个强有力的正则项(相当于多层图像分类模型中的多条直连边)。
Glow #
整体来看,Glow模型在RealNVP的基础上引入了1x1可逆卷积来代替前面说的打乱通道轴的操作,并且对RealNVP的原始模型做了简化和规范,使得它更易于理解和使用。
Glow论文:https://papers.cool/arxiv/1807.03039
Glow博客:https://blog.openai.com/glow/
Glow源码:https://github.com/openai/glow
可逆1x1卷积 #
这部分介绍Glow的主要改进工作:可逆1x1卷积。
置换矩阵 #
可逆1x1卷积源于我们对置换操作的一般化。我们知道,在flow模型中,一步很重要的操作就是将各个维度重新排列,NICE是简单反转,而RealNVP则是随机打乱。不管是哪一种,都对应着向量的置换操作。
事实上,对向量的置换操作,可以用矩阵乘法来描述,比如原来向量是$[1, 2, 3, 4]$,分别交换第一、二和第三、四两个数,得到$[2, 1, 4, 3]$,这个操作可以用矩阵乘法来描述:
$$\begin{pmatrix}2 \\ 1 \\ 4 \\ 3\end{pmatrix} = \begin{pmatrix}0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0\end{pmatrix} \begin{pmatrix}1 \\ 2 \\ 3 \\ 4\end{pmatrix}\tag{6}$$
其中右端第一项是“由单位矩阵不断交换两行或两列最终得到的矩阵”,称为置换矩阵。
一般化置换 #
既然这样,那很自然的想法就是:为什么不将置换矩阵换成一般的可训练的参数矩阵呢?所谓1x1可逆卷积,就是这个想法的结果。
注意,我们一开始提出flow模型的思路时就已经明确指出,flow模型中的变换要满足两个条件:一是可逆,二是雅可比行列式容易计算。如果直接写出变换
$$\boldsymbol{h}=\boldsymbol{x}\boldsymbol{W}\tag{7}$$
那么它就只是一个普通的没有bias的全连接层,并不能保证满足这两个条件。为此,我们要做一些准备工作。首先,我们让$\boldsymbol{h}$和$\boldsymbol{x}$的维度一样,也就是说$\boldsymbol{W}$是一个方阵,这是最基本的设置;其次,由于这只是一个线性变换,因此它的雅可比矩阵就是$\left[\frac{\partial \boldsymbol{h}}{\partial \boldsymbol{x}} \right]=\boldsymbol{W}$,所以它的行列式就是$\det \boldsymbol{W}$,因此我们需要把$-\log |\det \boldsymbol{W}|$这一项加入到loss中;最后,初始化时为了保证$\boldsymbol{W}$的可逆性,一般使用“随机正交矩阵”初始化。
利用LU分解 #
以上做法只是一个很基本的解决方案,我们知道,算矩阵的行列式运算量特别大,还容易溢出。而Glow给出了一个非常巧妙的解决方案:LU分解的逆运用。具体来说,是因为任意矩阵都可以分解为
$$\boldsymbol{W}=\boldsymbol{P}\boldsymbol{L}\boldsymbol{U}\tag{8}$$
其中$\boldsymbol{P}$是一个置换矩阵,也就是前面说的shuffle的等价矩阵;$\boldsymbol{L}$是一个下三角阵,对角线元素全为1;$\boldsymbol{U}$是一个上三角阵。这种形式的分解称为LU分解。如果知道这种矩阵的表达形式,显然求雅可比行列式是很容易的,它等于
$$\log |\det \boldsymbol{W}| = \sum \log|\text{diag}(\boldsymbol{U})|\tag{9}$$
也就是$\boldsymbol{U}$的对角线元素的绝对值对数之和。既然任意矩阵都可以分解成$(8)$式,我们何不直接设$\boldsymbol{W}$的形式为$(8)$式?这样一来矩阵乘法计算量并没有明显提升,但求行列式的计算量大大降低,而且计算起来也更为容易。这就是Glow中给出的技巧:先随机生成一个正交矩阵,然后做LU分解,得到$\boldsymbol{P},\boldsymbol{L},\boldsymbol{U}$,固定$\boldsymbol{P}$,也固定$\boldsymbol{U}$的对角线的正负号,然后约束$\boldsymbol{L}$为对角线全1的下三角阵,$\boldsymbol{U}$为上三角阵,优化训练$\boldsymbol{L},\boldsymbol{U}$的其余参数。
结果分析 #
上面的描述只是基于全连接的。如果用到图像中,那么就要在每个通道向量上施行同样的运算,这等价于1x1的卷积,这就是所谓的可逆1x1卷积的来源。事实上我觉得这个名字起得不大好,它本质上就是共享权重的、可逆的全连接层,单说1x1卷积,就把它局限在图像中了,不够一般化。
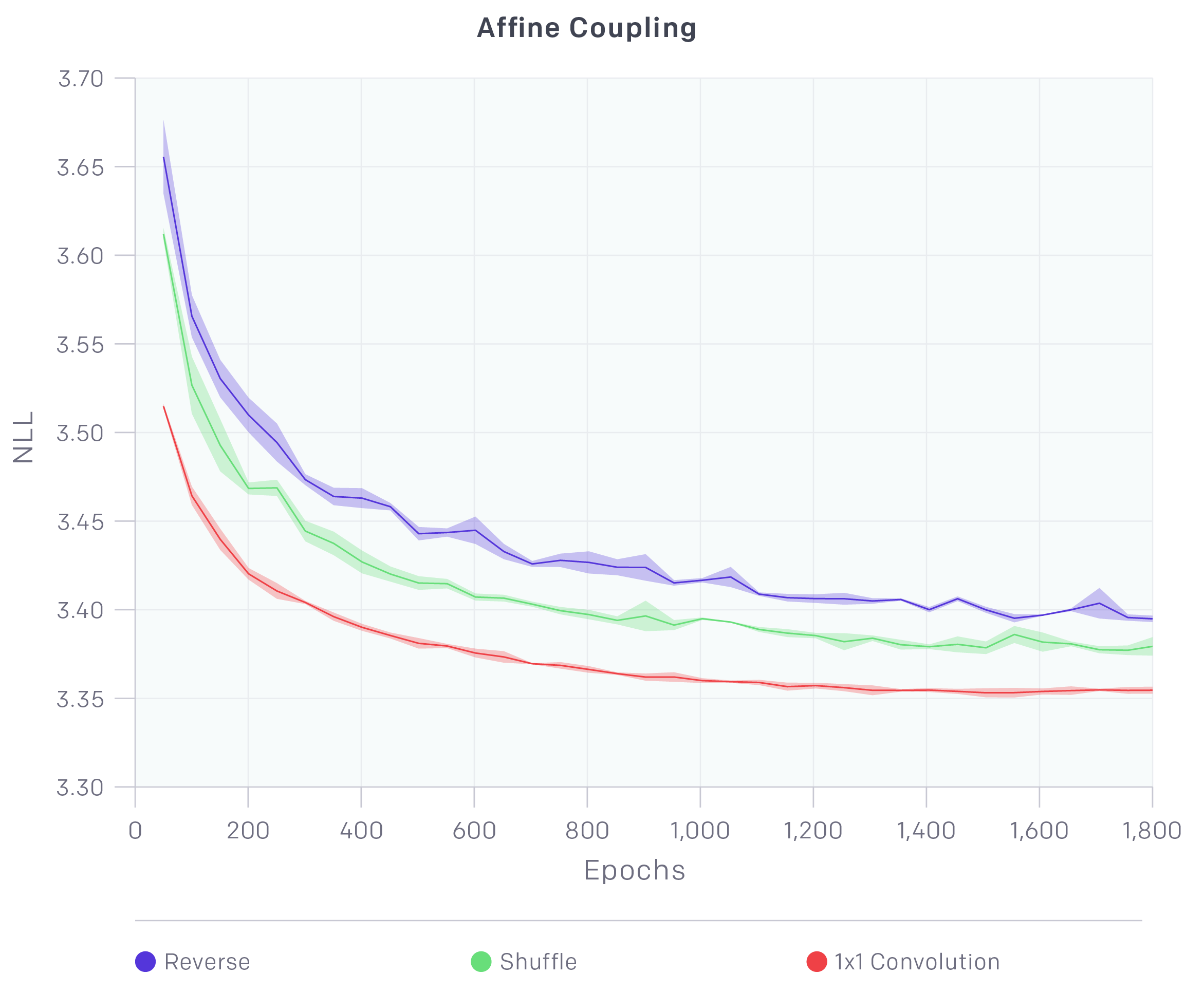
Glow的论文做了对比实验,表明相比于直接反转,shuffle能达到更低的loss,而相比shuffle,可逆1x1卷积能达到更低的loss。我自己的实验也表明了这一点。
不过要指出的是:可逆1x1卷积虽然能降低loss,但是有一些要注意的问题。第一,loss的降低不代表生成质量的提高,比如A模型用了shuffle,训练200个epoch训练到loss=-50000,B模型用了可逆卷积,训练150个epoch就训练到loss=-55000,那么通常来说在当前情况下B模型的效果还不如A(假设两者都还没有达到最优)。事实上可逆1x1卷积只能保证大家都训练到最优的情况下,B模型会更优。第二,在我自己的简单实验中貌似发现,用可逆1x1卷积达到饱和所需要的epoch数,要远多于简单用shuffle的epoch数。
Actnorm #
RealNVP中用到了BN层,而Glow中提出了名为Actnorm的层来取代BN。不过,所谓Actnorm层事实上只不过是NICE中的尺度变换层的一般化,也就是$(5)$式提到的缩放平移变换
$$\boldsymbol{\hat{z}}=\frac{\boldsymbol{z} - \boldsymbol{\mu}}{\boldsymbol{\sigma}}\tag{10}$$
其中$\boldsymbol{\mu},\boldsymbol{\sigma}$都是训练参数。Glow在论文中提出的创新点是用初始的batch的均值和方差去初始化$\boldsymbol{\mu},\boldsymbol{\sigma}$这两个参数,但事实上所提供的源码并没有做到这一点,纯粹是零初始化。
所以,这一点是需要批评的,纯粹将旧概念换了个新名字罢了。当然,批评的是OpenAI在Glow中乱造新概念,而不是这个层的效果。缩放平移的加入,确实有助于更好地训练模型。而且,由于Actnorm的存在,仿射耦合层的尺度变换已经显得不那么重要了。我们看到,相比于加性耦合层,仿射耦合层多了一个尺度变换层,从而计算量翻了一倍。但事实上相比加性耦合,仿射耦合效果的提升并不高(尤其是加入了Actnorm后),所以要训练大型的模型,为了节省资源,一般都只用加性耦合,比如Glow训练256x256的高清人脸生成模型,就只用到了加性耦合。
源码分析 #
事实上Glow已经没有什么可以特别解读的了。但是Glow整体的模型比较规范,我们可以逐步分解一下Glow的模型结构,为我们自己搭建类似的模型提供参考。这部分内容源自我对Glow源码的阅读,主要以示意图的方式给出。
模型总图 #
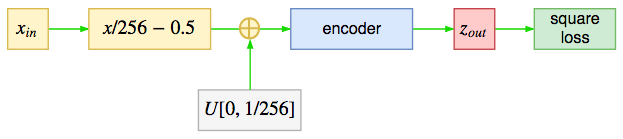
整体来看,glow模型并不复杂,就是在输入加入一定量的噪声,然后输入到一个encoder中,最终用“输出的平均平方和”作为损失函数(可以将模型中产生的对数雅可比行列式视为正则项),注意,loss不是“平方平均误差(MSE)”,而仅仅是输出的平方和,也就是不用减去输入。
encoder #
下面对总图中的encoder进行分解,大概流程为
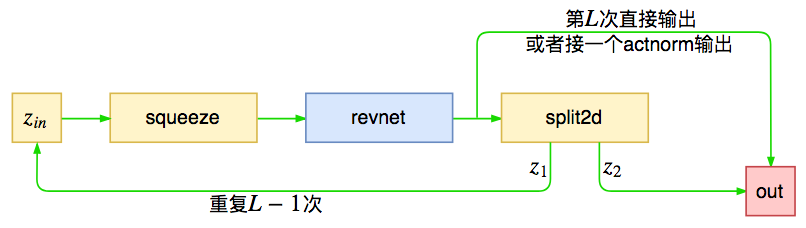
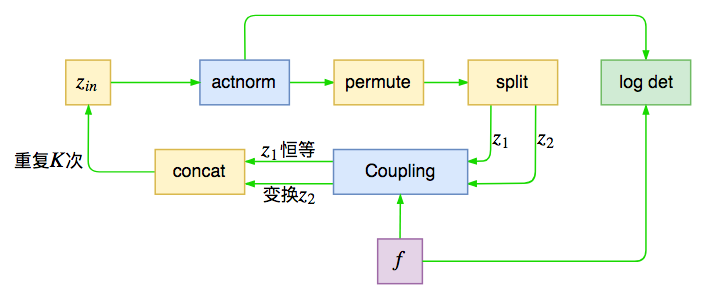
encoder由$L$个模块组成,这些模块在源码中被命名为revnet,每个模块的作用是对输入进行运算,然后将输出对半分为两份,一部分传入下一个模块,一部分直接输出,这就是前面说的多尺度结构。Glow源码中默认$L=3$,但对于256x256的人脸生成则用到$L=6$。
revnet #
现在来进一步拆解encoder,其中revnet部分为
其实它就是前面所说的单步flow运算,在输入之前进行尺度变换,然后打乱轴,并且进行分割,接着输入到耦合层中。如此训练$K$次,这里的$K$称为“深度”,Glow中默认是32。其中actnorm和仿射耦合层会带来非1的雅可比行列式,也就是会改动loss,在图上也已注明。
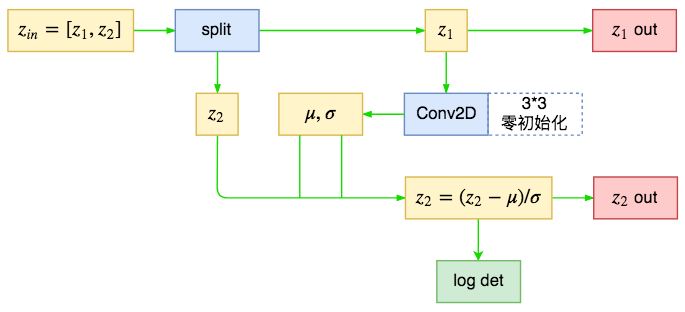
split2d #
Glow中的定义的split2d不是简单的分割,而是混合了对分割后的变换运算,也就是前面所提到的多尺度输出的先验分布选择。
对比$(5)$和$(10)$,我们可以发现条件先验分布与Actnorm的区别仅仅是缩放平移量的来源,Actnorm的缩放平移参数是直接优化而来,而先验分布这里的缩放平移量是由另一部分通过某个模型计算而来,事实上我们可以认为这种一种条件式Actnorm(Cond Actnorm)。
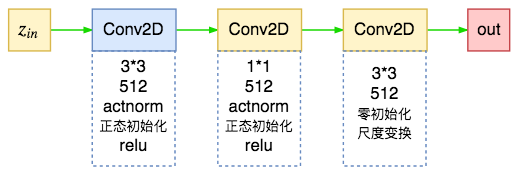
f #
最后是Glow中的耦合层的模型(放射耦合层的$\boldsymbol{s},\boldsymbol{t}$),源码中直接命名为f,它用了三层relu卷积:
其中最后一层使用零初始化,这样就使得初始状态下输入输出一样,即初始状态为一个恒等变换,这有利于训练深层网络
复现 #
可以看到RealNVP其实已经做好了大部分工作,而Glow在RealNVP的基础上进行去芜存菁,并加入了自己的一些小修改(1x1可逆卷积)和规范。但不管怎么样,这是一个值得研究的模型。
Keras版本 #
官方开源的Glow是tensorflow版的。这么有意思的模型,怎么能少得了Keras版呢,先奉上笔者实现的Keras版:
https://github.com/bojone/flow/blob/master/glow.py
(已经pull request到Keras官方的examples,希望过几天能在Keras的github上看到它)
由于某些函数的限制,目前只支持tensorflow后端,我的测试环境包括:Keras 2.1.5 + tensorflow 1.2 和 Keras 2.2.0 + tensorflow 1.8,均在Python 2.7下测试。
效果测试 #
刚开始读到Glow时,我感到很兴奋,仿佛像发现了新大陆一样。经过一番学习后,我发现......Glow确实是一块新大陆,然而却非我等平民能轻松登上的。
让我们来看Glow的github上的两个issue:
《How many epochs will be take when training celeba?》
The samples we show in the paper are after about 4000 training epochs...《anyone reproduced the celeba-HQ results in the paper》
Yes we trained with 40 GPU's for about a week, but samples did start to look good after a couple of days...
我们看到256x256的高清人脸图像生成,需要训练4000个epoch,用40个GPU训练了一周,简单理解就是用1个GPU训练一年...(卒)
好吧,我还是放弃这可望而不可及的任务吧,我们还是简简单单玩个64x64,不,还是32x32的人脸生成,做个demo出来就是了。
感觉还可以吧,我用的是$L=3,K=6$,每个epoch要70s左右(GTX1070)。跑了150个epoch,这里的epoch跟通常概念的epoch不一样,我这里的一个epoch就是随机抽取的3.2万个样本,如果每次跑完完整的epoch,那么用时更久...同样的模型,顺手也跑了一下cifar10,跑了700个epoch,不过效果不大好。就是远看似乎还可以,近看啥都不是的那种~
当然,其实cifar10虽然不大(32x32),但事实上生成cifar10可比生成人脸难多了(不管是哪种生成模型),我们就跳过吧。话说64x64的人脸,我也作死地尝试了一下,这时候用了$L=3,K=10$,跑了200个epoch(这时候每个epoch要6分钟了)。结果...
人脸是人脸了,不过看上去更像妖魔脸...(看来网络深度和epoch数都还不够,我也跑不下去了)。
退火参数也是比较重要的,将退火参数改为0.8后,同样的模型生成结果为
还有点扭曲,不过看起来好很多了。
艰难结束 #
好了,对RealNVP和Glow的介绍终于可以结束了。本着对Glow的兴趣,利用前后两篇文章把三个flow模型都捋了一遍,希望对读者有帮助。
总体来看,诸如Glow的flow模型整体确实很优美,但运算量还是偏大了,训练时间过长,不像一般的GAN那么友好。个人认为flow模型要在当前以GAN为主的生成模型领域中站稳脚步,还有比较长的路子要走,可谓任重而道远呀。
转载到请包括本文地址:https://kexue.fm/archives/5807
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Aug. 26, 2018). 《细水长flow之RealNVP与Glow:流模型的传承与升华 》[Blog post]. Retrieved from https://kexue.fm/archives/5807
@online{kexuefm-5807,
title={细水长flow之RealNVP与Glow:流模型的传承与升华},
author={苏剑林},
year={2018},
month={Aug},
url={\url{https://kexue.fm/archives/5807}},
}















May 24th, 2024
@Jiawen Wei|comment-24397
我大概理解你的情况可能类似VAE,每个样本对应有一个隐变量分布,即$p(z|x)$,你是不是想说将$p(z|x)$换成flow模型而不是简单的高斯分布?你要不参考一下我之前做的f-vae?https://kexue.fm/archives/5977
October 31st, 2024
苏老师您好,我有一个疑惑,我理解X分布的PDF可以由Z分布的PDF乘雅可比矩阵行列式得来,但是为什么计算损失函数是计算$L(\theta|X)$,而不是$L(\theta|Z)$呢?我们希望Z分布尽可能接近$N(0,1)$,那么直接假定Z为正态分布,最大化$L(\theta|Z)=\prod_{i=1}^N p(z)$,将每个$z_i$带入N(0,1)的PDF即可。
我产生这种疑问是因为:在原始的计算NLL(X)过程中,我得到$NLL=-(\sum_{n=1}^N logp(z)+logdet$时,我的数据归一化之后标准差std很小,所以actnorm里的$scale=1/std$非常大,而不管affine coupling里scale取exp(s)还是sigmoid(s+2),actnorm得到的logdet已经足够大了,因此整个loss是一个绝对值很大的负数,很快affine coupling中的net权重就率先变成nan了(我猜是因为Adam接受了负数损失的问题)。我知道NLL可以为负,但是损失通常为非负数。我尝试用sigmoid函数将actnorm中的s控制在[0,1],使其log为(-inf,0],但是这就不能将方差变为1了,我的模型也很快得到了-inf值。因此我也近乎黔驴技穷了。这个问题困扰了我很久,如果您能解答,感激不尽!
“我们希望Z分布尽可能接近$N(0,1)$,那么直接假定Z为正态分布,最大化$L(\theta|Z)=\prod_{i=1}^N p(z)$,将每个$z_i$带入N(0,1)的PDF即可。”这还用优化吗?
我们的目标是生成$\boldsymbol{x}$,或者说建模$\boldsymbol{x}$的分布,我们的数据也都是$\boldsymbol{x}$的。假设$\boldsymbol{z}$的分布尽可能接近标准正态分布,只能是以$\boldsymbol{z}$为标准正态分布出发来建立$p_{\boldsymbol{\theta}}(\boldsymbol{x})$,然后取最大$p_{\boldsymbol{\theta}}(\boldsymbol{x})$的似然。
March 13th, 2025
苏老师您好,请问glow模型训练后得到的效果能实现z(潜在向量)->x(图像)->z',然后z近似等于z'的效果吗?因为我最近在复现一篇利用glow模型的可逆性来实现图像隐写的文献,这个工作成功的前提就是潜在向量能够在数值上近似地重建。但是我用openAI开源的预训练模型得到的效果却是:z和z'天差地别,尽管它们decode生成的图像是100%相同的。考虑到encode的过程中引入了随机性,所以想问一下这个理论上能实现吗?
如果是这里的glow模型,那么z跟z'应该是100%相同的,glow模型encode的过程没有随机性。
December 5th, 2025
苏老师您好,我也想问一个问题:
我在哔站看过 19 年李宏毅老师讲 Glow 的视频,他提到了一句话,“1*1 卷积使用的矩阵我们用可逆的矩阵初始化,但是这个矩阵后续训练的时候就一定是可逆的吗?这部分应该怎么理解?”李老师说这部分原论文没有提,他自己也不是很清楚,苏老师您怎么看这个问题呢?
这个很好理解吧,因为flow模型的loss里边包含行列式负对数啊,如果不可逆,行列式为0,那么loss将是无穷大,所以loss会主动规避不可逆。