一道概率不等式:盯着它到显然成立为止!
By 苏剑林 | 2025-04-30 | 26690位读者 |前两天,QQ群里有群友抛出了一道不等式求证:
简短的题目,加上“easily”的提示,让人觉得这似乎是显然成立的结果,然而提问者却表示尝试了很久仍未果。那么实际情况如何呢?是否真的是显然成立呢?
初步尝试 #
题目等价于证
\begin{equation}\sum_{i=0}^j p^i \leq \sum_{i=0}^j \left(\log\frac{1}{1-p}\right)^i/i!,\qquad p\in[0, 1)\label{eq:q}\end{equation}
所给的提示是
\begin{equation}\log\frac{1}{1-p} = \sum_{i=1}^{\infty} \frac{p^i}{i} = p + \frac{p^2}{2} + \frac{p^3}{3} + \cdots \label{eq:log-1-p}\end{equation}
这个提示似乎在引导我们替换掉式$\eqref{eq:q}$右端的$\log\frac{1}{1-p}$,然后展开成$p$的幂级数来逐项对比。由于$\log\frac{1}{1-p}$的展开式系数全是正数,所以式$\eqref{eq:q}$展开成$p$的幂级数后每一项系数必然也都是正数,因此我们只要证明前$j$项系数都大于等于1。
思路看上去靠谱,然而将一个幂级数的$i$次幂重新展开为幂级数是一件非常繁琐的事情,所以实际上很难走通。笔者又另外尝试了一些思路,比如设$x=\log\frac{1}{1-p}$转为关于$x$的不等式来证,看上去也很有希望,但最终都被卡住,无法完整完成证明。
所以,初次尝试宣布失败。
泰勒硬刚 #
兜兜转转,回到原点。试了大半天,总感觉还是将式$\eqref{eq:q}$右端展开为幂级数的思路靠谱,但直接对式$\eqref{eq:log-1-p}$求幂走不通的话,我们只能回到泰勒展开的原始做法——求导。
简单起见,我们定义
\begin{equation}f_j(x) = \sum_{i=0}^j \frac{x^i}{i!}\end{equation}
原题就是证
\begin{equation}f_j(x) \geq \sum_{i=0}^j p^i,\qquad x = \log\frac{1}{1-p}\end{equation}
我们转化为证
\begin{equation}\left.\frac{d^k}{dp^k}f_j(x)\right|_{p=0} \,\,\geq\,\, \left\{\begin{aligned}&\, 1,\,\, k \leq j \\[5pt]
&\,0,\,\, k > j\end{aligned}\right.\end{equation}
留意到当$j \geq 0$时$f_j(0)=1$,当$j < 0$时我们定义$f_j(x)\equiv 0$,以及成立$f_j'(x)= f_{j-1}(x)$,于是我们有
\begin{gather}\frac{d}{dp}f_j(x) = f_{j-1}(x) \frac{1}{1-p} \\
\frac{d^2}{dp^2}f_j(x) = [f_{j-1}(x) + f_{j-2}(x)]\frac{1}{(1-p)^2} \\
\frac{d^3}{dp^3}f_j(x) = [2f_{j-1}(x) + 3f_{j-2}(x) + f_{j-3}(x)]\frac{1}{(1-p)^3} \\
\vdots \notag\\
\frac{d^k}{dp^k}f_j(x) = [\alpha_1 f_{j-1}(x) + \alpha_2 f_{j-2}(x) + \cdots + \alpha_k f_{j-k}(x)]\frac{1}{(1-p)^k} \\[8pt]
\frac{d^{k+1}}{dp^{k+1}}f_j(x) = \left[\begin{aligned}
\alpha_1 f_{j-2}(x) + \alpha_2 f_{j-3}(x) + \cdots + \alpha_k f_{j-k-1}(x) \\
+ k(\alpha_1 f_{j-1}(x) + \alpha_2 f_{j-2}(x) + \cdots + \alpha_k f_{j-k}(x))
\end{aligned}\right]\frac{1}{(1-p)^{k+1}}
\end{gather}
规律:$\frac{d^k}{dp^k}f_j(x)$是$f_{j-1}(x),f_{j-2}(x),\cdots,f_{j-k}(x)$的线性组合与$\frac{1}{(1-p)^k}$的乘积,注意其实我们只关心$\left.\frac{d^k}{dp^k}f_j(x)\right|_{p=0}$的值,上式代入$p=0$后就等于$f_{j-1}(x),f_{j-2}(x),\cdots,f_{j-k}(x)$中非零项的系数之和(注意$f_{j-1}(0),f_{j-2}(0),\cdots,f_{j-k}(0)$非1即0)。根据$f_j(x)$的求导规律,我们可以得出:当$k \leq j$时,有
\begin{equation}\left.\frac{d^k}{dp^k}f_j(x)\right|_{p=0} = k \times \left.\frac{d^{k-1}}{dp^{k-1}}f_j(x)\right|_{p=0}\end{equation}
所以$\left.\frac{d^k}{dp^k}f_j(x)\right|_{p=0} = k!$,那么根据泰勒展开式$p^k$项的系数为$k!/k!=1$;当$k > j$时,由于此时$f_{j-k}(0)=0$,所以$\left.\frac{d^k}{dp^k}f_j(x)\right|_{p=0} < k!$,所以$p^k$项的系数则小于1,但仍旧大于零,因此所证不等式成立。
显然易得 #
这样看来,原题目并不是像作者说的显然成立了?笔者开始也是这样认为的,直到另一位群友给出了一个极其简单的理解视角,才恍然大悟,这道题还真的是显然成立的!
这个视角充分体现了逆向思维,如下:
\begin{equation}\begin{aligned}
\sum_{i=0}^j \left(\log\frac{1}{1-p}\right)^i/i! =&\, \sum_{i=0}^{\infty} \left(\log\frac{1}{1-p}\right)^i/i! - \sum_{i=j+1}^{\infty} \left(\log\frac{1}{1-p}\right)^i/i! \\
=&\, \exp\left(\log\frac{1}{1-p}\right) - \sum_{i=j+1}^{\infty} \left(\log\frac{1}{1-p}\right)^i/i! \\
=&\, \frac{1}{1-p} - \sum_{i=j+1}^{\infty} \left(\log\frac{1}{1-p}\right)^i/i! \\
=&\, \sum_{i=1}^{\infty} p^i - \sum_{i=j+1}^{\infty} \left(\log\frac{1}{1-p}\right)^i/i! \\
\end{aligned}\end{equation}
注意$\log\frac{1}{1-p}\sim p$,所以后面的$\sum_{i=j+1}^{\infty}$部分,只对$p^{j+1}$及以上的项有贡献,因此我们就近乎显然地证明了右端展开式的前$j+1$项系数都是1!整个证明并不难理解,真正难的地方是勇敢将右端的求和推到无穷项,然后留意到误差部分只对$p^{j+1}$及以上有贡献,这是经典的逆向思维。
数学,妙不可言~
转载到请包括本文地址:https://kexue.fm/archives/10902
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Apr. 30, 2025). 《一道概率不等式:盯着它到显然成立为止! 》[Blog post]. Retrieved from https://kexue.fm/archives/10902
@online{kexuefm-10902,
title={一道概率不等式:盯着它到显然成立为止!},
author={苏剑林},
year={2025},
month={Apr},
url={\url{https://kexue.fm/archives/10902}},
}







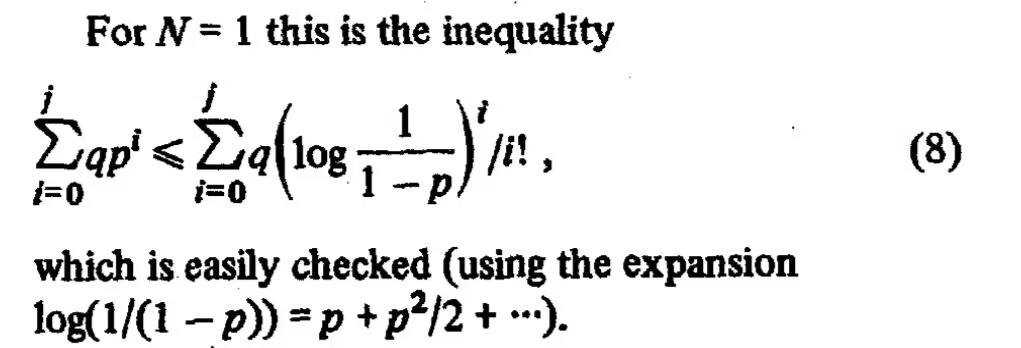



May 1st, 2025
论文中明确指出可以通过给定的泰勒展开式 easily check 该不等式,这让人自然而然地想到将泰勒展开代入原式,然后逐项对比。简单地代入后发现,对于 $\sum_{i=0}^{j} \frac{(\log \frac{1}{1 - p})^i}{i!}$ 的前 $j$ 项,其 $p^j$ 项的系数恒为 $1$,并且可以轻松验证到 $j = 4$ 的情形。我认为作者所说的 “check” 就是指这种方式。以下以$j = 4$举例:
\[\sum_{i=0}^{4} \frac{(\log \frac{1}{1 - p})^i}{i!}=
\log \frac{1}{1-p} + \frac{1}{2} \left(\log \frac{1}{1-p}\right)^2 + \frac{1}{6} \left(\log \frac{1}{1-p}\right)^3 + \frac{1}{24} \left(\log \frac{1}{1-p}\right)^4
\]
\[
={\left(p + \frac{p^2}{2} + \frac{p^3}{3} + \frac{p^4}{4} +\cdots\right)} + \frac{1}{2} \left(p + \frac{p^2}{2} + \frac{p^3}{3} +\cdots\right)^2 + \frac{1}{6} \left(p + \frac{p^2}{2} +\cdots\right)^3 + \frac{1}{24} \left(p + \cdots\right)^4
\]
\[
= p + \frac{p^2}{2} + \frac{p^3}{3} + \frac{p^4}{4} + \cdots + \frac{1}{2} \left[ p^2 + p^3 + \frac{1}{4} p^4 + 2 \times \frac{1}{3} p^4 + \cdots \right]
\]
\[
+ \frac{1}{6} \left[ p^3 + 3 \times \frac{1}{2} p^4 + \cdots \right] + \frac{1}{24} \left[ p^4 + \cdots \right]
\]
\[
= p + p^2 + p^3 + \left( \frac{1}{4} + \frac{1}{8} + \frac{1}{3} + \frac{1}{4} + \frac{1}{24} \right) p^4 + \cdots
\]
\[
= p + p^2 + p^3 + p^4 + \cdots \geq p + p^2 + p^3 + p^4
\]
接下来,我本以为可以很容易地推广到 $p$ 的任意次幂项,但实际操作时却发现,这样的推广并不容易。问题的关键在于,如果仍按照上述类似的方法,展开 $\frac{(\log \frac{1}{1 - p})^i}{i!}$ ,去求其对任意$p^j$ 项的贡献,似乎难以得到一个明确通用的表达式。
此路似乎不通。若转而采用泰勒展开求对应的 $n$ 阶导数,处理起来会简单很多。但我仍希望尝试最直接的做法,即直接计算该表达式中 $p^n$ 项的系数,并验证它为 $1$。
换一种思路来看,一个泰勒展开的多项式与自身多次相乘,最终的 $x^n$ 项来自于每个多项式因子$x^i$的组合贡献。例如,若最终目标是得到 $x^4$ 项,且指定是3个多项式相乘,那么必然有两个因子提供 $x^1$,另一个因子提供了 $x^2$,这样指数相加才为 $4$。这样的一组三个因子,它们的系数相乘,贡献了$x^4$的一部分系数。将所有这样满足要求的三元因子系数之积相加,则为这三个多项式相乘所提供的$x^4$的系数。我们虽然无法直接给出它具体等于多少,但是可以先用这样的叙述方式将其表达出来。
在本文给出的泰勒展开式$\log \frac{1}{1 - p} = \sum_{i=1}^{\infty} \frac{p^i}{i} = p + \frac{p^2}{2} + \frac{p^3}{3} + \cdots$中
,若某个因子的次数为 $i$,其前的系数即为 $\frac{1}{i}$。因此,可以将 $f_n(x) = \sum_{j=1}^{n} \frac{1}{j!} \left( \sum_{i=1}^{n} \frac{x_i}{i} \right)^j$中$x^n$ 项的系数表示为如下的 $T(n)$
\[
T(n) = \sum_{j=1}^{n} \frac{1}{j!} \sum_{\substack{i_1 + \cdots + i_j = n \\ i_1, \ldots, i_j \geq 1}} \frac{1}{i_1 \cdots i_j}
\]
接下来就可以用数学归纳法辅以一些变换技巧开始证明$T(n)=1$ 了。
易验证:
\[
T(1) = 1, \quad T(2) = 1, \quad T(3) = 1, \quad T(4) = 1
\]
假设对任意 $t < n$,都有 $T(t) = 1$, 现证 $T(n) = 1$:
\[
T(n) = \sum_{j=1}^{n} \frac{1}{j!} \sum_{\substack{i_1 + \cdots + i_j = n }} \frac{1}{i_1 \cdots i_j}
\]
\[
= \frac{1}{n} \left[ \sum_{j=1}^{n} \frac{1}{j!} \sum_{\substack{i_1 + \cdots + i_j = n}} \left( \frac{n}{i_1 \cdots i_j} \right) \right]
\]
单独分离出j=1的项。因为后续会将j减1,边界情况需单独处理
\[
= \frac{1}{n} \left[ \sum_{j=2}^{n} \frac{1}{j!} \sum_{\substack{i_1 + \cdots + i_j = n}} \left( \frac{i_1 + i_2 \cdots + i_j}{i_1 i_2 \cdots i_j} \right) + \sum_{i_1=n} \frac{n}{i_1}\right]
\]
\[
= \frac{1}{n} \left[ \sum_{j=2}^{n} \frac{1}{j!} \sum_{\substack{i_1 + \cdots + i_j = n}} \left( \frac{i_1 + i_2 + \cdots + i_j}{i_1 i_2 \cdots i_j} \right) + 1\right]
\]
\[
= \frac{1}{n} \left[ \sum_{j=2}^{n} \frac{1}{j!} \sum_{\substack{i_1 + \cdots + i_j = n }} \sum_{k=1}^{j} \frac{1}{i_1 \cdots i_{k-1} i_{k+1}\cdots i_j} +1 \right]
\]
交换求和符号
\[
= \frac{1}{n} \left[ \sum_{j=2}^{n} \frac{1}{j!} \sum_{k=1}^{j} \sum_{\substack{i_1 + \cdots + i_j = n }} \frac{1}{i_1 \cdots i_{k-1} i_{k+1}\cdots i_j} +1 \right]
\]
根据对称性,k分别取1,2,3...j中任意一值时,$\displaystyle\sum_{\substack{i_1 + \cdots + i_j = n }} \frac{1}{i_1 \cdots i_{k-1} i_{k+1}\cdots i_j}$都相等。
不妨取k=j,前面的求和符\(\sum_{k=1}^{j}\)可直接变为j
\[
= \frac{1}{n} \left[ \sum_{j=2}^{n} \frac{1}{j!} \cdot j\cdot \sum_{\substack{i_1 + \cdots + i_j = n }} \frac{1}{i_1 \cdots i_j} +1 \right]
\]
\[
= \frac{1}{n} \left[ \sum_{j=2}^{n} \frac{1}{(j-1)!} \sum_{\substack{i_1 + \cdots + i_j = n }} \frac{1}{i_1 \cdots i_j} + 1 \right]
\]
将 $i_j$ 固定为 $t$,则 $i_1 + \cdots + i_{j-1} = n - t$,
要保证每个$i$都至少为1,则$t$的取值范围为$[1,n-(j-1)]$
\[
= \frac{1}{n} \left[ \sum_{j=2}^{n} \frac{1}{(j-1)!} \sum_{t=1}^{n-(j-1)} \sum_{i_1+\cdots+i_{j-1}=n-t} \frac{1}{i_1 i_2 \cdots i_{j-1}} + 1 \right]
\]
用 \( t' = n - t \) 代替 \( t \),
则\( t' \)范围 \( [j-1, n-1] \)
\[
= \frac{1}{n} \left[ \sum_{j=2}^{n} \frac{1}{(j-1)!} \sum_{t'=j-1}^{n-1} \sum_{i_1+\cdots+i_{j-1}=t'} \frac{1}{i_1 i_2 \cdots i_{j-1}} + 1 \right]
\]
用 \( j' = j - 1 \) 代替 \( j \),
则\( j' \)范围 \( [1, n-1] \)
\[
= \frac{1}{n} \left[ \sum_{j'=1}^{n-1} \frac{1}{j'!} \sum_{t'=j'}^{n-1} \sum_{i_1+\cdots+i_{j'}=t'} \frac{1}{i_1 i_2 \cdots i_j'} + 1 \right]
\]
\[
= \frac{1}{n} \left[ \sum_{j'=1}^{n-1} \sum_{t'=j'}^{n-1} \frac{1}{j'!} \sum_{i_1+\cdots+i_{j'}=t'} \frac{1}{i_1 i_2 \cdots i_{j'}} + 1 \right]
\]
替换 \( t' \)为 \( t \), \( j' \) 为 \( j \)
\[
= \frac{1}{n} \left[ \sum_{j=1}^{n-1} \sum_{t=j}^{n-1} \frac{1}{j!} \sum_{i_1+\cdots+i_{j}=t} \frac{1}{i_1 i_2 \cdots i_{j}} + 1 \right]
\]
交换积分顺序
\[
= \frac{1}{n} \left[ \sum_{t=1}^{n-1}\sum_{j=1}^{t} \frac{1}{j!} \sum_{i_1+\cdots+i_{j}=t} \frac{1}{i_1 i_2 \cdots i_{j}} + 1 \right]
\]
\[
= \frac{1}{n} \left[ \sum_{t=1}^{n-1} T(t) + 1 \right]
\]
\[
= \frac{1}{n} \left[ (n-1) \cdot 1 + 1 \right] = 1
\]
得证。
佩服!直接用多项式乘法的直接定义,而没有用$n$次幂的多项式定理,反而使得证明过程更为可行。
我也尝试证明这个恒等式,发现太难了。最后盯出来的
May 5th, 2025
我也想进群可以吗?qq997707843
May 15th, 2025
A simple solution: Expand $-\log^{(1-p)}$ in terms of p and you will get the result in one line.
欢迎展示你的过程。
May 15th, 2025
Sorry I missed something :(