30
May
最小熵原理（三）：“飞象过河”之句模版和语言结构
By 苏剑林 | 2018-05-30 | 61986位读者 | 引用在前一文《最小熵原理（二）：“当机立断”之词库构建》中，我们以最小熵原理为出发点进行了一系列的数学推导，最终得到$(2.15)$和$(2.17)$式，它告诉我们两个互信息比较大的元素我们应该将它们合并起来，这有利于降低“学习难度”。于是利用这一原理，我们通过邻字互信息来实现了词库的无监督生成。
由字到词、由词到词组，考察的是相邻的元素能不能合并成一个好“套路”。可是套路为什么非得要相邻的呢？当然不一定相邻，我们学习语言的时候，不仅仅会学习到词语、词组，还要学习到“固定搭配”，也就是说词语怎么运用才是合理的，这是语法的体现，是本文所要探究的，希望最终能达到一定的无监督句法分析的效果。
由于这次我们考虑的是跨邻词的语言关联，因此我给它起个名字为“飞象过河”，正是
“套路宝典”第二式——“飞象过河”
语言结构
对于大多数人来说，并不会真正知道什么是语法，他们脑海里就只有一些“固定搭配”、“定式”，或者更正式一点可以叫“模版”。大多数情况下，我们是根据模版来说出合理的话来。而不同的人的说话模版可能有所不同，这就是个人的说话风格，甚至是“口头禅”。
7
Jul
从SamplePairing到mixup：神奇的正则项
By 苏剑林 | 2018-07-07 | 83459位读者 | 引用SamplePairing和mixup是两种一脉相承的图像数据扩增手段，它们看起来很不合理，而操作则非常简单，但结果却非常漂亮：在多个图像分类任务中都表明它们能提高最终分类模型的精度。
某些读者会困惑于一个问题：为什么如此不合理的数据扩增手段，能得到如此好的效果？而本文则要表明，它们看起来是一种数据扩增方法，事实上它们是对模型的一种正则化方案。正如周星驰的电影《国产凌凌漆》的一句经典台词：
表面上看这是一个吹风机，其实它是一个刮胡刀。
数据扩增
让我们从数据扩增说起。数据扩增是指我们在对原始数据做一些简单的变换后，它们对应的类别往往不会变化，所以我们可以在原来数据的基础上，“造”出更多的数据来。比如一幅小狗的照片，将它水平翻转、轻微的旋转、裁剪、平移等操作后，我们认为它的类别没有变化，它还是原来的那只狗。这样一来，从一个样本我们可以衍生出好几个样本，从而增加了训练样本量。
狗
旋转的狗
几年前，笔者曾经以自己对矩阵的粗浅理解写了一个“理解矩阵”系列，其中有一篇《为什么只有方阵有行列式？》讨论了非方阵的行列式问题，里边给出了“非方针的行列式不好看”和“方阵的行列式就够了”的观点。本文来再次思考这个问题。
首先回顾方阵的行列式，其实行列式最重要的价值在于它的几何意义：
n维方阵的行列式的绝对值，等于它的各个行（或列）向量所张成的n维立体的超体积。
这个几何意义是行列式的一切重要性的源头，相关的讨论可以参考《行列式的点滴》，它也是我们讨论非方阵行列式的基础。
分析
对于方阵$\boldsymbol{A}_{n\times n}$来说，可以将它看成$n$个行向量的组合，也可以看成$n$个列向量的组合，不管是哪一种，行列式的绝对值都等于这$n$个向量所张成的$n$维立体的超体积。换句话说，对于方阵来说，行、列向量的区分不改变行列式。
对于非方阵$\boldsymbol{B}_{n \times k}$就不一样了，不失一般性，假设$n > k$。我们可以将它看成$n$个$k$维行向量的组合，也可以看成$k$个$n$维列向量的组合。非方针的行列式，应该也具有同样含义，即它们所张成的立体的超体积。
我们来看第一种情况，如果看成$n$个$k$维行向量，那么就得视为这$n$个向量张成的$n$维体的超体积了，但是要注意$n > k$，因此这$n$个向量必然线性相关，因此它们根本就张不成一个$n$维体，也许是一个$n-1$维体甚至更低，这样一来，它的$n$维体的超体积自然为0。
但是第二种情况就没有那么平凡了。如果看成$k$个$n$维列向量，那么这$k$个向量虽然是$n$维的，但它们张成的是一个$k$维体，这$k$维体的超体积未必为0。我们就以这个非平凡的体积作为非方阵行列式的定义好了。
8
Jan
从动力学角度看优化算法（三）：一个更整体的视角
By 苏剑林 | 2019-01-08 | 62482位读者 | 引用
30
Jan
能量视角下的GAN模型（一）：GAN＝“挖坑”＋“跳坑”
By 苏剑林 | 2019-01-30 | 103248位读者 | 引用
“看那挖坑的人，有啥不一样～”
在这个系列中，我们尝试从能量的视角理解GAN。我们会发现这个视角如此美妙和直观，甚至让人拍案叫绝。
本视角直接受启发于Benjio团队的新作《Maximum Entropy Generators for Energy-Based Models》，这篇文章前几天出现在arxiv上。当然，能量模型与GAN的联系由来已久，并不是这篇文章的独创，只不过这篇文章做得仔细和完善一些。另外本文还补充了自己的一些理解和思考上去，力求更为易懂和完整。
作为第一篇文章，我们先来给出一个直白的类比推导：GAN实际上就是一场前仆后继（前挖后跳？）的“挖坑”与“跳坑”之旅～
总的来说，本文的大致内容如下：
1、给出了GAN/WGAN的清晰直观的能量图像；
2、讨论了判别器（能量函数）的训练情况和策略；
3、指出了梯度惩罚一个非常漂亮而直观的能量解释；
4、讨论了GAN中优化器的选择问题。
20
Jan
从Wasserstein距离、对偶理论到WGAN
By 苏剑林 | 2019-01-20 | 226538位读者 | 引用
推土机哪家强？成本最低找Wasserstein
2017年的时候笔者曾写过博文《互怼的艺术：从零直达WGAN-GP》，从一个相对通俗的角度来介绍了WGAN，在那篇文章中，WGAN更像是一个天马行空的结果，而实际上跟Wasserstein距离没有多大关系。
在本篇文章中，我们再从更数学化的视角来讨论一下WGAN。当然，本文并不是纯粹地讨论GAN，而主要侧重于Wasserstein距离及其对偶理论的理解。本文受启发于著名的国外博文《Wasserstein GAN and the Kantorovich-Rubinstein Duality》，内容跟它大体上相同，但是删除了一些冗余的部分，对不够充分或者含糊不清的地方作了补充。不管怎样，在此先对前辈及前辈的文章表示致敬。
（注：完整理解本文，应该需要多元微积分、概率论以及线性代数等基础知识。还有，本文确实长，数学公式确实多，但是，真的不复杂、不难懂，大家不要看到公式就吓怕了～）
21
Mar
细水长flow之可逆ResNet：极致的暴力美学
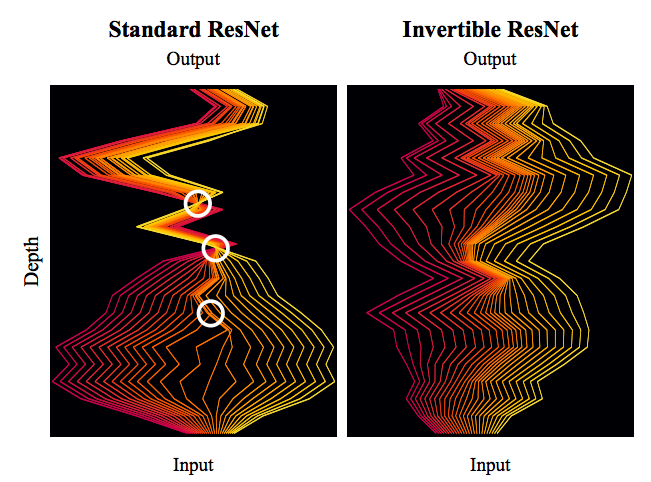
By 苏剑林 | 2019-03-21 | 120642位读者 | 引用今天我们来介绍一个非常“暴力”的模型：可逆ResNet。
为什么一个模型可以可以用“暴力”来形容呢？当然是因为它确实非常暴力：它综合了很多数学技巧，活生生地（在一定约束下）把常规的ResNet模型搞成了可逆的！
标准ResNet与可逆ResNet对比图。可逆ResNet允许信息无损可逆流动，而标准ResNet在某处则存在“坍缩”现象。
模型出自《Invertible Residual Networks》，之前在机器之心也报导过。在这篇文章中，我们来简单欣赏一下它的原理和内容。
可逆模型的点滴
为什么要研究可逆ResNet模型？它有什么好处？以前没有人研究过吗？
可逆的好处
可逆意味着什么？
意味着它是信息无损的，意味着它或许可以用来做更好的分类网络，意味着可以直接用最大似然来做生成模型，而且得益于ResNet强大的能力，意味着它可能有着比之前的Glow模型更好的表现～总而言之，如果一个模型是可逆的，可逆的成本不高而且拟合能力强，那么它就有很广的用途（分类、密度估计和生成任务，等等）。
19
Apr
从DCGAN到SELF-MOD：GAN的模型架构发展一览
By 苏剑林 | 2019-04-19 | 84420位读者 | 引用事实上，O-GAN的发现，已经达到了我对GAN的理想追求，使得我可以很惬意地跳出GAN的大坑了。所以现在我会试图探索更多更广的研究方向，比如NLP中还没做过的任务，又比如图神经网络，又或者其他有趣的东西。
不过，在此之前，我想把之前的GAN的学习结果都记录下来。
这篇文章中，我们来梳理一下GAN的架构发展情况，当然主要的是生成器的发展，判别器一直以来的变动都不大。还有，本文介绍的是GAN在图像方面的模型架构发展，跟NLP的SeqGAN没什么关系。
此外，关于GAN的基本科普，本文就不再赘述了。
棋盘效应图示，体现为放大之后出现如国际象棋棋盘一样的交错效应。图片来自文章《Deconvolution and Checkerboard Artifacts》
最近评论