从动力学角度看优化算法（三）：一个更整体的视角

最近把优化算法跟动力学结合起来思考得越来越起劲了，这是优化算法与动力学系列的第三篇，我有预感还会有第4篇，敬请期待～

简单来个剧情回顾：第一篇中我们指出了其实SGD相当于常微分方程（ODE）的数值解法：欧拉法；第二篇我们还是数值解法的误差分析的角度，分析了为什么可以通过梯度来调节学习率，因此也就解释了RMSprop、Adam等算法中，用梯度调节学习率的原理。

本文将给出一个更统一的观点来看待这两个事情，并且试图回答一个更本质的问题：为什么是梯度下降？

（注：本文的讨论没有涉及到动量加速部分。）

梯度下降再述 #

前两篇文章讨论的观点是“梯度下降相当于解ODE”，可是我们似乎还没有回答过，为什么是梯度下降？它是怎么来的？也就是说，之前我们只是在有了梯度下降之后，去解释梯度下降，还没有去面对梯度下降的起源问题。

下降最快的方向 #

基本的说法是这样的：梯度的反方向，是loss下降得最快的方向，所以要梯度下降。人们一般还会画出一个等高线图之类的示意图，来解释为什么梯度的反方向是loss下降得最快的方向。因此，很多人诟病RMSprop之类的自适应学习率优化器的原因也很简单：因为它们改变了参数下降的方向，使得优化不再是往梯度方向下降，所以效果不好。

但这样解释是不是足够合理了呢？

再描述一下问题 #

正式讨论之前，我们把问题简单定义一下：

1、我们有一个标量函数$L(\boldsymbol{\theta})\geq 0$，这里的参数$\boldsymbol{\theta}$可以是一个多元向量；

2、至少存在一个点$\boldsymbol{\theta}^*$，使得$L(\boldsymbol{\theta}^*)=0$，也就是说，$L(\boldsymbol{\theta})$的最小值就是0。

3、给定$L(\boldsymbol{\theta})$的具体形式，我们当然希望找到让$L(\boldsymbol{\theta})=0$的$\boldsymbol{\theta}$，就算不行，也希望找到一个$\boldsymbol{\theta}$让$L(\boldsymbol{\theta})$尽量小一些。

值得一提的是第2点，它其实并不是必要的，但有助于我们后面描述的一些探讨。也就是说，第2点其实只是一个假设，要知道，随便给我们一个函数，要我们求最小值的位置，但一般来说我们并不能事先知道它的最小值是多少；但是在深度学习中，这一点基本是成立的，因为我们通常会把loss设置成非负，并且得益于神经网络强大的拟合能力，loss很大程度上都能足够接近于0。

考虑loss的变化率 #

好，进入正题。假设在优化过程中参数$\boldsymbol{\theta}$按照某种轨迹$\boldsymbol{\theta}(t)$进行变化，那么$L(\boldsymbol{\theta})$也变成了$t$的函数$L(\boldsymbol{\theta}(t))$。注意这里的$t$不是真实的时间，它只是用来描述变化的参数，相当于迭代次数。

现在我们考虑$L(\boldsymbol{\theta}(t))$的变化率
\begin{equation}\frac{d}{dt}L(\boldsymbol{\theta}(t))=\left\langle\nabla_{\boldsymbol{\theta}}L,\, \dot{\boldsymbol{\theta}}\right\rangle\label{eq:ld}\end{equation}
这里$\dot{\boldsymbol{\theta}}$就是$d\boldsymbol{\theta}/dt$，$\langle\cdot\rangle$表示普通的内积。我们希望$L$越小越好，自然是希望上式右端为负数，而且绝对值越大越好。假如固定$\dot{\boldsymbol{\theta}}$的模长，那么要使得上式右端最小，根据内积的特点，$\nabla_{\boldsymbol{\theta}}L$和$\dot{\boldsymbol{\theta}}$的夹角应该要是180度，也就是
\begin{equation}\dot{\boldsymbol{\theta}} = -\lambda \nabla_{\boldsymbol{\theta}}L\quad (\lambda > 0)\label{eq:gd}\end{equation}
这也就说明了，梯度的反方向确实是loss下降最快的方向。而根据第一篇文章，上式不就是梯度下降？于是我们就很干脆地导出了梯度下降了。并且将$\eqref{eq:gd}$代入到$\eqref{eq:ld}$中，我们得到
\begin{equation}\frac{d}{dt}L(\boldsymbol{\theta}(t))=-\lambda\left\Vert\nabla_{\boldsymbol{\theta}}L\right\Vert^2\label{eq:ld-1}\end{equation}
这表明，只要学习率足够小（模拟ODE模拟到足够准确），并且$\nabla_{\boldsymbol{\theta}}L\neq \boldsymbol{0}$，那么$L$就一定会下降，直到$\nabla_{\boldsymbol{\theta}}L = 0$，这时候停留的位置，是个极小值点或者鞍点，理论上不可能是极大值点。此外，我们经常用的是随机梯度下降，mini-batch的做法会带来一定的噪声，而噪声在一定程度上能降低鞍点的概率（鞍点有可能对扰动不鲁棒），所以通常随机梯度下降效果比全量梯度下降要好些。

RMSprop再述 #

其实如果真的理解了上述推导过程，那么读者可以自己折腾出很多不同的优化算法出来。

不止有一个方向 #

比如，虽然前面已经证明了梯度的反方向是loss下降最快的方向，但凭什么就一定要往降得最快的的方向走呢？虽然梯度的反方向是堂堂正道，但也总有一些剑走偏锋的，理论上只要我保证能下降就行了，比如我可以取
\begin{equation}\dot{\boldsymbol{\theta}} = -\text{sign}\left(\nabla_{\boldsymbol{\theta}}L\right)\label{eq:rmsprop-1}\end{equation}
注意$\nabla_{\boldsymbol{\theta}}L$是一个向量，$\text{sign}\left(\nabla_{\boldsymbol{\theta}}L\right)$指的是对每一个分量取符号函数，得到一个元素是-1或0或1的向量。这样一来式$\eqref{eq:ld}$变为
\begin{equation}\frac{d}{dt}L(\boldsymbol{\theta}(t))=-\lambda\left\Vert\nabla_{\boldsymbol{\theta}}L\right\Vert_1\label{eq:ld-2}\end{equation}
其中$\Vert\boldsymbol{x}\Vert_1=\sum\limits_{i=1}^n |x_i|$表示向量的L1距离。这样选取也保证了loss在下降，理论上它收敛在$\nabla_{\boldsymbol{\theta}}L = 0$之处。

其实我们还有（假设梯度分量非零）
\begin{equation}\text{sign}\left(\nabla_{\boldsymbol{\theta}}L\right)=\frac{\nabla_{\boldsymbol{\theta}}L}{\sqrt{\nabla_{\boldsymbol{\theta}}L\otimes \nabla_{\boldsymbol{\theta}}L}}\label{eq:rmsprop-2}\end{equation}
结合$\eqref{eq:rmsprop-1}$和第二篇文章，再配合滑动平均，可以发现这一节说的就是RMSprop算法。

也就是说，自适应学习率优化器中，“学习率变成了向量，使得优化方向不再是梯度方向”根本不是什么毛病，也就不应该是自适应学习率优化器被人诟病之处。

不走捷径会怎样 #

但事实上是，真的精细调参的话，通常来说自适应学习率最终效果真的是不如SGD，说明自适应学习率优化器确实是有点毛病的。也就是说，如果你剑走偏锋，虽然一开始你走的比别人快，后期你就不如别人了。

毛病在哪呢？其实，如果是Adagrad，那问题显然是“太早停下来了”，因为它将历史梯度求和了（而不是平均），导致后期学习率太接近0了；如果是上面说的RMSprop，那么问题是——“根本停不下来”。

其实结合$\eqref{eq:rmsprop-1}$和$\eqref{eq:rmsprop-2}$我们得到
\begin{equation}\dot{\boldsymbol{\theta}} = -\frac{\nabla_{\boldsymbol{\theta}}L}{\sqrt{\nabla_{\boldsymbol{\theta}}L\otimes \nabla_{\boldsymbol{\theta}}L}}\label{eq:rmsprop-3}\end{equation}
这个算法什么时候停下来呢？实际上它不会停，因为只要梯度分量非零，那么对应的$\frac{\nabla_{\boldsymbol{\theta}}L}{\sqrt{\nabla_{\boldsymbol{\theta}}L\otimes \nabla_{\boldsymbol{\theta}}L}}$的分量也非零（不是1就是-1），从而在理论上看，这个算法并没有不动点，所以它根本不会停。为了缓解这个情况，所以RMSprop在实际使用的时候，采取了对分母滑动平均、加上epsilon（防止除零错误）这两个技巧。

但这只能算是缓解了问题，用ODE的话说就是“这个ODE并不是渐近稳定的”，所以终究会经常与局部最优点插肩而过。这才是自适应学习率算法的问题。

一点捣鼓 #

前面说了，如果真的理解过这个过程，其实自己都可以捣鼓出一些“独创的”优化算法出来，顺便还分析收敛情况。下面介绍我自己的一个捣鼓过程，还让我误以为是一个能绝对找出全局最优点的优化器～

（观看下面内容之前，请确保自己已经理解前述内容，否则可能造成误导～）

以全局最优为导向 #

这个捣鼓的出发点在于，不管是$\eqref{eq:gd}$（对应的收敛速率为$\eqref{eq:ld-1}$）还是$\eqref{eq:rmsprop-3}$（对应的收敛速率为$\eqref{eq:ld-2}$），就算它们能收敛，都只能保证$\nabla_{\boldsymbol{\theta}}L = 0$，无法保证是全局最优点（也就是不一定能做到$L(\boldsymbol{\theta})=0$）。于是一个很简单的想法是：既然我们已经知道了最小值是零，为什么不把这个信息加上去呢？

于是类比前面的思考过程，我们可以考虑：
\begin{equation}\dot{\boldsymbol{\theta}} = -\frac{\nabla_{\boldsymbol{\theta}}L}{\left\Vert\nabla_{\boldsymbol{\theta}}L\right\Vert^2}L\label{eq:me-gd}\end{equation}
这时候式$\eqref{eq:ld}$变得非常简单
\begin{equation}\frac{d}{dt}L=-L\end{equation}
这只是一个普通的线性微分方程呀，而且解是$L(t)=e^{-t}$，随着$t\to+\infty$，$L(t)\to 0$，也就是说loss一定能收敛到零。

真有这样的好事？ #

当然没有～我们来看式$\eqref{eq:me-gd}$，如果跑到了一个局部最优点，满足$\nabla_{\boldsymbol{\theta}}L=\boldsymbol{0},\,L > 0$，那么式$\eqref{eq:me-gd}$的右端就是负无穷了，这在理论上没有问题，但是在数值计算上是无法实现的。开始我以为这个问题很容易解决，似乎对分母加个epsilon避开原点就行了。但进一步分析才发现，这个问题是致命性的。

为了观察原因，我们把式$\eqref{eq:me-gd}$改写为
\begin{equation}\dot{\boldsymbol{\theta}} = -\frac{\nabla_{\boldsymbol{\theta}}L}{\left\Vert\nabla_{\boldsymbol{\theta}}L\right\Vert}L\times\frac{1}{\left\Vert\nabla_{\boldsymbol{\theta}}L\right\Vert}\label{eq:me-gd-2}\end{equation}
问题就在于$1/\left\Vert\nabla_{\boldsymbol{\theta}}L\right\Vert$会变得无穷大（出现了奇点），那能不能做个截断？比如考虑
\begin{equation}\dot{\boldsymbol{\theta}} = -\frac{\nabla_{\boldsymbol{\theta}}L}{\left\Vert\nabla_{\boldsymbol{\theta}}L\right\Vert}L\times\min\left(\frac{1}{\left\Vert\nabla_{\boldsymbol{\theta}}L\right\Vert},M\right)\label{eq:me-gd-3}\end{equation}
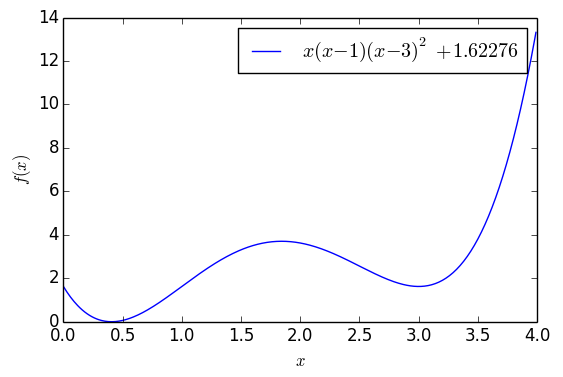
其中$M \gg 0$是个常数，这样就绕开了奇点。这样子做倒是真的能绕开一些局部最优点，比如下面的例子：

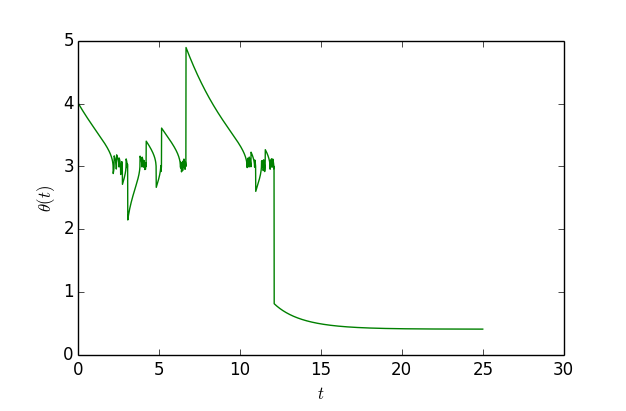
这个函数大约在$x=0.41$之间有一个全局最优点，函数值能取到0，但是在$x=3$的时候有一个次最优点。如果以$x_0=4$为初始值，单纯是用梯度下降的话，那么基本上都会收敛到$x=3$，但是用$\eqref{eq:me-gd-3}$，还是从$x_0=4$出发，那么经过一定振荡后，最终能收敛到$x=0.41$附近：

可以看到，开始确实会在$x=3$附近徘徊，振荡一段时间后就跳出来了，到了$x=0.41$附近。作图代码：

import numpy as np
import matplotlib.pyplot as plt


def f(x):
    return x * (x - 1) * (x - 3) * (x - 3) + 1.62276

def g(x):
    return -9 + 30 * x - 21 * x**2 + 4 * x**3

ts = [0]
xs = [4]
h = 0.01
H = 2500

for i in range(H):
    x = xs[-1]
    delta = -np.sign(g(x)) * min(abs(g(x)) / g(x)**2, 1000) * f(x)
    x += delta * h
    xs.append(x)
    ts.append(ts[-1] + h)

print f(xs[-1])
plt.figure()
plt.clf()
plt.plot(ts, xs, 'g')
plt.legend()
plt.xlabel('$t$')
plt.ylabel('$\\theta(t)$')
plt.show()

然而，看上去很美好，实际上它没有什么价值，因为真的要保证跳出所有的局部最优点，$M$必须足够大（这样才能跟原始的$\eqref{eq:me-gd-2}$足够接近），而且迭代步数足够多。但如果真能达到这个条件，其实还不如我们自己往梯度下降中加入高斯噪声，因为在第一篇文章我们已经表明，如果假设梯度的噪声是高斯的，那么从概率上来看，总能达到全局最优点（也需要迭代步数足够多）。所以，这个看上去很漂亮的玩意，并没有什么实用价值。

（注：后来阅读得知，原来Polyak很早就已经研究过式$\eqref{eq:me-gd}$形式的学习率，搜索“Polyak step size”就可以找到很多相关工作，比如《Revisiting the Polyak step size》、《Generalized Polyak Step Size for First Order Optimization with Momentum》等。）

文章小结 #

好了，哆里哆嗦捣鼓了一阵，又水了一篇文章。个人感觉从动力学角度来分析优化算法是一件非常有趣的事情，它能让你以一种相对轻松的角度来理解优化算法的魅力，甚至能将很多方面的知识联系起来。

一般的理解优化算法的思路，是从凸优化出发，然后把凸优化的结果不严格地用到非凸情形中。我们研究凸优化，是因为“凸性”对很多理论证明都是一个有力的条件，然而深度学习几乎处处都是非凸的。既然都已经是非凸了，也就是凸优化中的证明完备的这一优点已经不存在了，我觉得倒不如从一个更轻松的角度来看这个事情。这个更轻松的角度，就是动力系统，或者说常微分方程组。

事实上，这个视角的潜力很大，包括GAN的收敛分析，以及脍炙人口的“神经ODE”，都终将落到这个视角来。当然这些都是后话了～

转载到请包括本文地址：https://kexue.fm/archives/6261

更详细的转载事宜请参考：《科学空间FAQ》