为方轮自行车铺路

你见过正方形轮子的自行车吗？一般认为，只有圆形的车轮才能使我们的车子平稳向前移动，但这只是针对平直道路而言的。谁规定路一定是平的？只要铺好一条适当的道路，正方形车轮的自行车照样可以平稳前行！本文就让我们为方轮自行车铺一条路。

其实，方轮自行车已经不是新鲜玩意了，它早已出现在不少科技馆中。从图片中可以看到，它的特殊轨道是有许多段弧组成的，每一段弧的长度等于正方形的边长。车轮前行时，正方形会保持与弧形相切（确保不会打滑）。这样的路的形状是什么曲线呢？很幸运，它并不十分复杂，而且让人意外的是，它就是我们之前已经研究过的“悬链线”！原来，要设计这样的一个曲线的轨道，不需要多么高深的设计师，只需要我们手拿一条铁链，让它自由垂下......

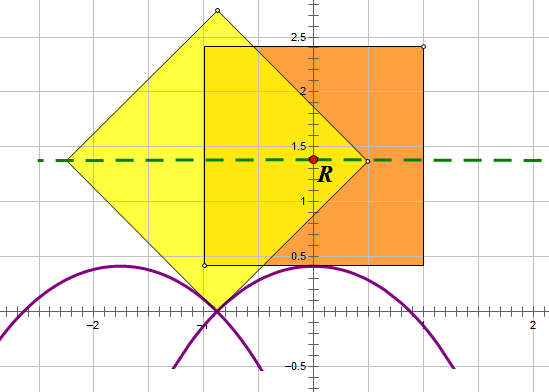
如图，这是方轮的两个特殊位置，设正方形的边长为2，由图不难得知，如果以x轴为地面的话，轮轴(R)与地面的距离为$\sqrt{2}$，中间的顶点与地面的距离为$\sqrt{2}-1$。

将各个点标记如下图

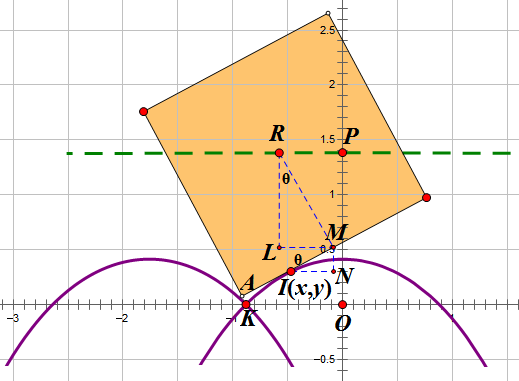
$y=y(x)$为轨道方程，其中$I(x,y)$是正方形车轮与“道路”的一个切点，根据道路与车轮的关系，线段AI的长度要等于弧KI的长，记该长为s，用微积分的符号表示为

$$s=\int_{x_0}^x \sqrt{dx^2+dy^2}=\int_{x_0}^x \sqrt{1+\dot{y}^2}dx$$
（$x_0$是左端的一个零点）

同时，我们有以下关系：

$$\begin{aligned}AI=s,MI=1-s,RM=1 \\ RM \cos\theta+MI \sin\theta+y=OP\end{aligned}$$

即$cos\theta+(1-s)sin\theta+y=\sqrt{2}$

从中解出s，并把$tan\theta=\dot{y}$代入，得到

$$s=1+\dot{y}^{-1}+y\sqrt{1+\dot{y}^{-2}}-\sqrt{2}\cdot \sqrt{1+\dot{y}^{-2}}$$

将两个s用等号联系起来，得到积分方程

$$\int_{x_0}^x \sqrt{1+\dot{y}^2}dx=1+\dot{y}^{-1}+y\sqrt{1+\dot{y}^{-2}}-\sqrt{2}\cdot \sqrt{1+\dot{y}^{-2}}$$

为了将其变成常见的微分方程，将两端取导数

等号左边取导数后变成
$$\sqrt{1+\dot{y}^2}$$

等号右边取导数后变成
$$-\dot{y}^{-2}\ddot{y}+(y-\sqrt{2})\cdot \frac{-\dot{y}^{-2}\ddot{y}}{\sqrt{1+\dot{y}^2}}+\sqrt{1+\dot{y}^2}$$

对消后变成：
$$\sqrt{2}-y=\sqrt{1+\dot{y}^2}$$

可以化为：$\frac{dx}{dy}=\frac{1}{\sqrt{(\sqrt{2}-y)^2-1}}$

即
$$\begin{aligned}-x=\int \frac{1}{\sqrt{(\sqrt{2}-y)^2-1}} d(\sqrt{2}-y) \\ =arccosh(\sqrt{2}-y)+C\end{aligned}$$

改写成
$$y=-\cos h(-C-x)+\sqrt{2}=-\cos h(C+x)+\sqrt{2}$$
（$cosh x$是双曲余弦函数，$cosh x=\frac{e^x+e^{-x}}{2}$）

根据初始条件，可以得出C=0，于是最终的轨道方程为
$$y=-\cos hx+\sqrt{2}$$
（取x轴上方的部分）

这是一条悬链线。神奇的悬链线！

解答完这个问题后，读者很自然地会有延伸出一个问题：对于任意正n边形的车轮，满足平稳前行的道路形状又该是怎样的呢？

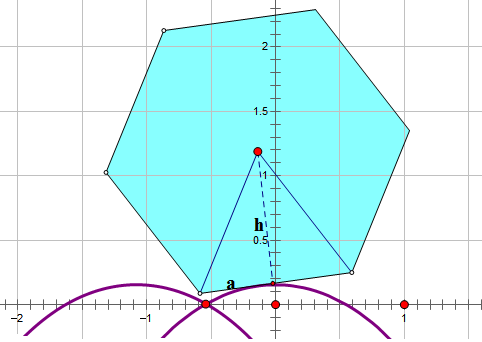
答案让人很惊喜，即并没有变得很繁，它依旧只是一条悬链线！如图，设正n边形的边长为2a，高为h，那么最终的答案将是：

$$y=-h \cos h(\frac{x}{h})+\sqrt{a^2+h^2}$$

如果以h=1为单位长度，根据$a=h*tan(\frac{\pi}{n})$，得到：

$$y=-\cos h x+\sqrt{1+\tan^2(\frac{\pi}{n})}$$

这只不过是正方形车轮的轨道向下平移了一点而已！

当n趋向无穷时，正n边形就变成了一个圆了，常识告诉我们，这时的路面应该是一条直线；可是此时路面方程变成了$y=-cosh x+1$，读者可能会疑惑为什么不是一条直线呢？有这样疑问的读者别忘了，我们已经说过轨道方程只取x轴上方的部分(y≥0)，然后水平拼接而成的。对于这条轨道方程只有(0,0)这一个点满足y≥0的，取这样的点无限拼接起来，就成了一条直线了！

至此，我们为方轮自行车的铺路之旅完毕！这个结果让我再次惊叹大自然的神秘。那在重力场自然垂下的一条铁链的形状，竟然为方轮自行车铺好了道路。冥冥中似乎总有一种神秘的力量，将各个看似毫不相关的东西联系了起来，这也许就是数学最令人激动人心的地方。

转载到请包括本文地址：https://kexue.fm/archives/1630

更详细的转载事宜请参考：《科学空间FAQ》