科学空间|Scientific Spaces

上一篇文章《生成扩散模型漫谈（二十二）：信噪比与大图生成（上）》中，我们介绍了通过对齐低分辨率的信噪比来改进noise schedule，从而改善直接在像素空间训练的高分辨率图像生成（大图生成）的扩散模型效果。而这篇文章的主角同样是信噪比和大图生成，但做到了更加让人惊叹的事情——直接将训练好低分辨率图像的扩散模型用于高分辨率图像生成，不用额外的训练，并且效果和推理成本都媲美直接训练的大图模型！

这个工作出自最近的论文《Upsample Guidance: Scale Up Diffusion Models without Training》，它巧妙地将低分辨率模型上采样作为引导信号，并结合了CNN对纹理细节的平移不变性，成功实现了免训练高分辨率图像生成。

思想探讨

我们知道，扩散模型的训练目标是去噪（Denoise，也是DDPM的第一个D）。按我们的直觉，去噪这个任务应该是分辨率无关的，换句话说，理想情况下低分辨率图像训练的去噪模型应该也能用于高分辨率图像去噪，从而低分辨率的扩散模型应该也能直接用于高分辨率图像生成。

点击阅读全文...

目前在LLM中最流行的Tokenizer（分词器）应该是Google的SentencePiece了，因为它符合Tokenizer的一些理想特性，比如语言无关、数据驱动等，并且由于它是C++写的，所以Tokenize（分词）的速度很快，非常适合追求效率的场景。然而，它也有一些明显的缺点，比如训练速度慢（BPE算法）、占用内存大等，同时也正因为它是C++写的，对于多数用户来说它就是黑箱，也不方便研究和二次开发。

事实上，Tokenizer的训练就相当于以往的“新词发现”，而笔者之前也写过中文分词和最小熵系列文章，对新词发现也有一定的积累，所以很早之前就有自己写一版Tokenizer的想法。这几天总算腾出了时间初步完成了这件事情，东施效颦SentencePiece，命名为“BytePiece”。

Github：https://github.com/bojone/bytepiece

点击阅读全文...

用理论物理来卷机器学习已经不是什么新鲜事了，比如上个月介绍的《生成扩散模型漫谈（十三）：从万有引力到扩散模型》就是经典一例。最近一篇新出的论文《Self-Supervised Learning based on Heat Equation》，顾名思义，用热传导方程来做（图像领域的）自监督学习，引起了笔者的兴趣。这种物理方程如何在机器学习中发挥作用？同样的思路能否迁移到NLP中？让我们一起来读读论文。

基本方程

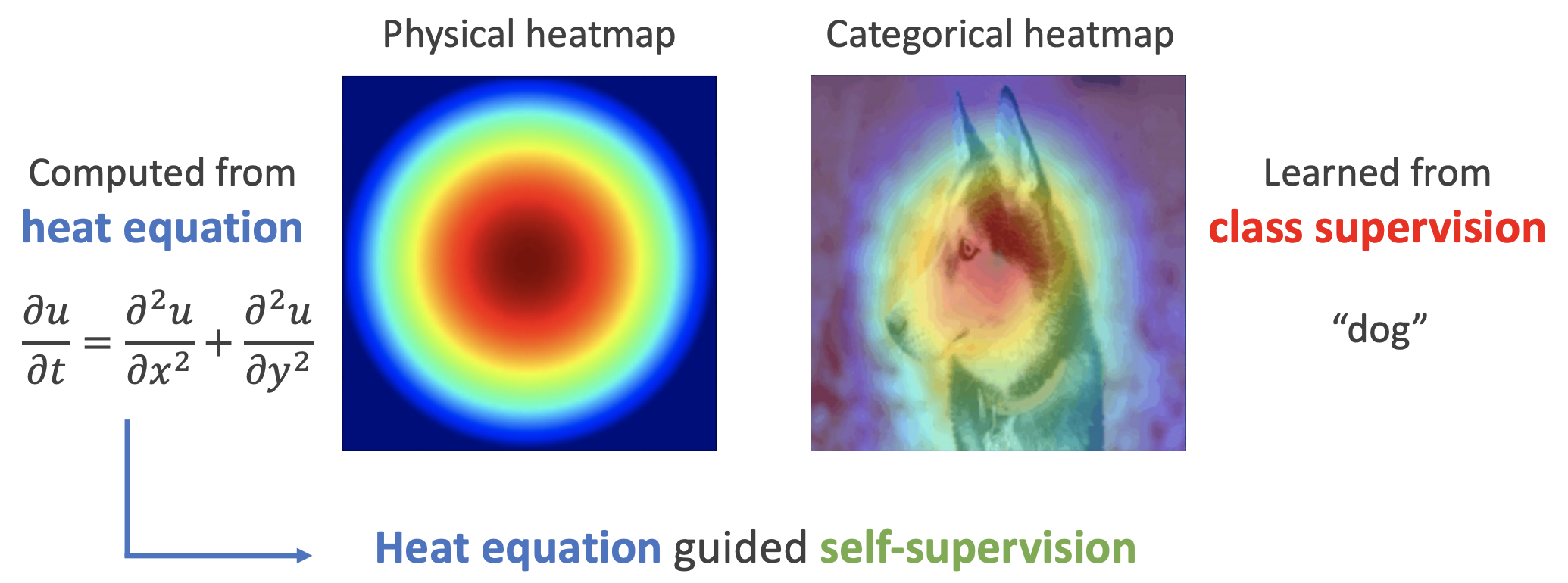
如下图，左边是物理中热传导方程的解，右端则是CAM、积分梯度等显著性方法得到的归因热力图，可以看到两者有一定的相似之处，于是作者认为热传导方程可以作为好的视觉特征的一个重要先验。

热方程的热力图（左）和视觉模型的热力图（右）

点击阅读全文...

当前，WGAN主流的实现方式包括参数裁剪（Weight Clipping）、谱归一化（Spectral Normalization）、梯度惩罚（Gradient Penalty），本来则来介绍一种新的实现方案：梯度归一化（Gradient Normalization），该方案出自两篇有意思的论文，分别是《Gradient Normalization for Generative Adversarial Networks》和《GraN-GAN: Piecewise Gradient Normalization for Generative Adversarial Networks》。

有意思在什么地方呢？从标题可以看到，这两篇论文应该是高度重合的，甚至应该是同一作者的。但事实上，这是两篇不同团队的、大致是同一时期的论文，一篇中了ICCV，一篇中了WACV，它们基于同样的假设推出了几乎一样的解决方案，内容重合度之高让我一直以为是同一篇论文。果然是巧合无处不在啊～

点击阅读全文...

在五花八门的预训练任务设计中，NSP通常认为是比较糟糕的一种，因为它难度较低，加入到预训练中并没有使下游任务微调时有明显受益，甚至RoBERTa的论文显示它会带来负面效果。所以，后续的预训练工作一般有两种选择：一是像RoBERTa一样干脆去掉NSP任务，二是像ALBERT一样想办法提高NSP的难度。也就是说，一直以来NSP都是比较“让人嫌弃”的。

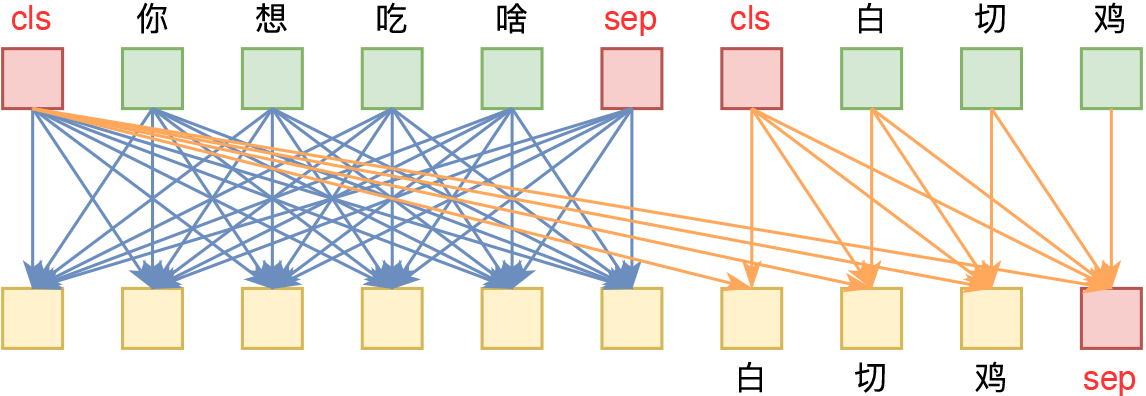
不过，反转来了，NSP可能要“翻身”了。最近的一篇论文《NSP-BERT: A Prompt-based Zero-Shot Learner Through an Original Pre-training Task--Next Sentence Prediction》（下面简称NSP-BERT）显示NSP居然也可以做到非常不错的Zero Shot效果！这又是一个基于模版（Prompt）的Few/Zero Shot的经典案例，只不过这一次的主角是NSP。

背景回顾

曾经我们认为预训练纯粹就是预训练，它只是为下游任务的训练提供更好的初始化，像BERT的预训练任务有MLM（Masked Language Model和NSP（Next Sentence Prediction），在相当长的一段时间内，大家都不关心这两个预训练任务本身，而只是专注于如何通过微调来使得下游任务获得更好的性能。哪怕是T5将模型参数训练到了110亿，走的依然是“预训练+微调”这一路线。

点击阅读全文...

大家都知道，Transformer的$\mathcal{O}(n^2)$复杂度是它的“硬伤”之一。不过凡事有弊亦有利，$\mathcal{O}(n^2)$的复杂度也为Transformer带来很大的折腾空间，我们可以灵活地定制不同的attention mask，来设计出不同用途的Transformer模型来，比如UniLM、K-BERT等。

本文介绍笔者构思的一个能用于文本的UniVAE模型，它沿用类似UniLM的思路，将VAE做到了一个Transformer模型里边，并且还具备多尺度特性～

UniAE式Attention关联示意图

点击阅读全文...

在《变分自编码器（五）：VAE + BN = 更好的VAE》中，我们讲到了NLP中训练VAE时常见的KL散度消失现象，并且提到了通过BN来使得KL散度项有一个正的下界，从而保证KL散度项不会消失。事实上，早在2018年的时候，就有类似思想的工作就被提出了，它们是通过在VAE中改用新的先验分布和后验分布，来使得KL散度项有一个正的下界。

该思路出现在2018年的两篇相近的论文中，分别是《Hyperspherical Variational Auto-Encoders》和《Spherical Latent Spaces for Stable Variational Autoencoders》，它们都是用定义在超球面的von Mises–Fisher（vMF）分布来构建先后验分布。某种程度上来说，该分布比我们常用的高斯分布还更简单和有趣～

KL散度消失

我们知道，VAE的训练目标是
\begin{equation}\mathcal{L} = \mathbb{E}_{x\sim \tilde{p}(x)} \Big[\mathbb{E}_{z\sim p(z|x)}\big[-\log q(x|z)\big]+KL\big(p(z|x)\big\Vert q(z)\big)\Big]
\end{equation}

点击阅读全文...

自SimCLR以来，CV中关于无监督特征学习的工作层出不穷，让人眼花缭乱。这些工作大多数都是基于对比学习的，即通过适当的方式构造正负样本进行分类学习的。然而，在众多类似的工作中总有一些特立独行的研究，比如Google的BYOL和最近的SimSiam，它们提出了单靠正样本就可以完成特征学习的方案，让人觉得耳目一新。但是没有负样本的支撑，模型怎么不会退化（坍缩）为一个没有意义的常数模型呢？这便是这两篇论文最值得让人思考和回味的问题了。

其中SimSiam给出了让很多人都点赞的答案，但笔者觉得SimSiam也只是把问题换了种说法，并没有真的解决这个问题。笔者认为，像SimSiam、GAN等模型的成功，很重要的原因是使用了基于梯度的优化器（而非其他更强或者更弱的优化器），所以不结合优化动力学的答案都是不完整的。在这里，笔者尝试结合动力学来分析SimSiam不会退化的原因。

SimSiam

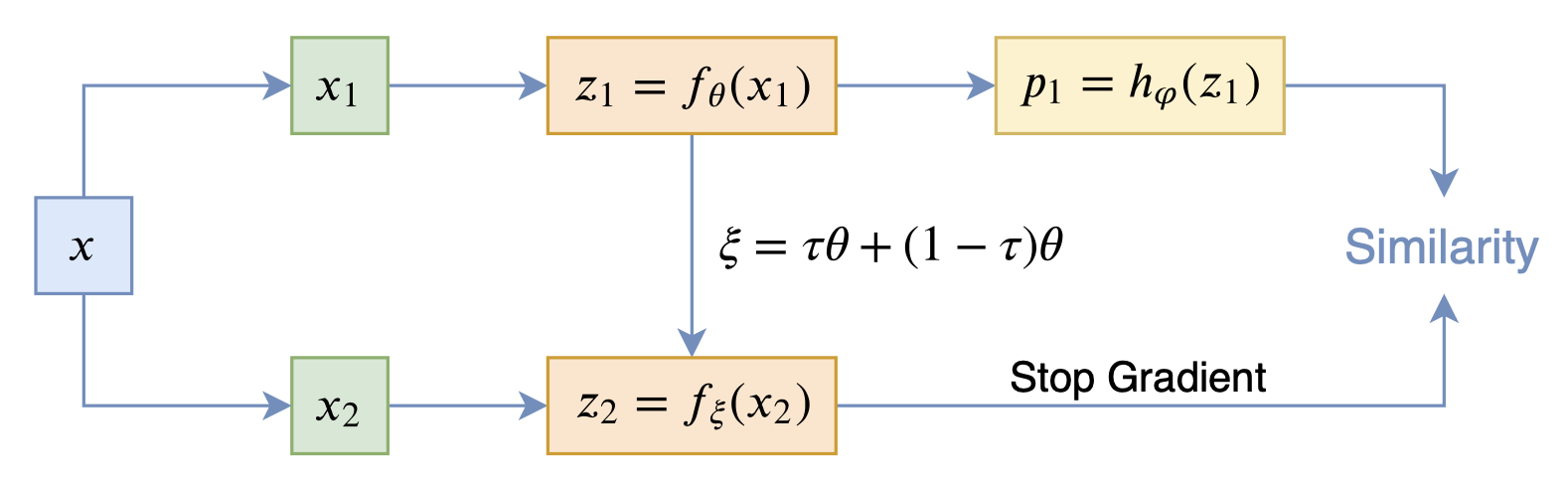
在看SimSiam之前，我们可以先看看BYOL，来自论文《Bootstrap your own latent: A new approach to self-supervised Learning》，其学习过程很简单，就是维护两个编码器Student和Teacher，其中Teacher是Student的滑动平均，Student则又反过来向Teacher学习，有种“左脚踩右脚”就可以飞起来的感觉。示意图如下：

BYOL示意图

点击阅读全文...