WGAN新方案:通过梯度归一化来实现L约束
By 苏剑林 | 2021-11-15 | 75359位读者 |当前,WGAN主流的实现方式包括参数裁剪(Weight Clipping)、谱归一化(Spectral Normalization)、梯度惩罚(Gradient Penalty),本来则来介绍一种新的实现方案:梯度归一化(Gradient Normalization),该方案出自两篇有意思的论文,分别是《Gradient Normalization for Generative Adversarial Networks》和《GraN-GAN: Piecewise Gradient Normalization for Generative Adversarial Networks》。
有意思在什么地方呢?从标题可以看到,这两篇论文应该是高度重合的,甚至应该是同一作者的。但事实上,这是两篇不同团队的、大致是同一时期的论文,一篇中了ICCV,一篇中了WACV,它们基于同样的假设推出了几乎一样的解决方案,内容重合度之高让我一直以为是同一篇论文。果然是巧合无处不在啊~
基础回顾 #
关于WGAN,我们已经介绍过多次,比如《互怼的艺术:从零直达WGAN-GP》和《从Wasserstein距离、对偶理论到WGAN》,这里就不详细重复了。简单来说,WGAN的迭代形式为:
\begin{equation}\min_G \max_{\Vert D\Vert_{L}\leq 1} \mathbb{E}_{x\sim p(x)}\left[D(x)\right] - \mathbb{E}_{z\sim q(z)}\left[D(G(z))\right]\end{equation}
这里的关键是判别器$D$是一个带约束优化问题,需要在优化过程中满足L约束$\Vert D\Vert_{L}\leq 1$,所以WGAN的实现难度就是如何往$D$里边引入该约束。
这里再普及一下,如果存在某个常数$C$,使得定义域中的任意$x,y$都满足$|f(x)-f(y)|\leq C\Vert x - y\Vert$,那么我们称$f(x)$满足Lipschitz约束(L约束),其中$C$的最小值,我们称为Lipschitz常数(L常数),记为$\Vert f\Vert_{L}$。所以,对于WGAN判别器来说,要做到两步:1、$D$要满足L约束;2、L常数要不超过1。
事实上,当前我们主流的神经网络模型,都是“线性组合+非线性激活函数”的形式,而主流的激活函数是“近线性的”,比如ReLU、LeakyReLU、SoftPlus等,它们的导函数的绝对值都不超过1,所以当前主流的模型其实都满足L约束,所以关键是如何让L常数不超过1,当然其实也不用非1不可,能保证它不超过某个固定常数就行。
方案简介 #
参数裁剪和谱归一化的思路是相似的,它们都是通过约束参数,保证模型每一层的L常数都有界,所以总的L常数也有界;而梯度惩罚则是留意到$\Vert D\Vert_{L}\leq 1$的一个充分条件是$\Vert \nabla_x D(x)\Vert \leq 1$,所以就通过惩罚项$(\Vert \nabla_x D(x)\Vert - 1)^2$来施加“软约束”。
本文介绍的梯度归一化,也是基于同样的充分条件,它利用梯度将$D(x)$变换为$\hat{D}(x)$,使其自动满足$\Vert\nabla_x \hat{D}(x)\Vert \leq 1$。具体来说,我们通常用ReLU或LeakyReLU作为激活函数,在这个激活函数之下,$D(x)$实际上是一个“分段线性函数”,这就意味着,除了边界之外,$D(x)$在局部的连续区域内都是一个线性函数,相应地,$\nabla_x D(x)$就是一个常向量。
于是梯度归一化就想着令$\hat{D}(x)=D(x)/\Vert \nabla_x D(x)\Vert$,这样一来就有
\begin{equation}\Vert\nabla_x \hat{D}(x)\Vert = \left\Vert \nabla_x \left(\frac{D(x)}{\Vert \nabla_x D(x)\Vert}\right)\right\Vert=\left\Vert \frac{\nabla_x D(x)}{\Vert \nabla_x D(x)\Vert}\right\Vert=1\end{equation}
当然,这样可能会有除0错误,所以两篇论文提出了不同的解决方案,第一篇(ICCV论文)直接将$|D(x)|$也加到了分母中,连带保证了函数的有界性:
\begin{equation} \hat{D}(x) = \frac{D(x)}{\Vert \nabla_x D(x)\Vert + |D(x)|}\in [-1,1]\end{equation}
第二篇(WACV论文)则是比较朴素地加了个$\epsilon$:
\begin{equation} \hat{D}(x) = \frac{D(x)\cdot \Vert \nabla_x D(x)\Vert}{\Vert \nabla_x D(x)\Vert^2 + \epsilon}\end{equation}
同时第二篇也提到试验过$\hat{D}(x)=D(x)/(\Vert \nabla_x D(x)\Vert+\epsilon)$,效果略差但差不多。
实验结果 #
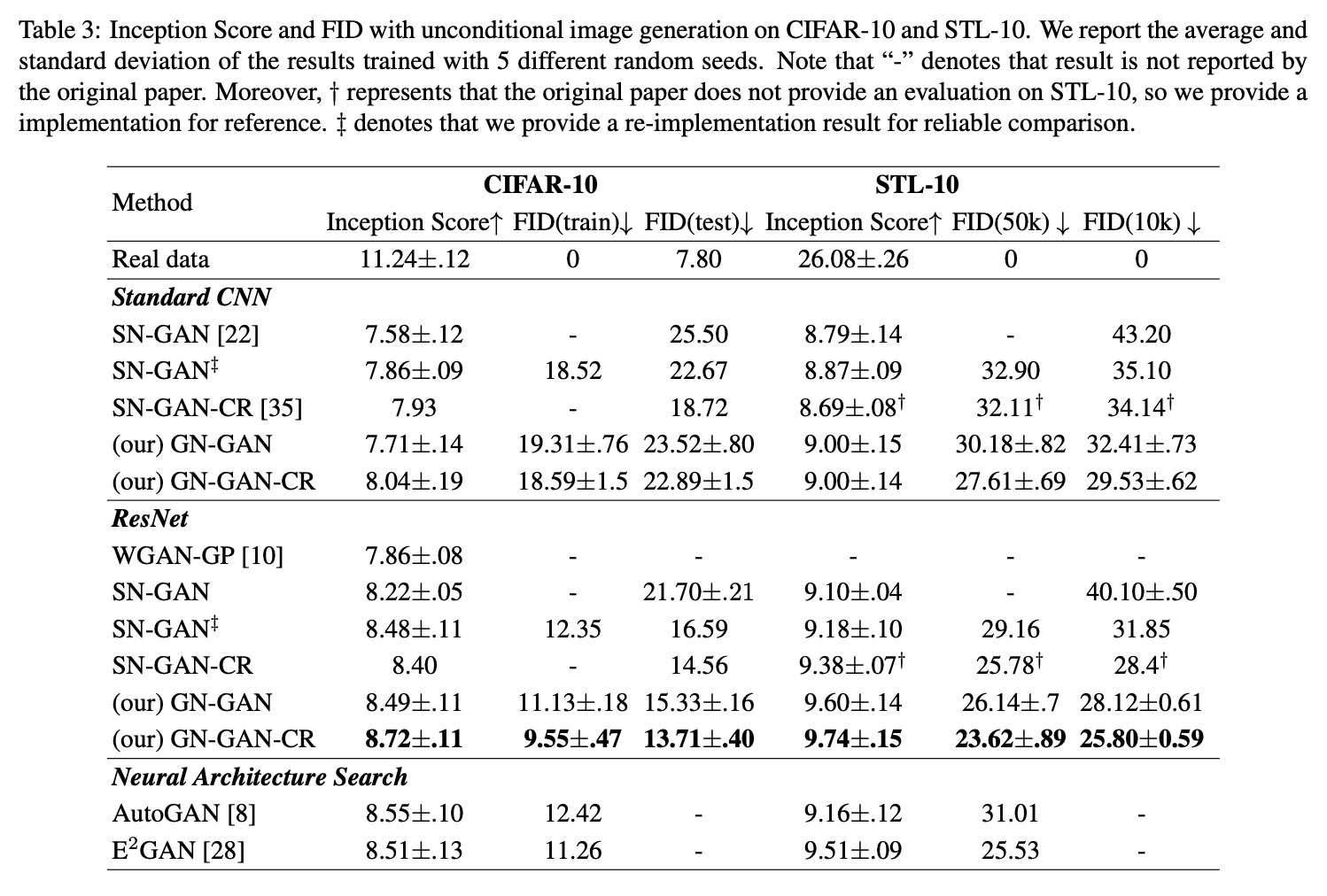
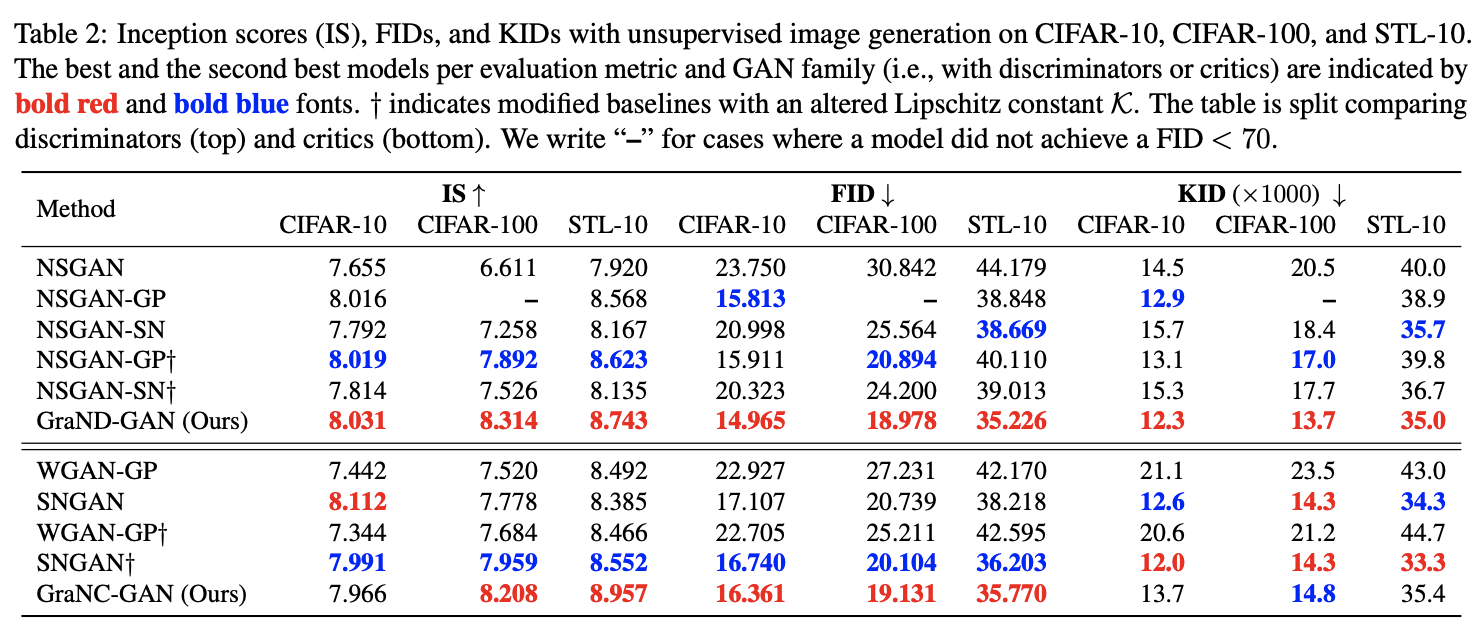
现在我们先来看看实验结果。当然,能双双中顶会,实验结果肯定是正面的,部分结果如下图:
尚有疑问 #
结果看上去很好,理论看上去也没问题,还同时被两个顶会认可,看上去是一个好工作无疑了。然而,笔者的困惑才刚刚开始。
该工作最重要的问题是,如果按照分段线性函数的假设,那么$D(x)$的梯度虽然在局部是一个常数,但整体来看它是不连续的(如果梯度全局连续又是常数,那么就是一个线性函数而不是分段线性了),然而$D(x)$本身是一个连续函数,那么$\hat{D}(x)=D(x)/\Vert \nabla_x D(x)\Vert$就是连续函数除以不连续函数,结果就是一个不连续的函数!
所以问题就来了,不连续的函数居然可以作为判别器,这看起来相当不可思议。要知道这个不连续并非只在某些边界点不连续,而是在两个区域之间的不连续,所以这个不连续是不可忽略的存在。在Reddit上,也有读者有着同样的疑问,但目前作者也没有给出合理的解释(链接)。
另一个问题是,如果分段线性函数的假设真的有效,那么我用$\hat{D}(x)=\left\langle \frac{\nabla_x D(x)}{\Vert \nabla_x D(x)\Vert}, x\right\rangle$作为判别器,理论上应该是等价的,但笔者的实验结果显示这样的$\hat{D}(x)$效果极差。所以,有一种可能性就是,梯度归一化确实是有效的,但其作用的原因并不像上面两篇论文分析的那么简单,也许有更复杂的生效机制我们还没发现。此外,也可能是我们对GAN的理解还远远不够充分,也就是说,对判别器的连续性等要求,也许远远不是我们所想的那样。
最后,在笔者的实验结果中,梯度归一化的效果并不如梯度惩罚,并且梯度惩罚仅仅是训练判别器的时候用到了二阶梯度,而梯度归一化则是训练生成器和判别器都要用到二阶梯度,所以梯度归一化的速度明显下降,显存占用量也明显增加。所以从个人实际体验来看,梯度归一化不算一个特别友好的方案。
文章小结 #
本文介绍了一种实现WGAN的新方案——梯度归一化,该方案形式上比较简单,论文报告的效果也还不错,但个人认为其中还有不少值得疑问之处。
转载到请包括本文地址:https://kexue.fm/archives/8757
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Nov. 15, 2021). 《WGAN新方案:通过梯度归一化来实现L约束 》[Blog post]. Retrieved from https://kexue.fm/archives/8757
@online{kexuefm-8757,
title={WGAN新方案:通过梯度归一化来实现L约束},
author={苏剑林},
year={2021},
month={Nov},
url={\url{https://kexue.fm/archives/8757}},
}











November 15th, 2021
感谢博主的分享!
关于博主探索的实验$\hat{D}(x)=\left\langle \frac{\nabla_x D(x)}{\Vert \nabla_x D(x)\Vert}, x\right\rangle$,这里跟D是分段线性的假设不是完全一致的,因为这里少了各个分段的偏移量。不知道博主有没有什么好的想法可以考虑进这个偏移量。
不好意思,我刚忘记归一化了,现在已经修正。
我指的是,我这样定义的$\hat{D}(x)$同样满足$\Vert\nabla_x \hat{D}(x)\Vert \leq 1$,并且理论上也具有万能拟合能力,所以应该可以作为具有同样功能的判别器,但事实上不能,所以基于线性假设的推导至少是不全面的。
此外,正如你所说,这个$\hat{D}(x)$跟梯度归一化所定义的$\hat{D}(x)$只是差一个偏移量,而在优化生成器的时候,由于使用的是基于梯度的优化器,这个偏移量的梯度为0,所以理论上基本不会影响结果。
感谢博主的回复。
在优化生成器时,的确单单看偏移量不会造成影响。但是在优化判别器的时候,是否建模该偏移量会影响判别器的学习,进而影响反馈给生成器的梯度。所以我认为偏移量是不应该被忽略的。
另外,想知道博主有没有像文中的两篇论文一样考虑分母为0或无穷的情况?
我也对网络的分段线性假设挺感兴趣,如果这个假设真的成立,除了在GAN上,通用的resnet等结构说不定都能得到新的启发。
我的意思,不是这样子能完全复制原论文的函数,而是说,如果假设$D(x)$是分段线性函数,那么我这里设计的$\hat{D}(x)$将会跟论文中的$\hat{D}(x)$具有一样的性质以及拟合能力,所以理论上应该得到至少相近的效果,但事实上得不到。
所以,依赖“$D(x)$是分段线性函数”去解释梯度归一化的效果,是不完全正确的。我有种感觉,就是我们只能假设$\Vert\nabla_x D(x)\Vert$是一个常数,而不能假设$\nabla_x D(x)$是一个常向量。
我自己用一个三层全连接层作为判别器做测试,中间激活函数用relu,用$\hat{D}(x)$回传到判别器全连接层偏置$b$的梯度会恒为0,而且通过推导发现,用$\hat{D}(x)$对全连接层的权值$w$求得的梯度跟用$D(x)$的区别确实与各层的$b$有关。这几天在学矩阵求导的一些方法时发现了一篇宝藏文,分享于此https://zhuanlan.zhihu.com/p/24709748
谢谢分享~
November 16th, 2021
苏神,想问下WACV跟ICCV是一个级别会议么?之前又看到wacv但是有没查到相关信息,含金量如何?
顶会这些我也不懂,网上查了一下评价,说是稍次于ICCV吧
December 10th, 2021
为什么希望判别器是连续的?
这是WGAN的L约束的要求。
December 13th, 2021
请教一下(2)式为何求导只对分子,而不对分母?
因为假设了分段线性函数,在一个连续区间内梯度为常向量,梯度模长为常数。
November 26th, 2023
请教一下哪里需要用到二阶导?(2)式不对分母求导的话应该不涉及到二阶导?
另外,实现的时候是不是应该将梯度的范数detach呢?
好像有点道理,又好像哪里不大对。如果这是对的,那么WGAN-GP的判别器是不是不能用relu激活?但好像没听说这个约束~