能量视角下的GAN模型(一):GAN=“挖坑”+“跳坑”
By 苏剑林 | 2019-01-30 | 148009位读者 |在这个系列中,我们尝试从能量的视角理解GAN。我们会发现这个视角如此美妙和直观,甚至让人拍案叫绝。
本视角直接受启发于Benjio团队的新作《Maximum Entropy Generators for Energy-Based Models》,这篇文章前几天出现在arxiv上。当然,能量模型与GAN的联系由来已久,并不是这篇文章的独创,只不过这篇文章做得仔细和完善一些。另外本文还补充了自己的一些理解和思考上去,力求更为易懂和完整。
作为第一篇文章,我们先来给出一个直白的类比推导:GAN实际上就是一场前仆后继(前挖后跳?)的“挖坑”与“跳坑”之旅~
总的来说,本文的大致内容如下:
1、给出了GAN/WGAN的清晰直观的能量图像;
2、讨论了判别器(能量函数)的训练情况和策略;
3、指出了梯度惩罚一个非常漂亮而直观的能量解释;
4、讨论了GAN中优化器的选择问题。
前“挖”后“跳” #
在这部分中,我们以尽量通俗的比喻来解释什么是能量视角下的GAN。
首先我们有一批样本$x_1,x_2,\dots,x_{n}$,我们希望能找到一个生成模型,这个模型有能力造出一批新的样本$\hat{x}_1,\hat{x}_2,\dots,\hat{x}_{n}$,我们希望这批新样本跟原样本很相似。怎么造呢?很简单,分两步走。
“挖坑” #
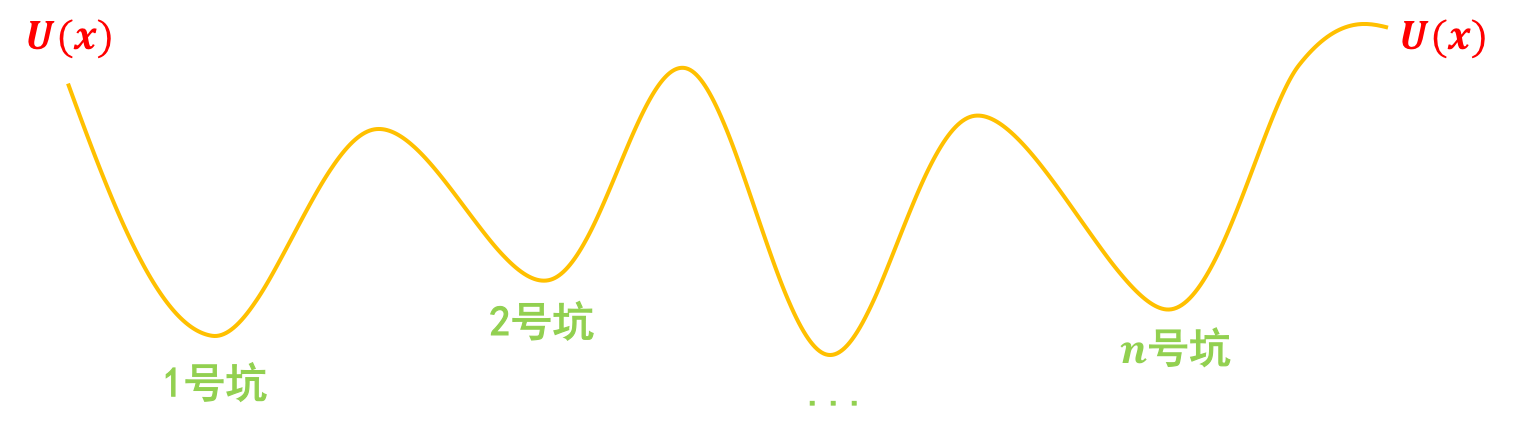
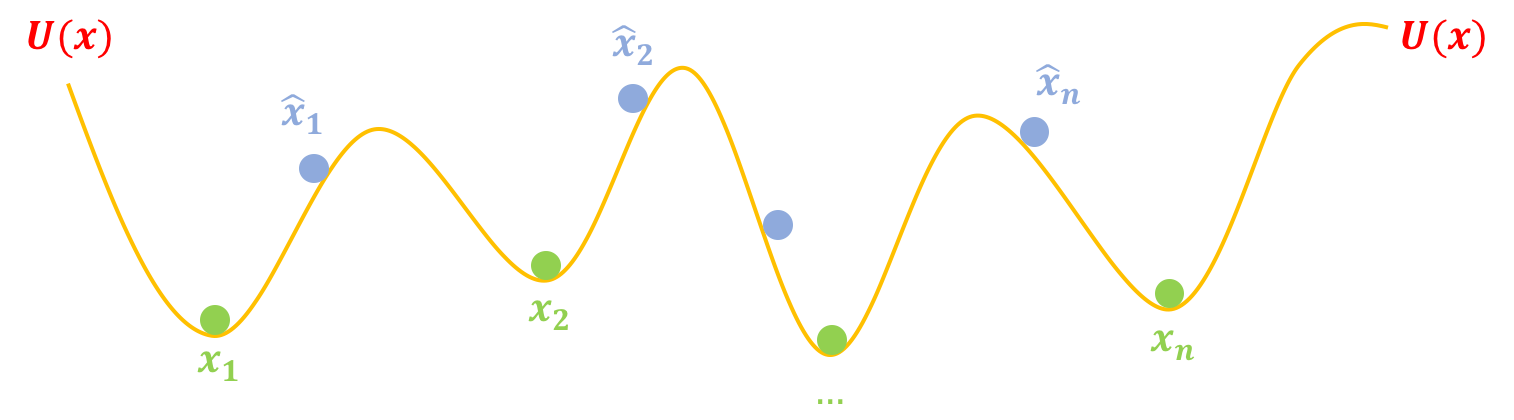
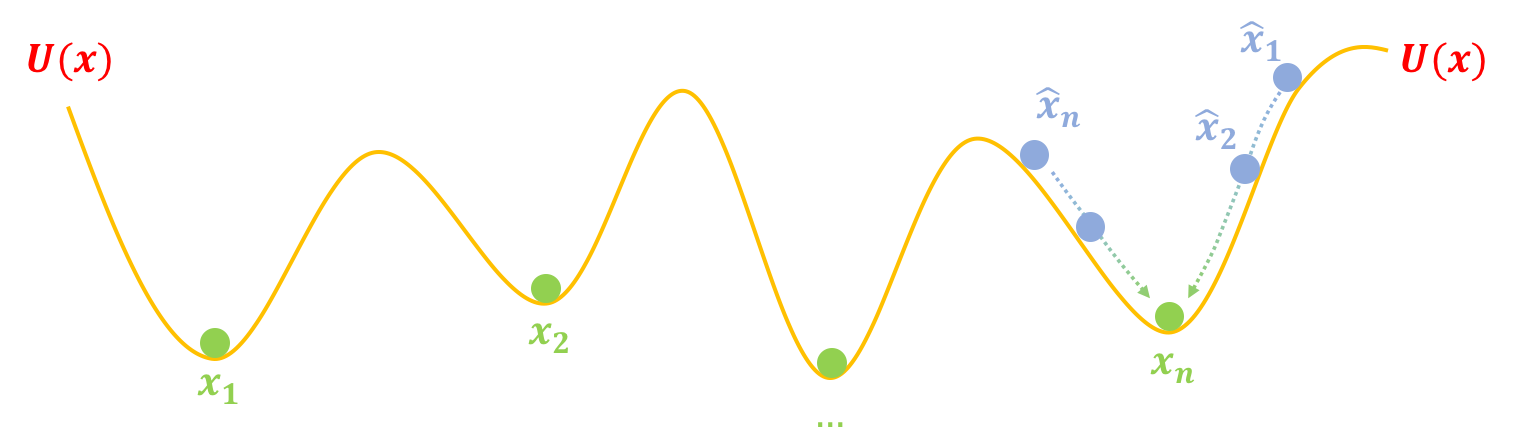
第一步,挖坑:我们把真实样本$x_1,x_2,\dots,x_{n}$看成一个个坐标,在这些坐标处挖很多坑,这些坑的分布可以用一个能量函数$U(x)$描述,这样一来真实样本$x_1,x_2,\dots,x_{n}$相当于都被放在坑底了,然后我们再把造出来的假样本$\hat{x}_1,\hat{x}_2,\dots,\hat{x}_{n}$放到“坑腰”:
“跳坑” #
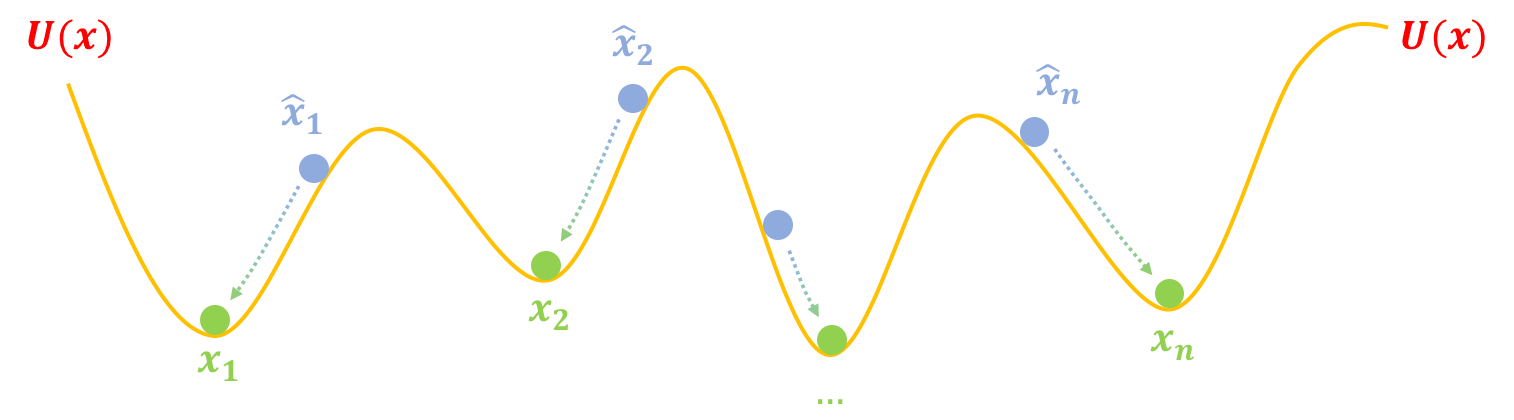
第二步,跳坑:把$U(x)$固定住,也就是不要再动坑了,然后把假样本$\hat{x}_1,\hat{x}_2,\dots,\hat{x}_{n}$松开,显然它们就慢慢从滚到坑底了,而坑底代表着真实样本,所以$\hat{x}_1,\hat{x}_2,\dots,\hat{x}_{n}$都变得很像真样本了:
这便是GAN的工作流程~
把GAN写下来 #
注意,上述两步不仅仅是简单的比喻,而是GAN的完整描述了。根据上述两个步骤,我们甚至可以直接把GAN训练公式写出来。
判别器 #
首先看“挖坑”,我们说了要将真样本放到坑底,假样本放到坑腰,以便后面假样本可以滚到坑底,这意味着假样本的“平均海拔”要高于真样本的“平均海拔”,也就是说
\begin{equation}\mathbb{E}_{x\sim p(x)}\big[U(x)\big] - \mathbb{E}_{x\sim q(x)}\big[U(x)\big]\label{eq:eq-e}\end{equation}
尽量小,这里我们用$p(x)$表示真实样本的分布,$q(x)$表示假样本的分布。假样本通过$x=G(z)$生成,而$z\sim q(z)$是标准正态分布。
梯度惩罚 #
另外,我们还说真样本要在坑底,用数学的话说,坑底就是一个极小值点,导数等于0才好,即要满足$\nabla_x U(x)=0$是最理想的,换成优化目标的话,那就是$\Vert \nabla_x U(x)\Vert^2$越小越好。两者综合起来,我们就得到$U$的优化目标
\begin{equation}\begin{aligned}U =& \mathop{\text{argmin}}_{U}\mathbb{E}_{x\sim p(x)}\big[U(x)\big] - \mathbb{E}_{x\sim q(x)}\big[U(x)\big] + \lambda \mathbb{E}_{x\sim p(x)}\big[\Vert \nabla_x U(x)\Vert^2\big]\\
=& \mathop{\text{argmin}}_{U}\mathbb{E}_{x\sim p(x)}\big[U(x)\big] - \mathbb{E}_{z\sim q(z)}\big[U(G(z))\big] + \lambda \mathbb{E}_{x\sim p(x)}\big[\Vert \nabla_x U(x)\Vert^2\big]
\end{aligned}\label{eq:eq-ee}\end{equation}
注:以往对于梯度惩罚,我们总会有两个困惑:1、梯度惩罚究竟是以0为中心好还是以1为中心好;2、梯度惩罚要对真样本、假样本还是真假插值样本进行?现在,基于能量视角,我们可以得到“对真样本进行以0为中心的梯度惩罚”比较好,因为这意味着(整体上)要把真样本放在极小值点处~
至此,在能量视角下,我们对梯度惩罚有了一个非常直观的回答。
生成器 #
然后看“跳坑”,也就是坑挖好了,$U$固定了,我们让假样本滚到坑底,也就是让$U(x)$下降,滚到最近的一个坑,所以
\begin{equation}G = \mathop{\text{argmin}}_{G}\mathbb{E}_{z\sim q(z)}\big[U(G(z))\big]\label{eq:eq-g}\end{equation}
可以看到,判别器实际上就是在“造势”,而生成器就是让势能最低,这便是能量GAN的主要思想~
交替训练 #
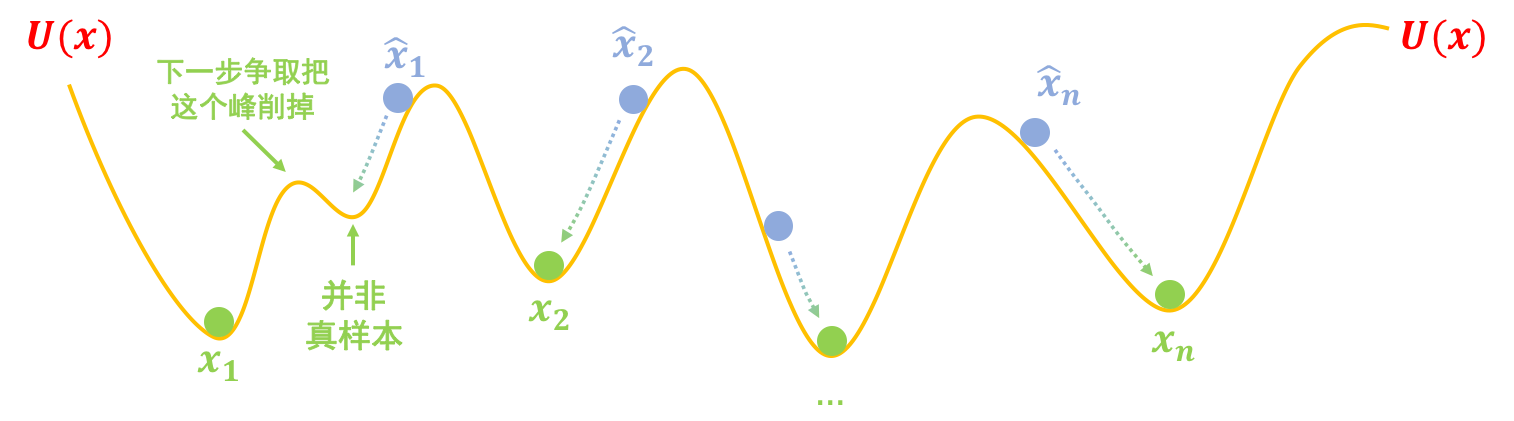
如果真实情况的坑都像上面的图那么简单,那么可能就只需要两步就能训练完一个生成模型了。但是真实情况下的坑可能是很复杂的,比如下图中假样本$\hat{x}_1$慢慢下滑,并不一定能到达$x_1$的坑,而是到达一个中间的坑,这个中间的坑并非代表真样本,可能仅仅是“次真”的样本,所以我们需要不断地改进假样本,也需要不断地把坑修正过来(比如争取能下一步把阻碍前进的峰“削掉”)。这也就是说,我们需要反复、交替地执行$\eqref{eq:eq-e},\eqref{eq:eq-g}$两步。
坑的学问 #
看,头脑中想象着几个坑,我们就可以把GAN的完整框架导出来了,而且还是先进的WGAN-GP的升级版:以0为中心的梯度惩罚。
GAN不过是一场坑的学问!
对这个GAN的进一步讨论,可以参考我之前写的博客《WGAN-div:一个默默无闻的WGAN填坑者》或者论文《Which Training Methods for GANs do actually Converge?》。
进一步思考 #
上述图景还能帮助我们回答很多问题。比如判别器能不能不要梯度惩罚?为什么GAN的训练、尤其是生成器的训练多数都不用带动量的优化器,或者就算用带动量的优化器,也要把动量调小一点?还有mode collapse(模式坍缩)是怎么发生呢?
Hinge Loss #
梯度惩罚在理论上很漂亮,但是它确实太慢,所以从实践角度来看,其实能不用梯度惩罚的话最好不用梯度惩罚。但是如果不用梯度惩罚,直接最小化式$\eqref{eq:eq-e}$,很容易数值不稳定。
这不难理解,因为没有约束情况下,很容易对于真样本有$U(x)\to -\infty$,对于假样本有$U(x)\to +\infty$,也就是判别器优化得太猛了,差距拉得太大(无穷大)了。那么一个很自然的想法是,分别给真假样本分别设置一个阈值,$U(x)$的优化超过这个阈值就不要再优化了,比如:
\begin{equation}\mathbb{E}_{x\sim p(x)}\big[\max(0, 1+U(x))\big] + \mathbb{E}_{x\sim q(x)}\big[\max(0,1-U(x))\big]\label{eq:eq-e-hinge}\end{equation}
这样一来,对于$x\sim p(x)$,如果$U(x) < -1$,则$\max(0, 1+U(x))=0$,对于$x\sim q(x)$,$U(x) > 1$,则$\max(0, 1-U(x))=0$,这两种情况下都不会在优化$U(x)$了,也就是说对于真样本$U(x)$不用太小,对于假样本$U(x)$不用太大,从而防止了$U(x)$过度优化了。
这个方案就是SNGAN、SAGAN、BigGAN都使用的hinge loss了。
当然,如果$U(x)$本身就是非负的[比如EBGAN中用自编码器的MSE作为$U(x)$],那么可以稍微修改一下式$\eqref{eq:eq-e-hinge}$:
\begin{equation}\mathbb{E}_{x\sim p(x)}\big[U(x)\big] + \mathbb{E}_{x\sim q(x)}\big[\max(0,m-U(x))\big]\label{eq:eq-e-hinge2}\end{equation}
其中$m > 0$。
优化器 #
至于优化器的选择,其实从“跳坑”那张图我们就可以看出答案来。
带动量的优化器有利于我们更快地找到更好的极小值点,但是对于GAN来说,其实我们不需要跑到更好的极小值点,我们只需要跑到最近的极小值点,如果一旦跳出了最近的极小值点,跑到更低的极小值点,那么可能就丧失了多样性,甚至出现mode collapse。
比如下图中的$\hat{x}_2$,不带动量的优化算法能让$\hat{x}_2$跑到$x_2$处就停下来,如果带动量的话,那么可能越过$x_2$甚至跑到$x_1$去了。尽管$x_1$也是真样本,但是这样一来$\hat{x}_1,\hat{x}_2$同时向$x_1$靠拢,也许没有假样本能生成$x_2$了,从而丧失了多样性。
所以,在GAN的优化器中,动量不能太大,太大反而有可能丧失生成样本的多样性,或者造成其他的不稳定情况。同理,学习率也不能太大。总之,一切加速手段都不能太猛了。
Mode Collapse #
什么是mode collapse?为什么会发生mode collapse?还是可以用这个图景来轻松解释。
前面我们画的图把假样本$\hat{x}$画得很合理,但是如果一旦初始化不好、优化不够合理等原因,使得$\hat{x}$同时聚在个别坑附近,比如:
这时候按照上述过程优化,所有假样本都都往$x_n$奔了,所以模型只能生成单一(个别)样式的样本,这就是mode collapse。
简单来看,mode collapse是因为假样本们太集中,不够“均匀”,所以我们可以往生成器那里加一个项,让假样本有均匀的趋势。这个项就是假样本的熵$H(X)=H(G(Z))$,我们希望假样本的熵越大越好,这意味着越混乱、越均匀,所以生成器的目标可以改为
\begin{equation}G = \mathop{\text{argmin}}_{G} -H(G(Z)) + \mathbb{E}_{z\sim q(z)}\big[U(G(z))\big]\label{eq:eq-gg}\end{equation}
这样理论上就能解决mode collapse的问题。至于$H(X)$怎么算,我们后面会详细谈到。
能量视角之美 #
对于GAN来说,最通俗易懂的视角当属“造假者-鉴别者”相互竞争的类比,这个视角直接导致了标准的GAN。但是,这个通俗的类比无法进一步延伸到WGAN乃至梯度惩罚等正则项的理解。
相比之下,能量视角相当灵活,它甚至能让我们直观地理解WGAN、梯度惩罚等内容,这些内容可以说是目前GAN领域最先进的部分成果了。虽然看起来能量视角比“造假者-鉴别者”形式上复杂一些,但其实它的物理意义也相当清晰,稍加思考,我们会感觉到它其实更为有趣、更具有启发性,有种“越嚼越有味”的感觉~
转载到请包括本文地址:https://kexue.fm/archives/6316
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Jan. 30, 2019). 《能量视角下的GAN模型(一):GAN=“挖坑”+“跳坑” 》[Blog post]. Retrieved from https://kexue.fm/archives/6316
@online{kexuefm-6316,
title={能量视角下的GAN模型(一):GAN=“挖坑”+“跳坑”},
author={苏剑林},
year={2019},
month={Jan},
url={\url{https://kexue.fm/archives/6316}},
}












January 20th, 2023
偶尔搜到您的网页,就被吸引了,这种最小势能的描述颇有上世纪70年代流行的风格,也是十几年前我上学时的主流描述,很亲切。看来时尚都是轮回的
可惜博客的风格还没有流行到“时尚”哈哈
June 30th, 2023
苏神,我之前看了一篇博客https://zhuanlan.zhihu.com/p/25071913,用公式从信息(分布)的角度推出了关于GAN中训练不稳定,以及出现mode collapse 原因。您这里说的加了一个-H(G(z)),是不是也可以理解为,就是在改进原始KL散度度量是不对称的问题,-H(G(z))的存在相当于增大了“生成器生成了不真实的样本”的惩罚。但是这种改进还是有问题的,还是不对称的。所以这么一看WGAN确实牛逼,但是优化器的选择是否也还会造成WGAN的mode collapse?我感觉好像会?还是说梯度约束也约束了它不会越坑乱跳?
WGAN其实也可能会mode collapse。从 https://kexue.fm/archives/9662 的视角看可能会更加精准一些:想要不collapse的生成器损失应该是那篇文章的式$(8)$,但实际上用的是那篇文章的式$(11)$,两者只有在单步优化的时候才等价,所以GAN的生成器都不能训练太多步,如果要训练多步,最好以篇文章的式$(8)$为loss
September 10th, 2023
想问下(1)式为什么不是E[U(x)]在q(x)分布下减去p(x)分布下?真样本才是参考点。
这个目标是最小化的哦,不是最大化。
May 28th, 2024
`然后看“跳坑”,也就是坑挖好了,U固定了,我们让假样本滚到坑底,也就是让U(x)下降,滚到最近的一个坑,所以...`
这个地方可能有些不清楚,优化的是G,其实是怎么生成假球(因为z理论上是一个随机变量)。似乎不是梯度下降假球。梯度下降的是对于任何z的假球置放策略。
有点看不懂你的问题...
不好意思,说的不太清楚
我的意思是其实G(z)并不是样本,应该是z的分布的映射,毕竟每次迭代的过程中,z都是在变得吧。这样其实小球向下滚这个表达就有些不太好理解了。
谢谢
$G$是生成器,它的输出$G(z)$就是样本呀。
January 21st, 2025
你公式1写反了?Ex∼p(x)[U(x)]−Ex∼q(x)[U(x)],px在坑底,相应的E也就最小,那公式1是小的减去大的,为负数,理想情况应为0,那应该是最大化公式1才对啊,你为啥写的要尽量最小,公式1尽量最小岂不是要Ex∼q(x)[U(x)]越大越好,E越大,海拔就越高,那不就远离坑底了吗?
这说的是“挖坑”的损失函数,也就是判别器的损失,你说的是生成器的损失。
March 23rd, 2025
为什么能假定假样本$x_i^{head}$能从一组正态分布中转换得到呢?
这是你的建模目标
May 28th, 2025
苏神用什么画图的呀,感觉很简洁大方
这篇文章的图,是ppt画的~