变分自编码器（五）：VAE + BN = 更好的VAE

本文我们继续之前的变分自编码器系列，分析一下如何防止NLP中的VAE模型出现“KL散度消失（KL Vanishing）”现象。本文受到参考文献是ACL 2020的论文《A Batch Normalized Inference Network Keeps the KL Vanishing Away》的启发，并自行做了进一步的完善。

值得一提的是，本文最后得到的方案还是颇为简洁的——只需往编码输出加入BN（Batch Normalization），然后加个简单的scale——但确实很有效，因此值得正在研究相关问题的读者一试。同时，相关结论也适用于一般的VAE模型（包括CV的），如果按照笔者的看法，它甚至可以作为VAE模型的“标配”。

最后，要提醒读者这算是一篇VAE的进阶论文，所以请读者对VAE有一定了解后再来阅读本文。

VAE简单回顾 #

这里我们简单回顾一下VAE模型，并且讨论一下VAE在NLP中所遇到的困难。关于VAE的更详细介绍，请读者参考笔者的旧作《变分自编码器（一）：原来是这么一回事》、《变分自编码器（二）：从贝叶斯观点出发》等。

VAE的训练流程 #

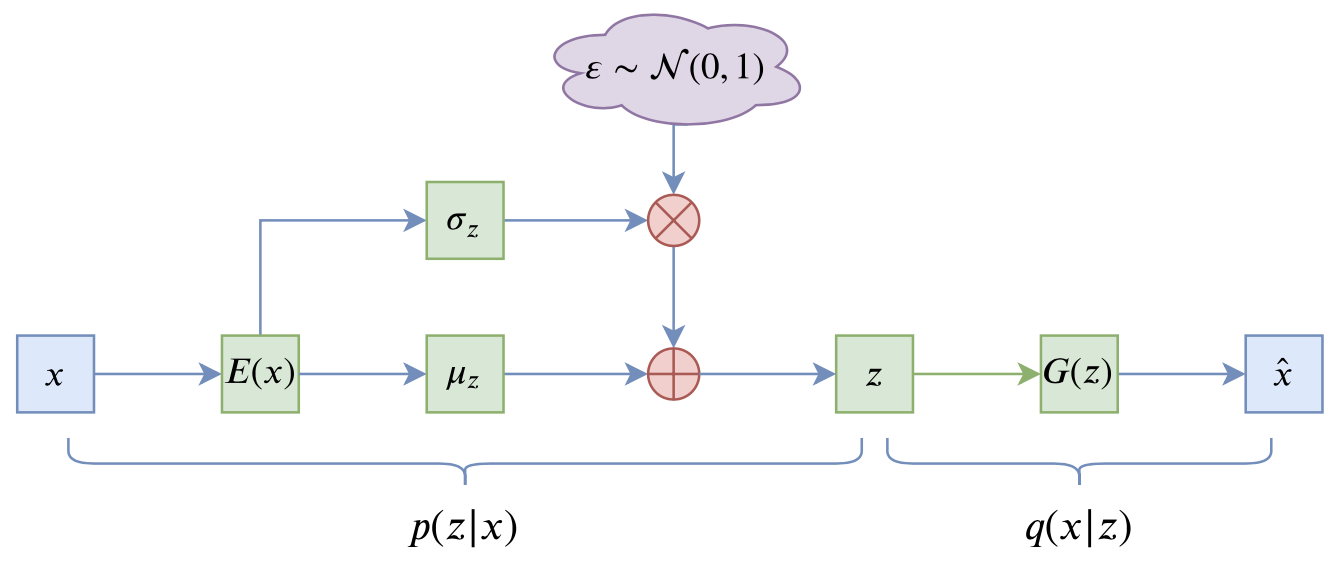
VAE的训练流程大概可以图示为

VAE训练流程图示

写成公式就是
$$\begin{equation}\mathcal{L} = \mathbb{E}_{x\sim \tilde{p}(x)} \Big[\mathbb{E}_{z\sim p(z|x)}\big[-\log q(x|z)\big]+KL\big(p(z|x)\big\Vert q(z)\big)\Big]
\end{equation}$$
其中第一项就是重构项，$\mathbb{E}_{z\sim p(z|x)}$是通过重参数来实现；第二项则称为KL散度项，这是它跟普通自编码器的显式差别，如果没有这一项，那么基本上退化为常规的AE。更详细的符号含义可以参考《变分自编码器（二）：从贝叶斯观点出发》。

NLP中的VAE #

在NLP中，句子被编码为离散的整数ID，所以$q(x|z)$是一个离散型分布，可以用万能的“条件语言模型”来实现，因此理论上$q(x|z)$可以精确地拟合生成分布，问题就出在$q(x|z)$太强了，训练时重参数操作会来噪声，噪声一大，$z$的利用就变得困难起来，所以它干脆不要$z$了，退化为无条件语言模型（依然很强），$KL(p(z|x)\Vert q(z))$则随之下降到0，这就出现了KL散度消失现象。

这种情况下的VAE模型并没有什么价值：KL散度为0说明编码器输出的是常数向量，而解码器则是一个普通的语言模型。而我们使用VAE通常来说是看中了它无监督构建编码向量的能力，所以要应用VAE的话还是得解决KL散度消失问题。事实上从2016开始，有不少工作在做这个问题，相应地也提出了很多方案，比如退火策略、更换先验分布等，读者Google一下“KL Vanishing”就可以找到很多文献了，这里不一一溯源。

BN的巧与妙 #

本文的方案则是直接针对KL散度项入手，简单有效而且没什么超参数。其思想很简单：

KL散度消失不就是KL散度项变成0吗？我调整一下编码器输出，让KL散度有一个大于零的下界，这样它不就肯定不会消失了吗？

这个简单的思想的直接结果就是：在$\mu$后面加入BN层，如图

往VAE里加入BN

推导过程简述 #

为什么会跟BN联系起来呢？我们来看KL散度项的形式：
\begin{equation}\mathbb{E}_{x\sim\tilde{p}(x)}\left[KL\big(p(z|x)\big\Vert q(z)\big)\right] = \frac{1}{b} \sum_{i=1}^b \sum_{j=1}^d \frac{1}{2}\Big(\mu_{i,j}^2 + \sigma_{i,j}^2 - \log \sigma_{i,j}^2 - 1\Big)\end{equation}
上式是采样了$b$个样本进行计算的结果，而编码向量的维度则是$d$维。由于我们总是有$e^x \geq x + 1$，所以$\sigma_{i,j}^2 - \log \sigma_{i,j}^2 - 1 \geq 0$，因此
\begin{equation}\mathbb{E}_{x\sim\tilde{p}(x)}\left[KL\big(p(z|x)\big\Vert q(z)\big)\right] \geq \frac{1}{b} \sum_{i=1}^b \sum_{j=1}^d \frac{1}{2}\mu_{i,j}^2 = \frac{1}{2}\sum_{j=1}^d \left(\frac{1}{b} \sum_{i=1}^b \mu_{i,j}^2\right)\label{eq:kl}\end{equation}
留意到括号里边的量，其实它就是$\mu$在batch内的二阶矩，如果我们往$\mu$加入BN层，那么大体上可以保证$\mu$的均值为$\beta$，方差为$\gamma^2$（$\beta,\gamma$是BN里边的可训练参数），这时候
\begin{equation}\mathbb{E}_{x\sim\tilde{p}(x)}\left[KL\big(p(z|x)\big\Vert q(z)\big)\right] \geq \frac{d}{2}\left(\beta^2 + \gamma^2\right)\label{eq:kl-lb}\end{equation}
所以只要控制好$\beta,\gamma$（主要是固定$\gamma$为某个常数），就可以让KL散度项有个正的下界，因此就不会出现KL散度消失现象了。这样一来，KL散度消失现象跟BN就被巧妙地联系起来了，通过BN来“杜绝”了KL散度消失的可能性。

为什么不是LN？ #

善于推导的读者可能会想到，按照上述思路，如果只是为了让KL散度项有个正的下界，其实LN（Layer Normalization）也可以，也就是在式$\eqref{eq:kl}$中按$j$那一维归一化。

那为什么用BN而不是LN呢？

这个问题的答案也是BN的巧妙之处。直观来理解，KL散度消失是因为$z\sim p(z|x)$的噪声比较大，解码器无法很好地辨别出$z$中的非噪声成分，所以干脆弃之不用；而当给$\mu(x)$加上BN后，相当于适当地拉开了不同样本的$z$的距离，使得哪怕$z$带了噪声，区分起来也容易一些，所以这时候解码器乐意用$z$的信息，因此能缓解这个问题；相比之下，LN是在样本内进的行归一化，没有拉开样本间差距的作用，所以LN的效果不会有BN那么好。

进一步的结果 #

事实上，原论文的推导到上面基本上就结束了，剩下的都是实验部分，包括通过实验来确定$\gamma$的值。然而，笔者认为目前为止的结论还有一些美中不足的地方，比如没有提供关于加入BN的更深刻理解，倒更像是一个工程的技巧，又比如只是$\mu(x)$加上了BN，$\sigma(x)$没有加上，未免有些不对称之感。

经过笔者的推导，发现上面的结论可以进一步完善。

联系到先验分布 #

对于VAE来说，它希望训练好后的模型的隐变量分布为先验分布$q(z)=\mathcal{N}(z;0,1)$，而后验分布则是$p(z|x)=\mathcal{N}(z; \mu(x),\sigma^2(x))$，所以VAE希望下式成立：
\begin{equation}q(z) = \int \tilde{p}(x)p(z|x)dx=\int \tilde{p}(x)\mathcal{N}(z; \mu(x),\sigma^2(x))dx\end{equation}
两边乘以$z$，并对$z$积分，得到
\begin{equation}0 = \int \tilde{p}(x)\mu(x)dx=\mathbb{E}_{x\sim \tilde{p}(x)}[\mu(x)]\end{equation}
两边乘以$z^2$，并对$z$积分，得到
\begin{equation}1 = \int \tilde{p}(x)\left[\mu^2(x) + \sigma^2(x)\right]dx = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\mu^2(x)\right] + \mathbb{E}_{x\sim \tilde{p}(x)}\left[\sigma^2(x)\right]\end{equation}
如果往$\mu(x),\sigma(x)$都加入BN，那么我们就有
\begin{equation}\begin{aligned}
&0 = \mathbb{E}_{x\sim \tilde{p}(x)}[\mu(x)] = \beta_{\mu}\\
&1 = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\mu^2(x)\right] + \mathbb{E}_{x\sim \tilde{p}(x)}\left[\sigma^2(x)\right] = \beta_{\mu}^2 + \gamma_{\mu}^2 + \beta_{\sigma}^2 + \gamma_{\sigma}^2
\end{aligned}\end{equation}
所以现在我们知道$\beta_{\mu}$一定是0，而如果我们也固定$\beta_{\sigma}=0$，那么我们就有约束关系：
\begin{equation}1 = \gamma_{\mu}^2 + \gamma_{\sigma}^2\label{eq:gamma2}\end{equation}

参考的实现方案 #

经过这样的推导，我们发现可以往$\mu(x),\sigma(x)$都加入BN，并且可以固定$\beta_{\mu}=\beta_{\sigma}=0$，但此时需要满足约束$\eqref{eq:gamma2}$。要注意的是，这部分讨论还仅仅是对VAE的一般分析，并没有涉及到KL散度消失问题，哪怕这些条件都满足了，也无法保证KL项不趋于0。结合式$\eqref{eq:kl-lb}$我们可以知道，保证KL散度不消失的关键是确保$\gamma_{\mu} > 0$，所以，笔者提出的最终策略是：
\begin{equation}\begin{aligned}
&\beta_{\mu}=\beta_{\sigma}=0\\
&\gamma_{\mu} = \sqrt{\tau + (1-\tau)\cdot\text{sigmoid}(\theta)}\\
&\gamma_{\sigma} = \sqrt{(1-\tau)\cdot\text{sigmoid}(-\theta)}
\end{aligned}\end{equation}
其中$\tau\in(0,1)$是一个常数，笔者在自己的实验中取了$\tau=0.5$，而$\theta$是可训练参数，上式利用了恒等式$\text{sigmoid}(-\theta) = 1-\text{sigmoid}(\theta)$。

关键代码参考（Keras）：

class Scaler(Layer):
    """特殊的scale层
    """
    def __init__(self, tau=0.5, **kwargs):
        super(Scaler, self).__init__(**kwargs)
        self.tau = tau

    def build(self, input_shape):
        super(Scaler, self).build(input_shape)
        self.scale = self.add_weight(
            name='scale', shape=(input_shape[-1],), initializer='zeros'
        )

    def call(self, inputs, mode='positive'):
        if mode == 'positive':
            scale = self.tau + (1 - self.tau) * K.sigmoid(self.scale)
        else:
            scale = (1 - self.tau) * K.sigmoid(-self.scale)
        return inputs * K.sqrt(scale)

    def get_config(self):
        config = {'tau': self.tau}
        base_config = super(Scaler, self).get_config()
        return dict(list(base_config.items()) + list(config.items()))


def sampling(inputs):
    """重参数采样
    """
    z_mean, z_std = inputs
    noise = K.random_normal(shape=K.shape(z_mean))
    return z_mean + z_std * noise


e_outputs  # 假设e_outputs是编码器的输出向量
scaler = Scaler()
z_mean = Dense(hidden_dims)(e_outputs)
z_mean = BatchNormalization(scale=False, center=False, epsilon=1e-8)(z_mean)
z_mean = scaler(z_mean, mode='positive')
z_std = Dense(hidden_dims)(e_outputs)
z_std = BatchNormalization(scale=False, center=False, epsilon=1e-8)(z_std)
z_std = scaler(z_std, mode='negative')
z = Lambda(sampling, name='Sampling')([z_mean, z_std])

文章内容小结 #

本文简单分析了VAE在NLP中的KL散度消失现象，并介绍了通过BN层来防止KL散度消失、稳定训练流程的方法。这是一种简洁有效的方案，不单单是原论文，笔者私下也做了简单的实验，结果确实也表明了它的有效性，值得各位读者试用。因为其推导具有一般性，所以甚至任意场景（比如CV）中的VAE模型都可以尝试一下。

转载到请包括本文地址：https://kexue.fm/archives/7381

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。